다리를 지나는 트럭
문제 설명
트럭 여러 대가 강을 가로지르는 일차선 다리를 정해진 순으로 건너려 합니다. 모든 트럭이 다리를 건너려면 최소 몇 초가 걸리는지 알아내야 합니다. 다리에는 트럭이 최대 bridge_length대 올라갈 수 있으며, 다리는 weight 이하까지의 무게를 견딜 수 있습니다. 단, 다리에 완전히 오르지 않은 트럭의 무게는 무시합니다.
예를 들어, 트럭 2대가 올라갈 수 있고 무게를 10kg까지 견디는 다리가 있습니다. 무게가 [7, 4, 5, 6]kg인 트럭이 순서대로 최단 시간 안에 다리를 건너려면 다음과 같이 건너야 합니다.
| 경과 시간 | 다리를 지난 트럭 | 다리를 건너는 트럭 | 대기 트럭 |
|---|---|---|---|
| 0 | [] | [] | [7,4,5,6] |
| 1~2 | [] | [7] | [4,5,6] |
| 3 | [7] | [4] | [5,6] |
| 4 | [7] | [4,5] | [6] |
| 5 | [7,4] | [5] | [6] |
| 6~7 | [7,4,5] | [6] | [] |
| 8 | [7,4,5,6] | [] | [] |
따라서, 모든 트럭이 다리를 지나려면 최소 8초가 걸립니다.
solution 함수의 매개변수로 다리에 올라갈 수 있는 트럭 수 bridge_length, 다리가 견딜 수 있는 무게 weight, 트럭 별 무게 truck_weights가 주어집니다. 이때 모든 트럭이 다리를 건너려면 최소 몇 초가 걸리는지 return 하도록 solution 함수를 완성하세요.
제한 조건
bridge_length는 1 이상 10,000 이하입니다.
weight는 1 이상 10,000 이하입니다.
truck_weights의 길이는 1 이상 10,000 이하입니다.
모든 트럭의 무게는 1 이상 weight 이하입니다.
입출력 예
| bridge_length | weight | truck_weights | return |
|---|---|---|---|
| 2 | 10 | [7,4,5,6] | |
| 100 | 100 | [10] | 101 |
| 100 | 100 | [10,10,10,10,10,10,10,10,10,10] | 110 |
풀이
이 문제는 트럭이 1씩 움직인다는 것을 알아야 풀 수 있다. (문제에 말이 없어서 고생 쫌 했다)
문제 설명 예시를 다시 정리하자면 아래 표와 같다.
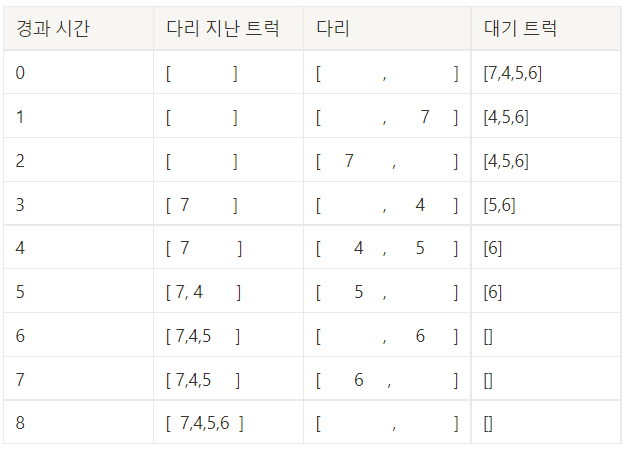
다리 길이 만큼 트럭이 1씩 전진하는 것!
예시) bridge_length = 100, weight = 100, truck_weights = [10]
위 예시로 해석해 보자면, "최대 100kg의 무게를 버틸 수 있는", "길이가 100인 다리"가 있는데 "10kg의 트럭이 한대 지나는데 최소 몇 초"가 걸리냐 를 찾아야 한다.
답이 101초인 이유는
길이가 100인 다리를 10kg의 트럭 한대가 지나는데 1초에 1씩 움직이므로, 다리를 시작부터 끝까지 가는데 100초가 걸린다. 그리고 다리를 나가는데 1초가 걸려 100초 + 1초 => 101초가 최소 시간이란 것이다.
계속 테스트케이스 틀리길래... 질문하기에서 빈 공간을 무게가 0인 트럭이라고 생각하라는 힌트를 얻었다...ㄳㄳ
_
"트럭이 올라가지 못하는 다리 공간을 0으로 채우기! "
이게 핵심 포인트이다.
예를 들어, 최대 100kg 무게를 버틸 수 있는 길이가 5인 다리를 트럭 100kg, 60kg, 40kg이 올라가야한다 가정해보자.
0초 ㅡ 다리 = [ 0, 0, 0, 0, 0] sum(다리) = 0 kg
1초 ㅡ 다리 = [ 0, 0, 0, 0, 100] 이다. sum(다리) = 100kg
최대 100kg만 올라갈 수 있으므로, 만약 2초에 60kg이 올라간다면 100kg을 초과하므로 100kg이 다리를 빠져나갈 때 까지 기다려야한다.
2초 ㅡ 다리 = [0, 0, 0, 100, 0] sum(다리) = 100kg
3초 ㅡ 다리 = [0, 0, 100, 0, 0] sum(다리) = 100kg
4초 ㅡ 다리 = [0, 100, 0, 0, 0] sum(다리) = 100kg
5초 ㅡ 다리 = [100, 0, 0, 0, 0] sum(다리) = 100kg
6초에는 100이 빠져나가고, sum(다리) = 0 이므로, 60kg 트럭이 오를 수 있다.
(이렇게 뒤에 공간을 0으로 채운다면, 다리의 길이를 계속 bridge_length로 유지할 수 있다. )
6초 ㅡ 다리 = [0, 0, 0, 0, 60] sum(다리) = 60kg
7초에 sum(다리) + 40kg = 100kg이므로, 40kg이 오를 수 있다.
7초 ㅡ 다리 = [0, 0, 0, 60, 40] sum(다리) = 100kg
대기하는 트럭이 더 이상 없을 때 즉, 마지막 트럭이 시작에 있을 때, 마지막 트럭이 빠져나가는 시간만 계산해주면 된다.
마지막 트럭이 빠져나가는 시간은 항상 다리 길이와 동일하다.
따라서 7초 + 5초 = 12초가 최소 시간이다 !
코드 구현
from collections import deque
def solution(bridge_length, weight, truck_weights):
q = deque([0]*bridge_length)
total_time = 0 # 걸리는 total 시간
qSum = 0 # 다리 weight
while truck_weights:
qSum -= q.popleft() # 빠져나온 트럭 무게 제거
total_time+=1 # 트럭은 1씩 움직이므로, while문이 돌아가는 시간 만큼 time 추가
if (qSum + truck_weights[0])>weight: # 현재 다리 weight + 다음 트럭 무게가 weight를 넘으면
q.append(0) # 다리에 다음 트럭 올라갈 수 없으므로 0을 추가
else:# 다음 트럭이 올라갈 수 있으면
next = truck_weights.pop(0) # 다음 트럭 나옴
qSum += next # 다음 트럭 무게 추가
q.append(next) # 다음 트럭 queue에 추가
return total_time + len(q) # 다리를 빠져오지 못한 트럭 + total 시간 