Weight Initialization

• 논문을 볼 때 혹은 코드를 구현해서 모델링할 때 종종 가중치를 사용

• 보통 임베딩 어텐션 연산에 사용되기도 하고 학습의 대상이 되기도 한다.

• 오늘은 대표적인 가중치 초기화 방법인 Xavier와 Kaiming 방법에 대해 정리해보자!

---

Initialization Method

1) Xavier

• xavier는 2010년에 Xavier Glorot와 Yoshua Bengio가 제안한 방식으로,

• 출력 레이어의 분산이 입력 레이어의 분산과 동일해야 한다.는 원리에 기반한다.

• Xavier 방법은 입력 노드 수와 툴력 노드 수를 모두 고려한다.

• 가중치의 분산은 아래 값을 가지며
  $a = \sqrt{\frac{2}{n_{in} + n_{out}}}$

  입/출력 노드가 모두 관여함을 알 수 있다.

• 또한 가중치 초기화 시 두 형태 분포가 사용된다.

  • Uniform(균둥분포)
  • Normal(정규분포)

• Uniform(균둥분포)

  • [-a, +a]의 직사각형의 분포를 보인다.

  • 균등 분포에서, 분산 공식은 $\frac{L^2}{12}$` 이며, $L$은 가로 길이를 의미하므로 $2a$

  • 따라서, 표준편차는 $\frac{a}{\sqrt{3}}$이므로

  • 최종 범위
    $-\sqrt{3 \times \frac{2}{in+out}}$ ~ $+\sqrt{3 \times \frac{2}{in+out}}$

• Normal(정규분포)

  • 종 모양의 분포를 이루며
  • 분포의 표준편차는
    $-\sqrt{\frac{2}{in+out}}$ ~ $\sqrt{\frac{2}{in+out}}$

• 균등 분포는 데이터가 중심에 밀집되지 않고 전체 구간에 고르게 퍼져 있기 때문에 정규 분포와 동일한 분산을 가지려면$\sqrt{3}$배 더 넓은 범위를 가져야 하는 특성 때문에 두 분포의 범위가 다른 특징을 갖는다.

• sigmoid,Tanh 활성화 함수와 같이 사용
  • xavier는 0 근처에 값이 몰려 있는 형태인데, 두 함수는 0 근처에서 거의 직선에 가까운 형태를 가져, 데이터를 통과시켜도 신호의 분산이 안정적으로 유지되기 때문
  • 이는 학습 초기 기울기 소실 방지 하나, 신경망이 깊은 경우에는 오히려 기울기 소실을 유발하니 주의!

2) Kaiming(He)

• kaiming(또는 He) 초기화는 2015년에 제안된 방법으로,

• Xavier + ReLU 사용 단점을 보완하기 위해 제안된 방법

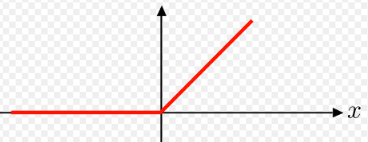
  • ReLU

• ReLU는 음수를 모두 0으로 지워버리기 때문에 한 레이어를 지날 때마다 신호의 분산이 절반씩 줄어들어, 10개 레이어만 지나도 $2^{10}$만큼 줄어들어, 학습 자체가 안 되는 문제 발생

• 위 문제를 해결하기 위한 He 초기화 방법은 단순하다.

  • 통과되면 줄어드는 신호를 사전에 방지하기 위해 초기화 시 애초에 2배씩 크게 초기화하여 깊은 신경망의 분산 손실 방지

• Xavier와 달리 입력 노드 개수만 고려하여 초기화 범위를 지정한다.

  • $a = \sqrt{\frac{2}{n_{in}}}$

• Uniform(균둥분포)

  • xavier와 유사하며
  • 최종 범위
    $-\sqrt{3 \times \frac{2}{in}}$ ~ $+\sqrt{3 \times \frac{2}{in}}$

• Normal(정규분포)

  • 종 모양의 분포를 이루며
  • 분포의 표준편차는
    $-\sqrt{\frac{2}{in}}$ ~ $\sqrt{\frac{2}{in}}$

---

정리

Xavier	Kaiming(He)
입/출력 크기 모두 고려	입력 크기만 고려
깊은 신경망에서 기울기 소실 발생	깊은 신경망에 적합
Sigmoid, Tanh와 조합	ReLU, LeakyReLU와 조합
$a = \sqrt{\frac{6}{in+out}}$ (uniform)	$a = \sqrt{\frac{6}{in}}$ (uniform)
$a = \sqrt{\frac{2}{in+out}}$ (normal)	$a = \sqrt{\frac{2}{in}}$ (normal)