[PS 백준 - 5.9] 1890번: 점프

문제 정보

백준 1890번 - 바로가기

• 난이도: 실버 2
• 알고리즘: 다이나믹 프로그래밍

---

코멘트

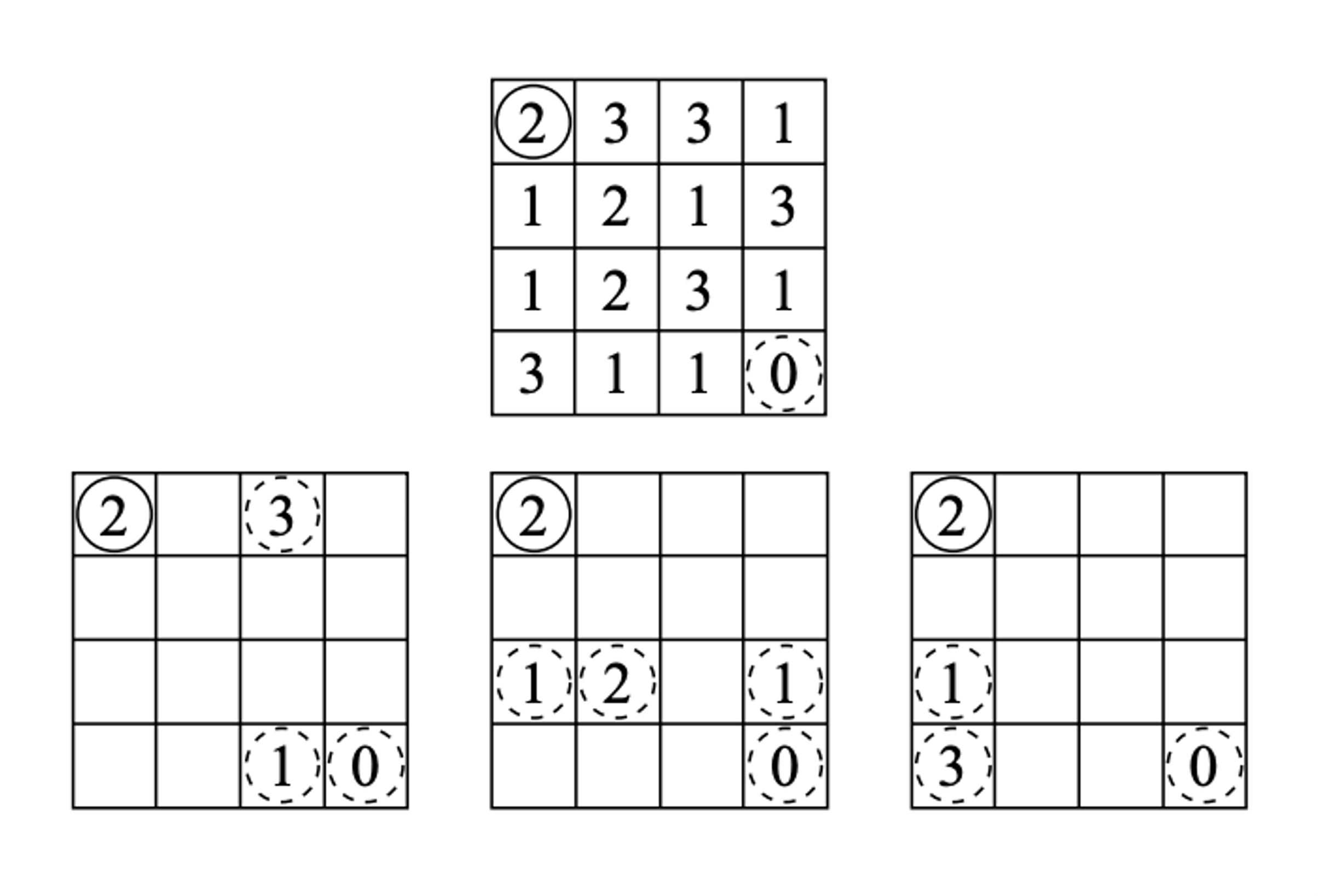
이 문제도 Moo 게임과 같이 수개월간 틀렸었던 문제다. 예전에 풀었을 때는 DP의 개념을 몰라서 메모이제이션을 하지 않아 시간 초과가 계속 떴었다.

• [Parameters]
  • r: 행 좌표 (row)
  • c: 열 좌표 (col)
    - n: 해당 좌표에 적힌 숫자
• [base case]
  • 목적지에 도착하면 1 리턴
    - n이 0이거나 좌표가 맵을 벗어날 경우 0 리턴
• [Logic]
  1. 매 좌표에 적힌 숫자마다 오른쪽으로 간 경우와 아래쪽으로 간 경우의 함수를 호출한다.
  2. 재귀적으로 좌표가 이동하다가 목적지를 만나면 1을 리턴하므로 최종적으로는 모든 목적지의 수가 더해져서 리턴된다.

주의사항!!

• 경로의 개수는 $2^{63}-1$보다 작거나 같다.
  
  → 출력 조건 함정에 조심!! 8 byte 크기의 자료형이 필요하다.

---

소스 코드

<탑다운 방식>

#include <iostream>
#include <cstdio>
#include <string>
#include <cmath>
#include <vector>
#include <set>
#include <list>
#include <stack>
#include <queue>
#include <map>
#include <algorithm>

#define MAX 101

using namespace std;

int maps[MAX][MAX];
long long int dp[MAX][MAX];
int N;

// r, c는 좌표 / n은 적힌 숫자
long long int jump(int r, int c, int n) {
	// cout << "(" << r << "," << c << ") n: " << n << endl;
	// base case
	if (r == N - 1 && c == N - 1) return 1;
	if (n == 0 || r > N - 1 || c > N - 1) return 0;

	// memoization
	if (dp[r][c] != -1) return dp[r][c];

	long long int result = jump(r + n, c, maps[r + n][c]) + jump(r, c + n, maps[r][c + n]);
	dp[r][c] = result;
	return result;
}

int main() {
	std::ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

	cin >> N;
	fill(&dp[0][0], &dp[MAX - 1][MAX], -1);
	
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			int x;
			cin >> x;
			maps[i][j] = x;
		}
	}
	dp[N - 1][N - 1] = 1;

	// 스타트: jump(0, 0, map[0][0]);
	cout << jump(0, 0, maps[0][0]);

}

---

<바텀업 방식> - by zzoni

#include <iostream>
#include <algorithm>
using namespace std;

int map[101][101];
long long int dp[101][101]; // dp에 경로개수 저장!
int N;

int main() {
    std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> N;

    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            cin >> map[i][j];
        }
    }

    dp[0][0] = 1; // 시작점은 무조건 1번 거치니까

    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (map[i][j] != 0 ){ // 종착지가 아니라면
                //아래로
                if (i + map[i][j] < N) {
                    dp[i + map[i][j]][j] += dp[i][j];
                }
                //오른쪽으로
                if (map[i][j] != 0 && j + map[i][j] < N) {
                    dp[i][j + map[i][j]] += dp[i][j];
                }
            }
        }
    }

    cout << dp[N - 1][N - 1];

    return 0;
}