https://school.programmers.co.kr/learn/courses/30/lessons/118667
문제
문제 이해
- 길이가 같은 두 개의 queue
- 하나의 queue (pop) -> 다른 queue (insert)
- 목적: 각 큐의 원소 합이 서로 같도록 한다.
- 구해야 하는 것 : 필요한 작업의 "최소 횟수"
- 작업 1번 : pop + insert
- 문제에서는 큐를 "배열"로 표현한다 -> 작은 index 일 수록 먼저 집어넣은 것
- 두 개의 큐가 주어지면
- 각 큐의 원소의 합이 되어야 하는 값 : 두 큐의 모든 원소의 합 / 2
문제 풀이
일단 첫 번째 생각은 틀렸었다 ㅋㅋ...
이래서 예시까지 모두 읽어보고 풀이를 시작해야하는 것 같다
나는 고정된 큐만을 생각하고 있었다. 그래서 " 맨 처음의 큐의 상태" 를 기반으로 누적합을 사용하는 것을 생각했었다.
그리고, insert, pop 이후 두 큐의 길이가 같아야 한다고도 생각하고 있었다... (아님)
그런데 이렇게 하면, 동적으로 변하는 큐를 고려하지 않게 되는 문제가 존재한다.
[1,2,1,2]
[1,10,1,2] 가 있는 경우 -> 총합 : 6 + 11 + 3 = 20 이다
->
[] 다(4) pop 해서 q2 에 insert
[1,10,1,2,1,2,1,2]
->
[1] q2 에서 하나 pop 해 옴 (5)
[10,1,2,1,2,1,2]
->
[1,10] q2 에서 하나 Pop 해옴 (6)
[1,2,1,1,2,1,2]
->
[10] q2 로 하나 insert 함 (7)
[1,2,1,1,2,1,2,1]
문제 풀이 변경
q1, q2 를 이어 붙여, 합이 2/A 인 특정 수열을 구하는 것으로 생각해 봐야 한다.그런데 이걸 어떻게 구해야하는 건지 생각이 안났다.. idx 가 0인 때부터 차례차례 다 해봐야 하나 생각했다. 이렇게 하면 30만 x 30만 가지 경우의 수가 나와서 시간초과가 나올 것이 분명하다.분명 이런 상황('\~ 인 것을 구하기')과 비슷한 문제를 예전에 풀어 본 기억이 있었다 -> 투 포인터를 사용해 보자~~아... 생각해보니, 투 포인터를 할 경우, sum 이 특정값인 경우도 많이 존재한다. 각 경우들에서 최소횟수를 만들어내는 경우를 또 찾아내야한다 ㅠㅠㅠ..심지어 투 포인터에서도 , sum 이 A/2 인 여러 경우들을 찾는 것을 고려해야하는데, 이러면 또 경우의수 (left 를 움직이냐 right 를 움직이냐) 가 엄청 많아진다.. 이렇게 푸는 것은 아닌 것 같다.
- 동적으로 변경되는 것 까지 모두 고려 되기 위해서는, 직접 push pop 해보는 것 밖에 없는 거 아닐까..???
- 복잡하게 생각한 것이 문제인 것 같기도 하다.
두 큐의 총합을 구해 이것을 A 라고 칭한다.
“최소 횟수" 라는 것이 걸렸었는데
어차피 A/2 보다 작으면 원소를 받아야지만 A/2 가 될 수 있다.
어차피 A/2 보다 크면 원소를 보내줘야 한다.
그리고 이 문제는 queue 라서 한 곳으로만 빼고, 한 곳으로만 받을 수 있어서, 그냥 A/2 보다 작으면 추가하고, 크면 빼는 식으로 생각해도 될 문제였다.
즉, Greedy 문제였다.
실제 Queue 에서 넣었다 뺐다 하기엔 뭔가 불안해서
위에서 생각했던 것 처럼 q1, q2 를 이어 붙여 사용하는 것으로 생각했다.
그리고 index 만을 사용하는 것이다. → 하나의 거대한 circular queue 처럼 생각하면 된다.
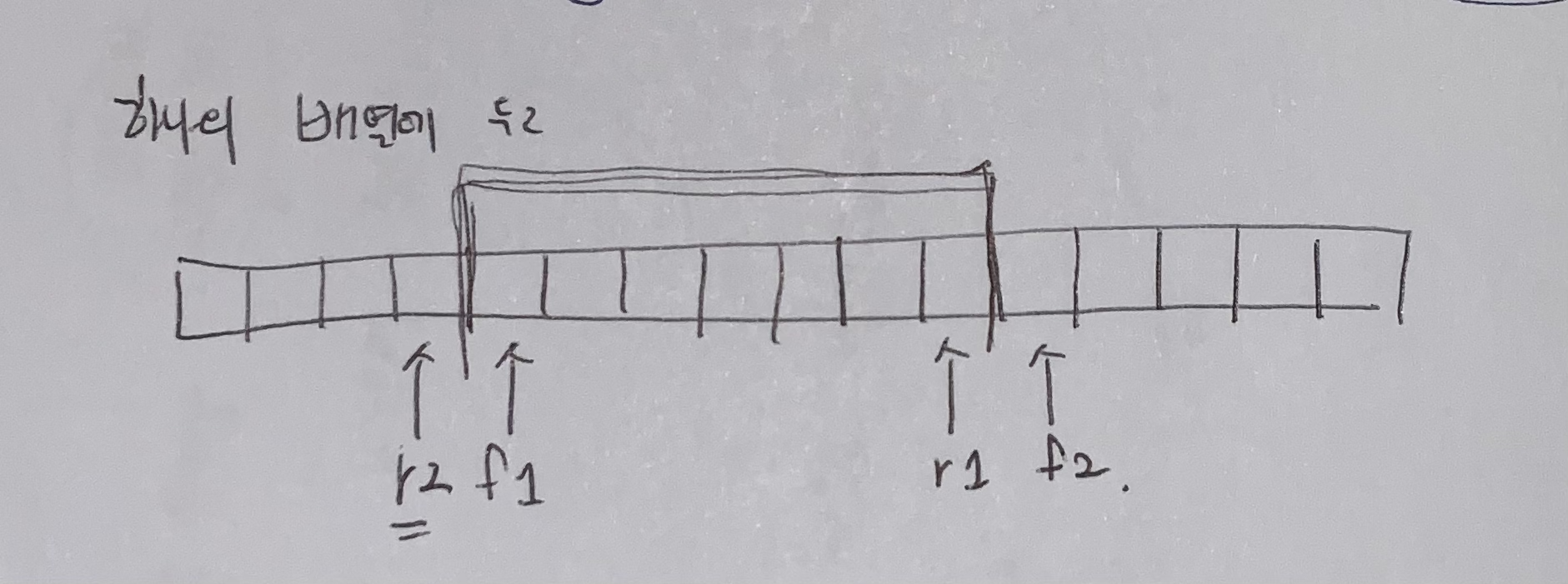
따라서 아래와 같이 하면 될 것 같다.
q1 에는 f1(front), r1(rear) 포인터를 갖고
q2 는 f2(front), r2(rear) 포인터를 갖는다
q1 을 기준으로만 한다.
- q1 이 A/2 보다 더 작은 경우
- r1 = (r1+1)%len
- f2 = (f2+1)%len
- q2 이 A/2 보다 더 큰 경우
- f1 = (f1+1)%len
- r2 = (r2+1)%len
하지만 이 경우, 불가능한 경우에는 “무한 반복" 을 하게 되기 때문에 “횟수 제한" 을 둬야 한다.
- 💥 개인적으로 “횟수제한" 에서 막혔었다…. → 이거를 제대로 안하면 case 1 에서 계속 실패하게 된다.
나는 각 큐 모두 한 번씩 다 이동된 횟수 → 즉, q1.len*2 면 충분하다고 생각했었다.
그런데 다음과 같은 경우가 존재한다. (🐳 반례의 중요성..!!)
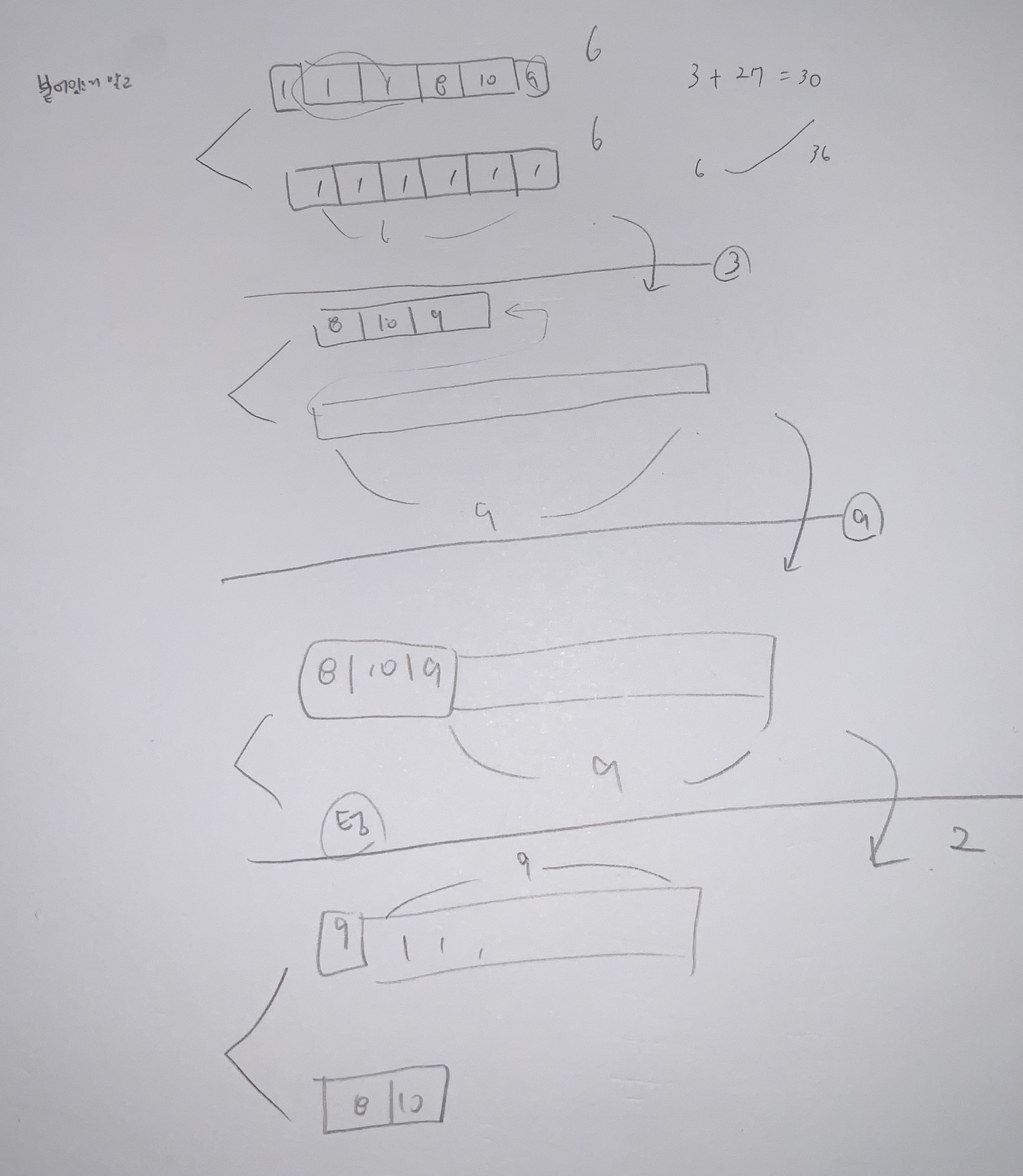
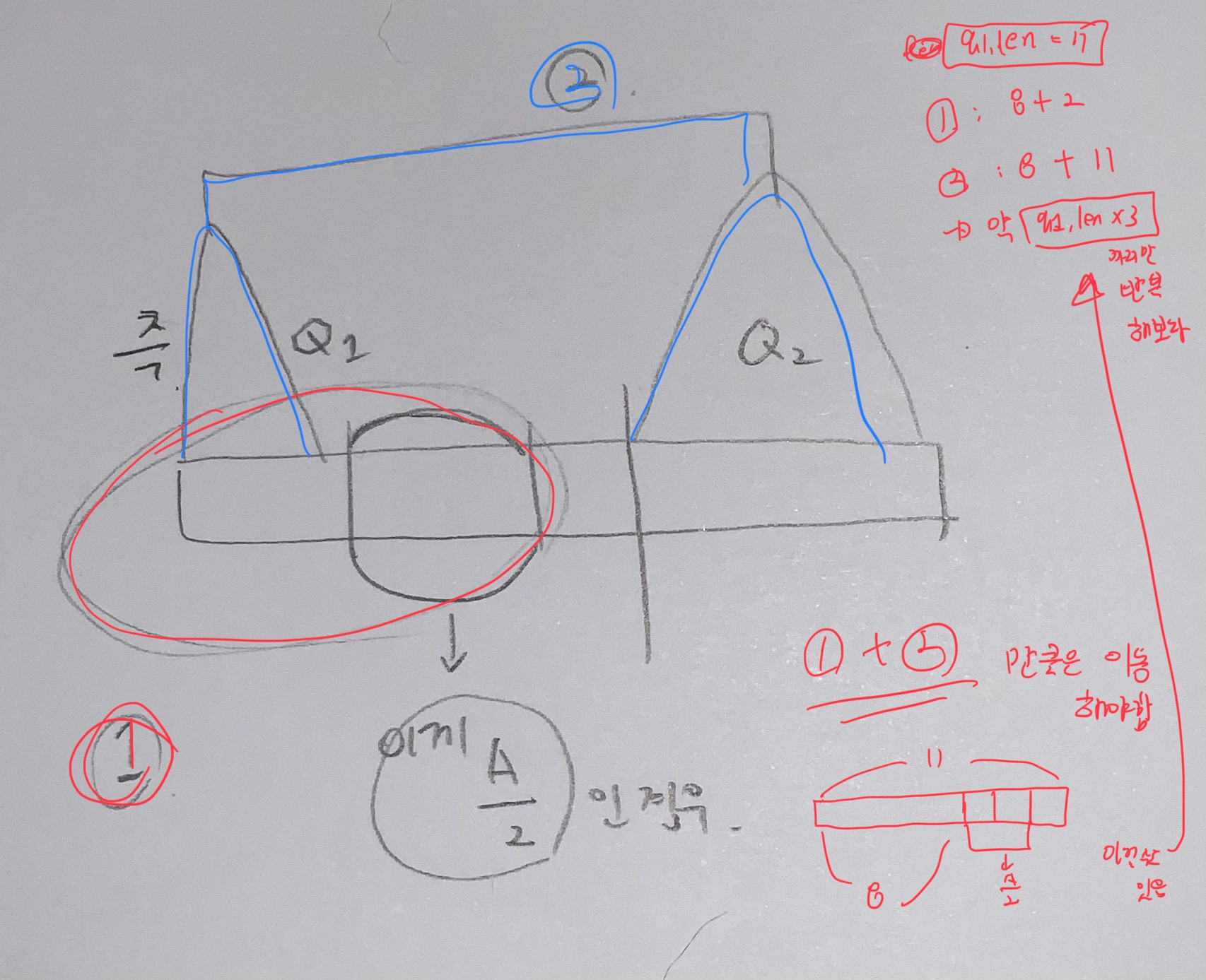
따라서 q.len*3 까지만 반복하도록 한다.
이 “반복 횟수" 는 무한 루프를 돌아서 시간초과가 나는 것을 방지하는 용도 이기 때문에, 일정 수 이상의 값으로만 limit 을 주면돼서, 사실 명확하게 q.len*3 이 아닐 수도 있다. 이보다 작은 값의 limit 일 수도 있음.
class Solution {
public int solution(int[] queue1, int[] queue2) {
int answer = -2;
int len = queue1.length + queue2.length;
int[] total = concatenate(queue1,queue2,len);
long s1 = sum(queue1);
long s = sum(total);
if(s % 2 != 0) { // 총 합이 홀 수라면 두 큐의 합이 같아 질 수 없다
return -1;
}
answer = search(total, 0, queue1.length, queue1.length-1, len-1, s/2, s1);
return answer;
}
// 두 큐 를 길게 이어 붙인 결과를 리턴한다
private int[] concatenate(int[] q1, int[] q2, int len) {
int[] total = new int[len];
for(int i =0; i< q1.length; i++) {
total[i] = q1[i];
total[q1.length + i] = q2[i];
}
return total;
}
private int search(int[] arr, int front1, int front2, int rear1, int rear2, long target, long curSum) {
int f1 = front1; int f2 = front2;
int r1 = rear1; int r2 = rear2;
long s = curSum;
int len = arr.length; // 작업 횟수는 len 미만이어야 한다.
int cnt = 0;
boolean fail = true;
while(cnt <= (len + len / 2)) {
if(s == target) {
fail = false;
break;
}
else if ( s < target ) {
r1 = (r1 + 1) % len;
f2 = (f2 + 1) % len;
s += arr[r1];
cnt++;
} else {
s -= arr[f1];
f1 = (f1 + 1) % len;
r2 = (r2 + 1) % len;
cnt++;
}
}
if(fail) return -1;
return cnt;
}
private long sum(int[] arr) {
int len = arr.length;
long sum = 0;
for (long numb : arr) {
sum += numb;
}
return sum;
}
}