[동빈나]최단경로 : 플로이드 워셜 알고리즘

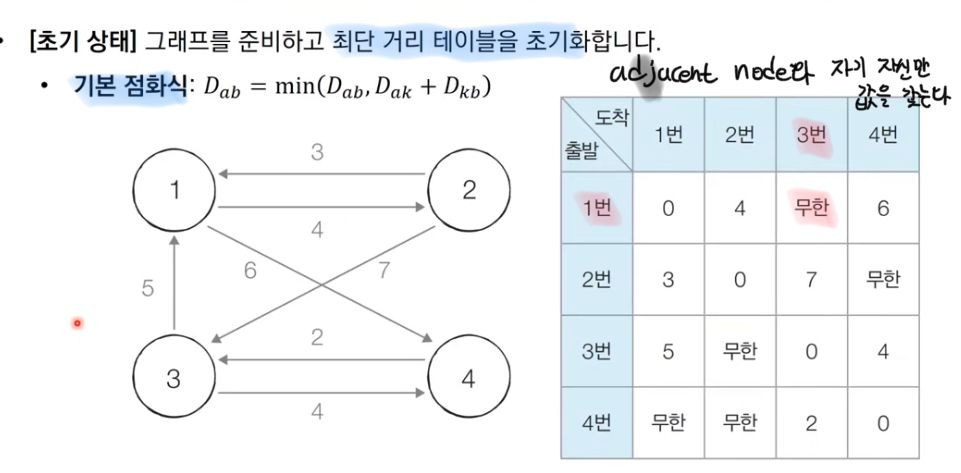
• [***모든 노드에서 다른 모든 노드까지]***의 최단 경로를 모두 계산한다.
• Floyd - Warshall 알고리즘은 다익스트라 알고리즘과 마찬가지로 “단계별로 거쳐가는 노드를 기준”으로 알고리즘을 수행한다.
  • 다만, 매 단계마다, “방문하지 않은 노드 중” “최단 거리를 갖는 노드 찾기” 과정이 필요하지는 않다.
• 2D 테이블에, [최단 거리 정보]를 저장한다.
  • 왜냐하면 [모든 노드] —> [모든 노드] 까지의 최단 경로를 모두 탐색해야 하기 때문임.
  • [다익스트라] 의 경우는, [ 1D table상에서, 가장 최소 값인 노드를 뽑아] 서, [그래프 정보를 활용] 하였던 것과 다르다.
• DP 유형에 속한다. (??)
  • 2차원 테이블에 기록되어있는 값을 점화식에 따라서 갱신한다는 점에서 다이나믹 프로그래밍에 속한다.
  • 점화식에 맞게 3중 반복문을 이용해서 2차원 테이블을 갱신해주는 방식으로 동작한다.
• 구현난이도는 다익스트라 알고리즘보다 쉬운 편.
• 모든 노드 →다른 노드까지의 최단 거리 구하는 과정에서 시간복잡도는 O(n^3)이다.
  • 따라서 노드의 개수가 적은 과정에서 효과적으로 사용가능.
  • 노드개수 , 간선개수 많은 경우는 다익스트라 알고리즘 사용할 것

• 특정한 노드를 거쳐갈 때를 기준으로 한다는 점에서 다익스트라 알고리즈과 유사성이 있다.
  • 다만 이때, [a —> b] 로가는 “최단거리” 보다 [a—>k—>b]로 가는 거리가 “ 더 짧은지” 검사한다. (그리고 더 짧으면 그 값으로 [a→b]값을 ]update)

7
1 2 4
1 4 6
2 1 3
2 3 7
3 1 5
3 4 4
4 3 2

• 테이블
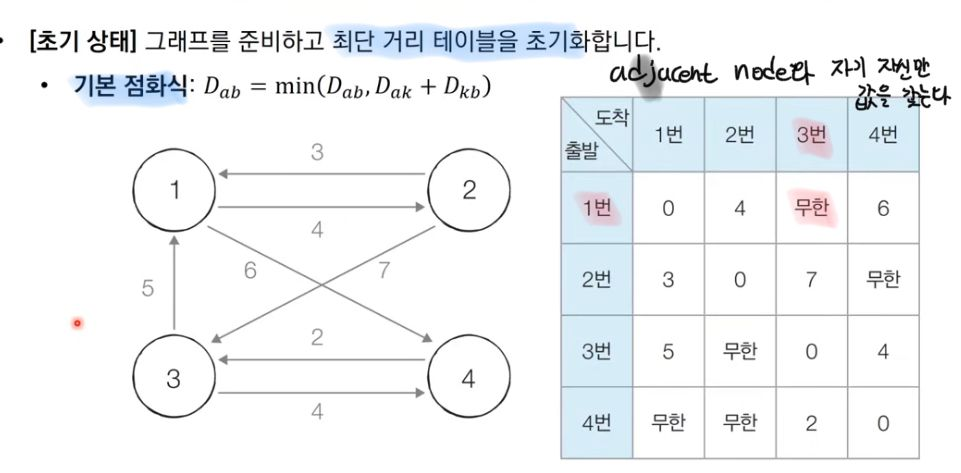
  • 맨 처음 초기화 : 인접노드에 대한 값만을 갖는다. / 나머지 노드 : 무한 의 값을 assign.
  • 이후, 각 노드에 대해 각각, 각 노드를 거쳐가는 경우를 확인하여 전체 테이블을 갱신.

과정

• 1번 노드를 거쳐 가는 경우 : k가 1인 경우.

• ex. 기존에 (2,4)는 무한 이었는데, [2–>1]이 3이고, [1–>4]가 6이라서, 1을 거친 (2,4)가 9로 갱신되었음을 볼 수 있다.

• 즉, k번째 노드를 거쳐 가는 경우에 갱신 되는 원소들의 조건은

  1. 테이블이[r][c]에서 r or c가 k가 아니고
  2. r ≠c 인 원소 들.

• 즉, k라는 변수 이용해, 모든 노드에 대해 하나씩 확인하며 해당 노드를 거쳐가는 경우를 고려할 수 있도록 하고, 그 때 마다 매번, 모든 a,b에대해 점화식을 갱신하기 때문에, 이를 구현 할 때는 삼중 반복문을 이용해서 전체 알고리즘을 구현 할 수 있다.

• 최종

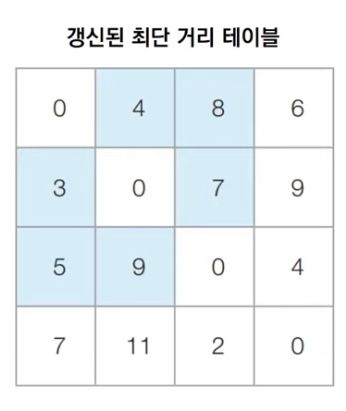
구현

• (I Think) 사실 아직 이제 DP라는 것은 잘 이해가 되지 않는다.

• 다익스트라 알고리즘과 달리, 최소경로 노드를 찾는 과정 없이, 순차적으로, 모든 노드를 k 로 하는 for문을수행한다. (가장 바깥 for 문은, 1번 노드부터 n 번 노드까지 값을 갖는 k 이다)

  • 이 안에서는 D(a,b) 를 업데이트 하기 위해 이중 for문을구현한다.
  • 이 때 이 2중 for 문은
    1. a or b 가 k가 아니어야 하고
    2. a ≠ b 인 경우에 대해서만 수행한다.

#include<iostream>
#define NUMBER 4
#define INFINITE 200000000 // 2억

int table[NUMBER][NUMBER]; //  1번 노드 = 0 번 노드  
int e; // 간선의 개수 

void floyd()
{
	for (int  k= 0; k < NUMBER; k++) {

		for (int a = 0; a < NUMBER; a++) {
			for (int b = 0; b < NUMBER; b++) {
				if (a != b & a != k & b != k) {
					//(a,k) +(k,b)
					int temp = table[a][k] + table[k][b];
					if (temp < table[a][b]) table[a][b] = temp; 
				}
			}
		}
	}
}
void printTable()
{
	for (int i = 0; i < NUMBER; i++)
		for (int j = 0; j < NUMBER; j++) {
			printf("%d --> %d :",i + 1, j + 1);
			if (table[i][j] == INFINITE) printf("No way to get there\n");
			else printf(" %d\n", table[i][j]);
		}
}
int main()
{
	std::cin >> e; 
	
	//초기화
	for (int i = 0; i < e; i++) {
		int v1, v2,w;
		std::cin >> v1 >> v2>>w; // start , end, weight
		
		table[v1 - 1][v2 - 1] = w; 
	
	}
	// i == i 가 아닌 노드  & 0 값을 갖는 노드 --> 무한 값을 갖도록 한다. 
	for (int i = 0; i < NUMBER; i++) {
		for (int j = 0; j < NUMBER; j++) {
			if (i != j & !table[i][j]) table[i][j] = INFINITE; // stdlib에 INFINITY가 defined되어있음. 	
		}
	}
	floyd();
	printTable();
}

동빈나 코드에서 python 문법 보기

파이썬에서 리스트 생성하며 초기화 하는 기법을 따로 정리

INF = int(1e9) # 무한을 의미하는 값으로 10억 설정
#사용자 입력받기
n = int(input()) # 사용자로부터 입력받은 것을 int형으로 변수에 대입
m = int(input()) # 사용자로부터 입력 받은 것을 int형으로 변수에 대입.
# 2차원 리스트를 만들며, 초기값을 부여
# 리스트는 이런식으로도 생성이 가능하지 [1]*5 을 하면 [1,1,1,1,1]
# 그런데 이것을 n+1 번 한다는 것은, 2차원 list를 만들겠다는 것. 
graph = [[INF]*(n-1) for _ in range(n+1)]

성능분석

• 노드의 개수가 N개일때 알고리즘 상으로 N번의 단계를 수행하는데
  • 각 단계마다 O(N^2)의 연산을 통해, 현재 노드를 거쳐 가는 모든 경로를 고려한다.
• 따라서, 플로이드 워셜 알고리즘의 총 시간 복잡도는 O(N^3)입니다.
• 따라서, 실제 플로이드 워셜이 사용되야 하는 경우 : 노드의 개수가 500개 이하로, 작은 개수인 경우!!
  • 500 500 500은 1억이 넘어가기 때문에.. 시간제한이 넉넉하지 않으면 이마저도 시간 초과 판정 받을 수가 있다.
  • 따라서 최단 거리 문제 출제시, 다익스트라, 플로이드 워셜 중 어느 것이 적절한지는 문제마다 고민하고, 그 고민 후, 적절한 알고리즘을 선택해야할것.