[백준] 12100번 2048(Easy)
문제 이해하기
한 번의 이동
- 전체 블록을 이동
- 네 방향 중 하나로 이동
-
(주의)한 칸만 이동하는게 아님. 예를들어 , 위로 이동을 하면 왼쪽그림 → 오른쪽 그림이 된다.

-
- 이 이동에서 이미 합쳐진 블록은, 또 다른 블록과 다시 합쳐질 수 없다.
- 그렇다면 어느 칸부터 이동시켜야할까?
-
주어진 조건에 의하면 , “이동하려고 하는 쪽의 칸이 먼저 합쳐진다”
-
예를들면 아래 “그림14”를 위로 이동시키는 경우.
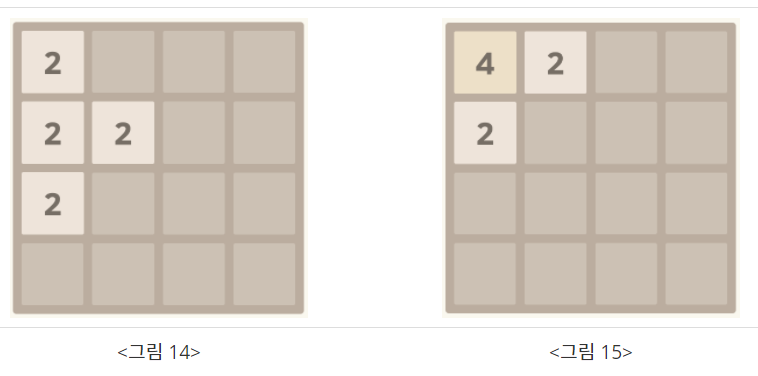
-
문제 해결하기
이미 합쳐진 칸인지 여부를 체크하기 위한 visit 배열을 생성한다.
- 이 배열은 각 이동( 큰 하나의 이동 ) 때 마다, 초기화 시켜줘야 한다.
이동을 어떻게 하는게 좋을까?
int[][] moves = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};board를 전체 탐색하면서
- 어떤 이동을 할 때 마다, visit을 초기화 해 두고 시작해야한다.
- → 인 경우는 가장 오른쪽에 있는 column 부터 시작해서 0이 아닌 칸을 만나면, 해당 칸을 이동시켜야 하기 때문에, 해당 칸을 이동시킬 다음칸 을 찾아야 한다.
- 각 이동별 함수를 작성한다. (이건 어쩔 수 없는 듯 )
public void left(){
// visit을 초기화
initVisit();
for(int r =0;r<n;r++){
for(int c = 0; c<n; c++){
if(board[r][c] == 0) continue;
findC(r,c,방향);
}
}
}
다음칸을 찾기
모든 방향에 대하여 적용 할 수 있는 메소드를 생각 해 보자
- 이 메소드에서, 기존 칸을 0으로 만들어주도록 해야한다.
- 합치는 경우를 제외하고는, 들어가서는 안되는 칸을 만날 때 까지 반복하게 되기 때문에, 현재 칸 이전 칸 또한 저장하고 있어야 한다.
- 그리고는 들어가선 안되는 칸을 만난 경우, “이전칸”에 값을 저장해야 한다.
- 즉, 다음 칸을 찾기 위해 변수 r,c를 사용한다고 칠 때, r,c는 "들어가서는 안 될 칸" 위치를 저장 할 수도 있게 된다. 그렇다면 그 이전의 r,c,값이 결국" find대상인 칸" 일 것이다. 따라서 이를 위해 변수 r,c 외에도 nr,nc라는 변수를 두어, 이전의 r,c값을 저장 해 두도록 한다.즉, 실제 "find대상인 칸"을 저장하고 있는 변수는 nr,nc가 된다.
public void findC(int preR,int preC, int dir){
int pre = boad[preR][preC];
// 기존 칸은 0으로 만들어줘야 한다.
board[preR][preC] = 0;
int cur = 0;
// moves[dir][0] moved[dir][1]
int r = preR + moves[dir][0];
int c = preC + moves[dir][1];
int nr = r, nc = c;
while(r<n && c<n){
// 언제까지 ?
// 1. 다음칸에 숫자가 있음
// 1-1. pre와 같지 않은 수 -> stop
// 1-2. pre와 같은 수 &&
if((cur=board[r][c]) != 0){
if( cur != pre) break;
// pre와 같은 수 && cur이 이미 합쳐진 수
if( visit[r][c] ) break;
// 합친다 -> 합친 경우 직접 합친 값을 세팅하고 return한다.
board[r][c] = cur<<1;
visit[r][c] = true;
nr = r; nc = c;
return;
}
// 2. 다음카에 숫자가 없는 경우 -> 이동한다
nr = r; nc = c;
r += moves[dir][0];
c += moves[dir][1];
}
// nr, nc가 구하고자 하는 다음 칸이다.
board[nr][nc] = pre;
return;
}가장 큰 값이 나올 수 있는 경우를 구해야한다
브루트 포스를 해도 되는가?
- 문제에서 최대 5번 이동이라는 제한을 뒀다.
- 이전 board를 복사 해 두어야 한다.
- 메모리가 얼마나 들까?
- 이동의 경우의 수는 4이기 때문에,
- 4^5 x 400 = 최소 40만 .. 여기에 정수 배 정도 더 들 수 있다.
- 따라서 재귀함수를 작성하는데, 해당 재귀함수에서는, left, right, up, down 모든 경우를 호출한다.
- 그 때 마다, 같은 board상태에서 각 경우를 시도해야하기 때문에, 매 번 이 재귀함수가 호출 될 때의 board 상태를 copy한다.
- 각 이동을 할 때마다, 그 상태의 board를 이용하여 다음 재귀함수를 호출한다.

package coding;
import java.io.*;
import java.util.*;
public class Main{
public static int n;
public static int[][] board;
public static int[][] copy;
public static boolean[][] visit;
public static int max = 0;
public static int[][] moves = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static StringTokenizer st;
public static void setting() throws IOException{
n = Integer.parseInt(br.readLine());
board = new int[n][n];
copy = new int[n][n];
visit = new boolean[n][n];
for(int r=0;r<n;r++){
st = new StringTokenizer(br.readLine());
for(int c=0;c<n;c++){
board[r][c] = Integer.parseInt(st.nextToken());
}
}
}
public static int findMax(int[][] b){
int cur = 0;
for(int r=0;r<n;r++){
for(int c=0;c<n;c++){
cur = Math.max(b[r][c],cur);
}
}
return cur;
}
public static void recur(int cnt,int[][] b){
if(cnt == 5){
// b에서 가장 큰 숫자
max = Math.max(findMax(b),max);
return;
}
// 매 번 b를 복사 해야함
int[][] cur = copy(b);
// left
left(cur);
recur(cnt+1,cur);
// right
cur = copy(b);
right(cur);
recur(cnt+1,cur);
// up
cur = copy(b);
up(cur);
recur(cnt+1,cur);
// down
cur = copy(b);
down(cur);
recur(cnt+1,cur);
}
public static int[][] copy(int[][] b){
int[][] cop = new int[n][n];
for(int r=0;r<n;r++){
for(int c =0;c<n;c++){
cop[r][c] = b[r][c];
}
}
return cop;
}
public static void left(int[][] b){
initVisit();
for(int r=0;r<n;r++){
for(int c=0;c<n;c++){
if(b[r][c] == 0)continue;
find(r,c,1,b);
}
}
}
public static void right(int[][] b){
initVisit();
for(int r=0;r<n;r++){
for(int c=n-1;c>=0;c--){
if(b[r][c] == 0)continue;
find(r,c,0,b);
}
}
}
public static void up(int[][] b){
initVisit();
for(int c=0;c<n;c++){
for(int r=0;r<n;r++){
if(b[r][c] == 0)continue;
find(r,c,3,b);
}
}
}
public static void down(int[][] b){
initVisit();
for(int c=0;c<n;c++){
for(int r=n-1;r>=0;r--){
if(b[r][c] == 0)continue;
find(r,c,2,b);
}
}
}
public static void find(int preR,int preC, int dir,int[][] b){
int pre = b[preR][preC];
// 기존 칸은 0으로 만들어줘야 한다.
b[preR][preC] = 0;
int cur = 0;
// moves[dir][0] moved[dir][1]
int r = preR + moves[dir][0];
int c = preC + moves[dir][1];
int nr = preR, nc = preC;
// 실제 board 상에서, 찾는 다음 칸은 nr,nc 이다 . r,c는 다음 탐색 칸이 "불가능한 칸"일수도 있기 때문에 탐색용으로 사용.
while(r<n && r>=0 && c>=0 && c<n){
// 언제까지 ?
// 1. 다음칸에 숫자가 있음
// 1-1. pre와 같지 않은 수 -> stop
// 1-2. pre와 같은 수 && visit[r][c] == false 이면 합친다.
if((cur=b[r][c]) != 0){
if( cur != pre) break;
// pre와 같은 수 && cur이 이미 합쳐진 수
if( visit[r][c] ) break;
// 합친다 -> 합친 경우 직접 합친 값을 세팅하고 return한다.
b[r][c] = cur<<1;
visit[r][c] = true;
nr = r; nc = c;
return;
}
// 2. 다음칸에 숫자가 없는 경우 -> nr,nc 를 업데이트 한다.
nr = r; nc = c;
r += moves[dir][0];
c += moves[dir][1];
}
// nr, nc가 구하고자 하는 다음 칸이다.
b[nr][nc] = pre;
return;
}
public static void initVisit() {
for (int r = 0; r < n; r++) {
Arrays.fill(visit[r],false);
}
}
public static void main(String[] args) throws IOException{
setting();
recur(0,board);
System.out.println(max);
}
}
- 블럭의 이동은 [ 상 하 좌우 네 방향 중 하나로 이동 ]
- 근데 전체가 이동한다는 거임
- [ 같은 값 ] 을 갖 는 두 블럭이 충돌 → 두 블럭은 하나로 합쳐진다.
