[백준] 14500번 테트로미노

14500번: 테트로미노

정사각형 4개를 이어 붙인 폴리오미노 → 테트로미노

• 문제에서 , 이러한 테트로미노에 어떤 종류가 있는지 알려준다.

• N x M 인 종이 위에 테트로미노 하나를 놓으려 한다.

• 종이의 각 칸에는 "정수"가 하나 쓰여 있다.

• 테트로미노 하나를 적절히 놓아, 테트로미노가 놓인 칸에 쓰여있는 수들의 합을 최대로 하는 프로그램을 작성하라.

• 테트로미노는 [ 회전, 대칭 ] 을 시켜도 된다.

풀이생각

(44분)

• 가장 먼저드는 생각은 문제에서 주어진 도형들을 , 대칭, 회전 시킨 경우에 대한 자료를 먼저 다 만들어두고
  • 5가지 테트로미노 이지만
  • 회전, 대칭의 경우를 만들면
  • 10개가 넘는 경우가 나올 것임
• 완전탐색을 하는 것이다.
  • 즉, 각각의 경우에 대해, 모든 칸에서 해당 도형을 움직이며 합을 구한다.
• 그런데 N(세로) x M(가로) 는 최대 500까지
  • 어떤 칸을, 도형의 시작칸이라고 가정하였을 때
  • 500 x 500 x (약 20가지 경우) x 4(네 칸) 의 복잡도가 나오기에
  • 완전탐색을 하더라도 괜찮을 것 같다.
• 즉 이 문제는 완전탐색으로 풀어야 하는 듯 하다.

자 이제 경우의 수를 만들어 보자

현재칸으로부터 이동할 칸에 대한, x,y값을 저장한 경우들을 cases라는 배열에 저장했다.

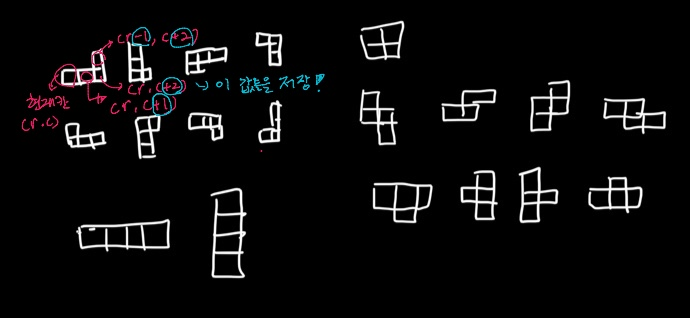
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    public static int[][][] cases
            = new int[][][]{ {{0,1},{0,2},{-1,2}},{{1,0},{2,0},{2,1}},{{1,0},{0,1},{0,2}},{{0,1},{1,1},{2,1}}
    ,{{1,0},{1,1},{1,2}},{{0,1},{1,0},{2,0}},{{0,1},{0,2},{1,2}},{{0,1},{-1,1},{-2,1}}
    ,{{0,1},{0,2},{0,3}},{{1,0},{2,0},{3,0}}
    ,{{0,1},{1,0},{1,1}}
    ,{{1,0},{1,1},{2,1}},{{0,1},{-1,1},{-1,2}},{{1,0},{0,1},{-1,1}},{{0,1},{1,1},{1,2}}
    ,{{0,1},{0,2},{1,1}},{{0,1},{-1,1},{1,1}},{{1,0},{-1,0},{0,1}}
    ,{{0,1},{0,2},{-1,1}}
    };
    public static int n,m;
    public static int max =0;
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static StringTokenizer st;
    public static int[][] arr = new int[500][500];
    public static void setting()throws IOException {
        st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());
        for(int i=0;i<n;i++) {
            st = new StringTokenizer(br.readLine());
            for(int j=0;j<m;j++) arr[i][j] = Integer.parseInt(st.nextToken());
        }
    }
    public static void solve(){
        int cnt=0;
        int x=0,y=0;
        boolean fail = false;
        for(int r=0;r<n;r++){
            for(int c=0;c<m;c++){
                //[r,c] 를 첫 시작점이라고 생각한다.
                // casese들을 돌아가며, 해당 테트로노미를 시작 칸을 [r,c]라고 한다.
                for(int tet=0;tet<cases.length;tet++){
                    cnt=0;
                    fail = false;
                    cnt+=arr[r][c];
                    // 테트로노미가 될 각 칸의 위치를 이용하여 각 칸의 값을 얻어온다
                    for(int dir=0;dir<cases[tet].length;dir++){
                        y = r +cases[tet][dir][0];
                        x = c +cases[tet][dir][1];
												// 테트로미노가 될 수 없는 경우라면 이 tet은 pass하기위해 boolean사용
                        if(y<0 || y>=n||x<0||x>=m) {
                            fail = true;
                            break;
                        }
                        cnt+=arr[y][x];
                    }
                    if(fail)continue;
                    // 모든 칸을 돌았다면
                    max = Math.max(max,cnt);
                }
            }
        }
    }
    public static void main(String[] args)throws IOException {
        setting();
        solve();
        System.out.println(max);

    }
}