-
이동 : 상하좌우로만 가능하다.
-
(0,0) —>(m-1,n-1)까지 이동 하려 한다.
-
높이가 더 낮은 지점으로만 이동하려고 한다.
-
이 때 이동할 수 있는 [경로의 개수 ] 를 구하기
-
문제 해결과정
- bfs를 사용하려고 한다.
- 이 문제는 "경로의 개수" 를 구해야 하기 때문에, visit여부를 따로 체크하지 않아도 되는 걸까??????
- 아 물론, 이 경로 상에서 이미 지나온 곳을 중복해서 방문하는 것은 안 되기 때문에... 아 그래서 bfs말고 dfs를 사용해야 할 수도 있겠다.
- visit을 사용한다.
- bactkrack 할 때는, 방문 여부를 해제한다.
- 각 depth의 노드가 모두 같은 경로는 없을 것이기 때문이다.
- 시간복잡도.....거의 완전탐색에 가까운 백트랙킹인데, 그러면 ... n,m이 500이하여도...이거 안될 것 같은데...
- 이 문제를 bfs로 푼다면 visit여부 따로 체크하지 않아도, 다시 되돌아 가지 않는다. 왜냐하면 " 더 낮은 지점으로만! " 이동 하기 때문임.
- 하지만, 메모리 초과가 생길 것이 예상된다.. visit을 따로 체크하지 않는 만큼 중복해서 25000^3만큼의 중복이 생길 수가 있다
틀렸다.--> 역시 DP로 풀어야 할 것 같다 : PriorityQueue를 이용한 DP로 풀었다
- 문제 해결과정 2
- "내리막길" 이기 때문에, 높은 곳에서 낮은곳으로의 이동만 가능하다.
- 즉 어떤 칸의 인접한 네 칸 중, 이 칸까지의 경로에 영향을 줄 수 있는 것은, 이 칸 보다 더 높은 높이를 가진 칸 뿐이다.
- 이 문제를 DP로 푸려고 생각하면 이런생각이 든다.
- 각 칸에는 그 칸까지의 경로의 개수를 저장한다.
- 특정 칸까지의 경로의개수는, 특정칸에 인접한 칸들까지의 경로를 모두 합한 것과 같다.
- 이 생각의 문제점은, 방문 순서다. 이를테면 (0,2)를 구하는데 (1,2)가 쓰인다. 하지만 이 때 (1,2)까지의 경로의 개수는 구해지지 않았을 수 있다. ( 내리막으로 이동이라서, (1,2)까지의 경로를 구하는데에는 (0,2)가 쓰이지 않는다)
- 따라서 들었던 생각은, 높은 높이를 가진 칸들부터 해당 칸 까지의 경로를 구하는 것이다. 이를 위하여 PriorityQUeue를 사용했다. 큐에는 (y,x,h) 정보를 저장한다.
- 문제예시의 (1,1)같은 경우, 이 칸에 상하좌우 인접한 칸 중에는 50보다 높은 것이 없어, 이 칸까지의 경로는 존재할 수가 없음을 보고 생각했다.
- 높은 칸 주위에 다 낮거나 같은 칸 밖에 없다면.. 그 칸은 도달할 수도 없는 것이기 때문이다.
- 인접한 칸들까지의 경로의 수를 해당 칸에 대한 경로의 수로서, 모두 더해주는것을 사용한 다이나믹 프로그래밍 기법이다.
- 캐시 초기화
- [0,0] 칸에는 1을 넣어줘야, 예를들어 위의 예제에서 (1,0) 에 대한 경로를 구할 때 cache[0,0]+cache[1,1] 이 0이 나오지 않는다.
- 복잡도
- 전체 탐색을 1회 시행한다. —> PQ에 넣기 위함 : O(nlogn) 근데 n이 25000인..
- PQ에서 꺼낸 칸, 즉, 모든 칸에 대해 인접한 4칸을 확인하고 캐시를 업데이트한다 n*4 —> O(n)
public class Main{
public static int m,n;
public static int[][] cache;
public static int[][] table;
public static Queue<int[]> q = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
// height를 기준으로 내림차순
return o2[2]-o1[2];
}
});
public static int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
public static int path =0;
public static void Setting() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
n = Integer.parseInt(st.nextToken());
table = new int[m][n];
cache = new int[m][n];
for(int row=0;row<m;row++){
st = new StringTokenizer(br.readLine());
for(int col=0;col<n;col++)
table[row][col] = Integer.parseInt(st.nextToken());
}
// 0,0 칸 캐시를 1로 해야, 인접한 칸까지의 경로에 수가 더해진다.
cache[0][0]=1;
// PQ를 세팅한다.
// 첫 번째 줄은, (0,0)칸만 제외하고 넣어준다.
for(int col=1;col<n;col++)
q.add(new int[]{0,col,table[0][col]});
for(int row=1;row<m;row++){
for(int col=0;col<n;col++){
q.add(new int[]{row,col,table[row][col]});
}
}
}
public static void dp(){
int curH=0;
while(q.isEmpty()==false){
int[] cur = q.poll();
int path=0;
for(int dir=0;dir<dirs.length;dir++){
int y = cur[0]+dirs[dir][0];
int x = cur[1]+dirs[dir][1];
// 벗어나면 fail
if(y<0||x<0||y>=m||x>=n)continue;
// 더 높은 칸이면 path개수를 더한다.
if(table[y][x]>cur[2]) path+=cache[y][x];
}
//System.out.println(cur[0]+","+cur[1] +" : "+path);
// cache를 업데이트
cache[cur[0]][cur[1]]=path;
}
}
public static void main(String[] args) throws IOException{
Setting();
dp();
System.out.println(cache[m-1][n-1]);
}
}다른 사람들의 풀이법을 보았다. : DFS + DP
-
이게 내 방법보다 효율이 더 좋았다.
-
단순한 DFS를 이용하여 재귀적으로 찾아나간다면 , dfs를 이용한 백트랙킹 방식으로, 매우 많은 경우의 수를 다루게 되어 시간초과가 날 수 밖에 없다.
-
하지만 여기에 DP를 얹는다면 시간을 줄일 수 있다.
-
여기서는 cache[y][x]는 해당 칸 이 포함되는 경로의 개수를 의미한다.
-
만약, 어떤 경로를 통해서 [m,n]에 도달하는 경우, 해당 경로에 속하는 모든 노드들은 모두 [m,n]까지 도달 할 수 있는 것들이 된다.
-
또한 dfs의 경우, 모든 경로가 서로 다 다른 경로가 된다는 것을 기억하고 있으면 된다. (path의 구성이 모두 다르다)
-
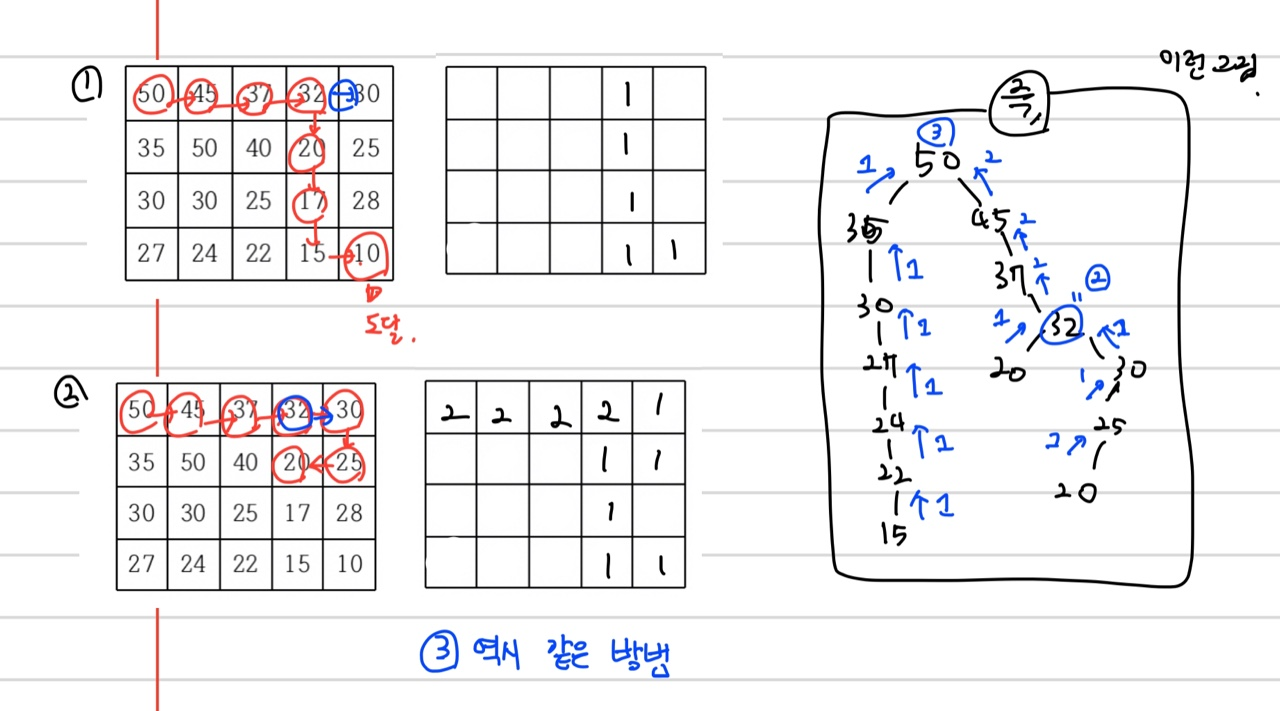
dfs를 이용한 backtrack의 경우, 각 경로가 넘겨주는 값을 통하여 , 현재 노드가 포함된 경로의 개수를 알 수가 있다. (그림을 보면 이해될 듯 하다 )
-
따라서, 이런그림으로 이해하면 된다.
- 1번으로 인해 20는 cache에 1을 가진 상태
- 2번 경로에서 20에 도달했을 때, cache가 1을 가졌음을 통하여 , 현재 경로로 [n,m] 도달이 가능함을 알 수 있다.
public class Main{
public static int m,n;
public static int[][] cache = new int[501][501];
public static int[][] table = new int[501][501];
public static int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
public static int path =0;
public static void Setting() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
n = Integer.parseInt(st.nextToken());
for(int row=0;row<m;row++){
st = new StringTokenizer(br.readLine());
for(int col=0;col<n;col++)
table[row][col] = Integer.parseInt(st.nextToken());
}
// cache를 -1로 세팅한다. dfs를 통해서 cache에 0이 들어올 것도 존재함을 생각하라.
// dp는 왠만하면 -1로 세팅하고 시작한다.
for(int row=0;row<m;row++){
Arrays.fill(cache[row],-1);
}
}
public static int dfs(int y,int x){
//System.out.println(y+","+x);
if(x==n-1 &&y==m-1) return 1;
if(cache[y][x]!=-1) return cache[y][x];
int path =0;
for(int dir =0;dir<dirs.length;dir++){
int ny=y+dirs[dir][0];
int nx=x+dirs[dir][1];
// 범위를 넘으면 pass
if(ny<0||nx<0||ny>=m||nx>=n) continue;
// 더 낮은 곳이 아니면 pass
if(table[ny][nx]>=table[y][x])continue;
int temp = dfs(ny,nx);
path+=temp;
}
cache[y][x]=path;
return cache[y][x];
}
public static void main(String[] args) throws IOException{
Setting();
dfs(0,0);
System.out.println(cache[0][0]);
}
}