[백준] 21923 곡예비행
- 상승비행 → 하강비행으로 변경 할 때에는, 다른 칸으로 이동 할 수 없다.
- 즉, 상승 비행이 끝난 칸에서, 하강비행을 시작해야 한다.
- 상승 비행 중에는, 앞or위로만 이동
- 하가 비행중에는 앞 or 아래로만 이동
이 대회에서 얻을 수 있는 최대 비행 점수?
- 입력 : N(세로) x M(가로)
문제 이해
- 상승 비행 → 하강비행 으로는 “ 한 번 만 “ 변화 한다.
- 상승비행 → 하강비행으로 변화한 경우, ( 변화하기로 한 칸의 점수를 한 번 더 더한다)
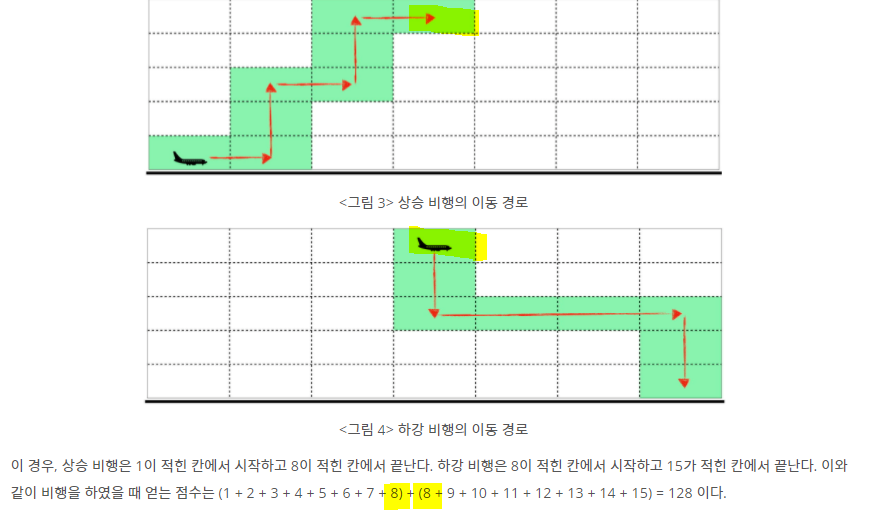
- 최대 경우 ? → 위로 1000번, 옆으로 1000개, 아래로 1000 개 인데 점수가 10000 → 최대 3000만.. ⇒ int 형으로 해도 된다고 생각했음.
- 그리고 이 문제는 n,m이 1000이니 절대 완전탐색은 아니고 , 동적계획법만이 생각났다.
문제 풀이
이 문제는 상승 → 하강을 무조건 해야한다.
또한, 상승 → 하강 시에는 칸을 이동하지 않는다 → 따라서 하강 직전 상승에서 방문한 칸은 하강에서 첫 방문하는 칸이 된다.
그리고, 상승하고 있을 때 가능한 이동과 하강하고 있을 때 까능한 이동이 다르고, 그에 따라 각 칸에서 가능한 최대값이 달라질 수 있다 생각하여 dp를 삼차원 테이블로 하여( dp[][][2] ) 로 하였다.
dp[][][0] 은 하강중일 때에 대한 것, dp[][][1] 은 상승 중일 때에 대한 것으로 해야한다고 생각했다.
만약 dp[i][j][upOrDown] 은 up 또는 down 상태인 [i][j]지점 ~ 끝점까지의 최대값 이라고 한다면
- dp[i][j][1] 은
- 현재칸에서 상승한 경우
- 현재칸에서 오른쪽으로 이동
- 현재칸에서 하강으로 변화
- dp[i][j][0]은
- 현재칸에서 오른쪽으로 이동
- 현재칸에서 아래로 이동
의 max 값에 + board[i][j] 한 값이된다.
따라서 현재 (i,j) 칸을 방문할 때의 상태를 추적해야한다.
이 경우 문제에서 원하는 값은 dp[n-1][0][1] 이다.
나는 이 방법을 사용했었고, 다른 분의 풀이 영상에서는 아래 방법으로 한 것을 보았다.
만약 dp[i][j][1] 은 “시작점” ~ dp[i][j][1] 까지의 최대값 이라고 한다면,
- dp[i][j][1] 은
- 상승상태 + 왼쪽에서 이동 : dp[i][j-1][1]
- 상승상태 + 아래쪽에서 이동 : dp[i+1][j][1]
- 둘 중 max 에 + 현재 칸의 점수 (board[i][j])
- dp[i][j][0]은
- 상승상태 + 이 자리 : dp[i][j][1]
- 하강상태 + 왼쪽에서 이동 : dp[i][j-1][0]
- 하강상태 + 위에서 이동 : dp[i+1][j][0]
에다가 (현재 칸의 값인 board[i][j] 를 더해줘야한다 )
여야 한다.
그리고 문제에서 원하는 것은 dp[n-1][m-1][0] 값이다.
시작점이 존재한다 ⇒ 시작점은 [n-1][0] 이고, 시작점은 무조건 상승으로 시작하기 때문에 dp[n-1][0][1] = board[n-1][0] 으로 세팅 하고 시작한다.
public static final int UP = 1;
public static final int DOWN = 0;
public static final int INIT_DP = -1000_0000_0;
public static final int INIT_LEN = 1000;
public static int n,m;
public static int[][] board = new int[INIT_LEN][INIT_LEN];
public static int[][][] dp = new int[1000][1000][2];
public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
public static StringTokenizer st;
public static void setting() throws IOException {
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
for(int i=0;i<n;i++){
st = new StringTokenizer(br.readLine());
for(int j=0;j<m;j++){
board[i][j] = Integer.parseInt(st.nextToken());
dp[i][j][0]=INIT_DP;
dp[i][j][1]=INIT_DP;
}
}
// 최대값 : 2000 x 10000 이니까..
// dp 의 초기화 : Integer.MAX_VALUE 해도 될 듯
}
// 출발 점 : n-1,0
// 도착 점 : n-1,m-1
public static int solve(){
dp[n-1][0][UP] = board[n-1][0];
// 우리가 목표하는 지점 : 하강으로 -> 종착점까지 온 경우이기 때문에
return dp2(n-1,m-1,DOWN);
}
/**
* 시작점 [n-1][0] 부터 , [j][j] 까지의 최대값을 구하기
* */
public static int dp2(int r, int c, int st ){
// range
if( r<0 || c<0 || r>n-1 || c > m-1) return INIT_DP; // 이거 그대로 해도되나??
if(dp[r][c][st] != INIT_DP) return dp[r][c][st];
int max = Integer.MIN_VALUE;
// 하강
if( st == 0){
// 상승칸 + 이자리 그대로 ( 상승 -> 하강 될 때는, 칸은 그대로인데 또 방문하기 때문)
max = Math.max(max, dp2(r,c,UP));
// 하강 상태 + 왼쪽에서 이동해옴
max = Math.max(max, dp2(r,c-1,DOWN));
// 하강 상태 + 위에서 이동해옴
max = Math.max(max, dp2(r-1,c,DOWN));
max += board[r][c]; // 현재 칸
}else{
// 상승상태 + 왼쪽에서 이동 해 옴
max = Math.max(max, dp2(r,c-1,UP));
// 상승상태 + 아래에서 이동 해 옴
max = Math.max(max, dp2(r+1,c,UP));
max += board[r][c];
}
return dp[r][c][st] = max;
}
public static int aSolve(){
dp[n-1][m-1][0] = board[n-1][m-1];
return dp1(n-1,0,1);
}
// 현재 칸을 방문할 때의 상태 -> up
// up 이 0 -> (상승상태), 1 -> (하강상태)
public static int dp1(int r, int c, int up){
if( r<0 || c<0 || r>n-1 || c > m-1) return INIT_DP; // 이거 그대로 해도되나??
if(dp[r][c][up] != INIT_DP) return dp[r][c][up];
int max = Integer.MIN_VALUE;
// up
if(up == 1){
// 상승
max = Math.max(max, dp1(r-1,c,up));
// 오른쪽
max = Math.max(max, dp1(r,c+1,up));
// 하강
max = Math.max(max, dp1(r,c,0));
}else{
// 오른쪽
max = Math.max(max, dp1(r,c+1,up));
// 하강
max = Math.max(max, dp1(r+1,c,up));
}
return dp[r][c][up] = max + board[r][c];
}
..... main 어쩌고
}