https://www.acmicpc.net/problem/1005

문제 이해하기

4번을 위해선, 2번 3번이 완료되어야 한다.

2번,3번은 “동시 진행이 가능" 하다 → 결국 나중에 완료되는 건물에 걸리는 시간이 측정된다

• 특정 건물만 짓는다면 게임에서 이길 수 있다.
• 매 게임마다, 특정 건물을 짓기 위한 순서가 달라진다.
• 특정건물을 가장 빨리 지을 때 까지 걸리는 최소시간?

4 3
5 5 5 5
1 2
1 3
2 3
4

1. 테스트 케이스
2. 건물개수 N, 규칙 개수 K
3. 각 건물 건설 비용 ( N 개 )
4. 건설 순서 규칙 ( K 개 )

풀이하기

위상정렬로 풀이 변경

• 방향성이 존재하고, Acyclic(싸이클이 존재하지 않음 ) 한 그래프 → DAG
  • 싸이클이 존재한다면, “순서"가 없는 거라 위상정렬로는 풀 수 없다.
• 이 경우, 목표 지점까지의 순서가 존재하게 되고 ( 물론 많은 경우들이 존재함 ) 이를 위상정렬을 사용하여 풀이할 수 있다.

위상정렬

• 그래프의 어떤 노드를 방문하기 위해서는, 반드시 선행 노드들이 이미 모두 방문되어야 하는 것.
• 하나의 조건이 만족되면
  • 이를 조건으로 하던 모든 노드 의 진입차수를 1씩 감소시킨다.
  • 그 결과 진입차수가 0이 된 노드 들을 “Priority Queue” 에 넣는다.
  • 그럼 현재의 큐 에는 “현재 건설 가능한 건물들" 이 들어가 있다. → 여기서 “가장 오랜 시간이 걸리는 애"의 시간만을 사용한다.

구현

틀린 생각

뒤집어서 풀어야겠다고 생각했던 이유는, “시작점"을 모르겠어서…라고 생각했는데

• 생각해보니 진입차수가 0인 점들이 시작점들 아닌가……
• 동일한 레벨에서 “진입차수가 0인" 것들을 모두 PQ 에 넣고 ( Max heap )
  • root 노드의 시간만 계산
  • 모든 노드들에 대해 하위 노드의 진입차수를 1씩 감소시킨다.

위에서부터 차례로 진입차수가 0인 노드들을 먼저 넣고 빼는 식으로 해도 되긴 할 듯 하다.

1. 규칙들을 방문하면서, 각 노드의 진입차수를 기록한다.
2. 규칙들을 방문하면서, 해당 노드가 “조건"인 노드들을 “해당 노드의 차일드 노드"로 등록한다
3. 진입 차수가 0이면서, 방문한적 없는 노드들을 Max heap 에 넣는다.
   1. 이 때, 해당 노드가 타겟 노드라면 바로 리턴하며, 이제까지의 시간 + 타겟 노드 시간을 더한다.
   2. 그렇지 않은 경우, max heap
4. 타겟 노드의 진입차수가 0이라면, 타겟 노드의 시간을 리턴하고 종료한다
5. 타겟 노드의 진입차수가 0이 아니라면

내가 생각했던 위 방법의 문제점

• 진입 차수가 0 인 애들 중 최대인 애만큼의 시간이 걸린다고 가정해버리면,
  • 사실 그 최대인 시간을 갖는 노드는, 선행노드가 아닌 경우가 존재한다. 그럼에도 그 시간을 선행 시간이라고 치게 되어서 아래와 같은 경우가 생겨버린다.
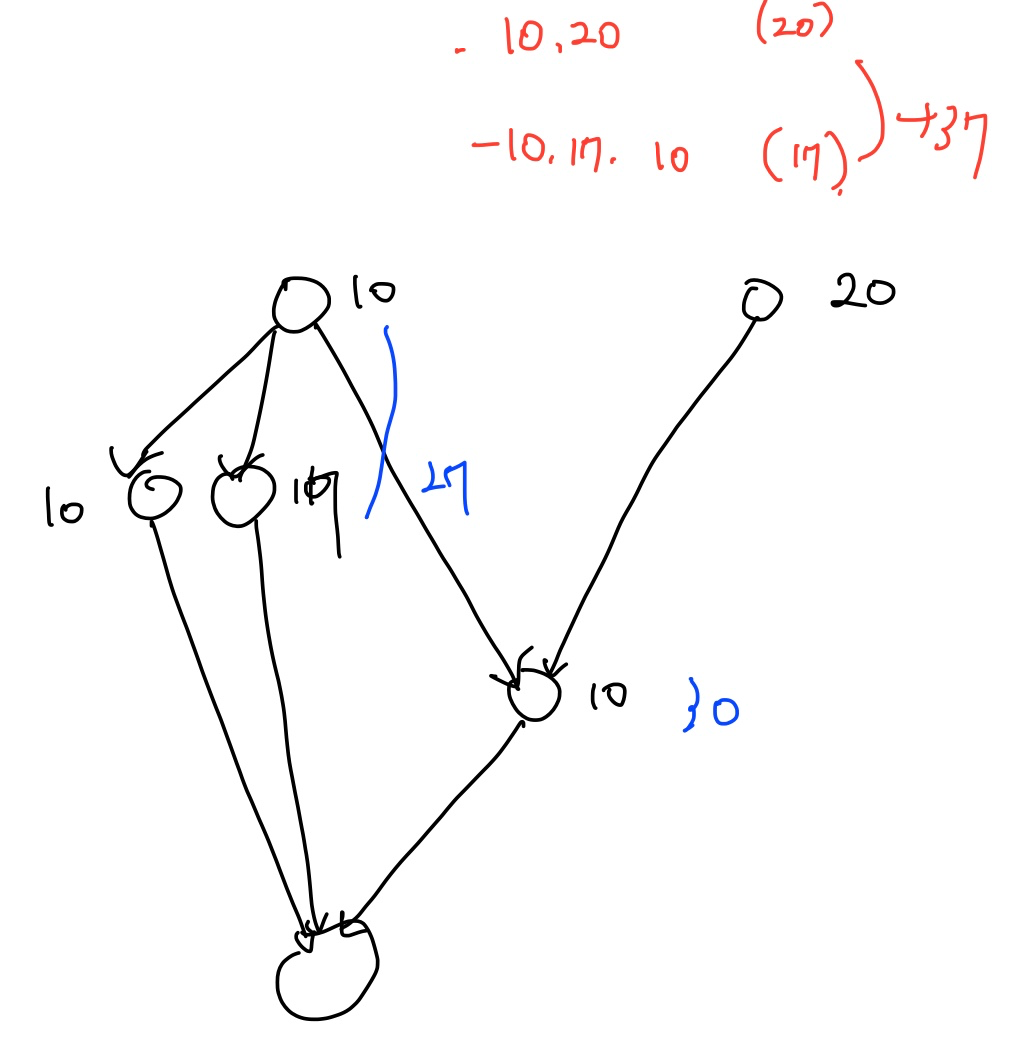
    • 아래의 경우, 최소시간은 30 + à 다. 그런데 내가 생각하던 방식대로 할 경우 37 + à 가 나오게 된다.

다른 풀이

• 선행 노드가 하나 이상 존재하는 노드의 최소 건설시간 : “ 선행 노드 들의 최소 건설 완료 시간들 중 최대값 "
  • 즉, 하나의 노드에 대한 건설 시간을 각각 구해보는 것이다!
• 진입차수가 0 이 된 노드에 대하여
  • 선행 노드의 최소 건설시간들의 최댓값 + 현재 노드의 건설시간을 계산하면 된다.

이렇게 문제를 풀기 위해서는 어떻게 해야할까?

• 각 노드의 child node 뿐만 아니라
  • 이렇게 하는 이유는, p 노드를 방문한 경우, p의 child 노드에 대한 진입차수를 1씩 감소해야하기 때문
• 각 노드의 parent node 들도 저장해야하는 것 같다
  • 이렇게 하는 이유는, child 노드에 대한 최소 건설시간을 구하기 위해서는, 바로위 parent 노드들에 대한 최소 건설시간의 최댓값 을 구해야하기 때문이다.

전체 노드는 1000 이하

만약, 각 노드의 부모가 1000개, 자식이 1000개 더라도, 2000 x 1000 → 200만정도?

풀리긴 할 것 같음.

1
4 4
10 1 100 10
1 2
1 3
2 4
3 4
4

1
8 8
10 20 1 5 8 7 1 43
1 2
1 3
2 4
2 5
3 6
5 7
6 7
7 8
7

package learningJava.algorithm;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.Optional;
import java.util.StringTokenizer;

public class Main {

    private BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    private int[] times; // 각 건물 짓는데 걸리는 시간
    private int[] minTime; // 각 건물 짓는데 걸리는 최소시간
    private int[] adjNumb; // 진입차수
    private boolean[] visit;
    private List<List<Integer>> childG = new LinkedList<>(new LinkedList<>());
    private List<List<Integer>> parentG = new LinkedList<>(new LinkedList<>());
    private StringTokenizer st;

    public void run() throws IOException {
        int t = Integer.parseInt(br.readLine());
        int n = 0, k = 0, w = 0;
        for (int i = 0; i < t; i++) {
            st = new StringTokenizer(br.readLine());
            n = Integer.parseInt(st.nextToken()); // 건물의 개수
            k = Integer.parseInt(st.nextToken()); // 규칙 개수

            // 초기화
            times = new int[n + 1];
            adjNumb = new int[n + 1];
            visit = new boolean[n + 1];
            minTime = new int[n + 1];
            childG.clear();
            parentG.clear();

            // 각 노드에 대한 List 를 추가
            for (int j = 0; j < n + 1; j++) {
                childG.add(new LinkedList<>());
                parentG.add(new LinkedList<>());
            }

            // 건설 시간
            st = new StringTokenizer(br.readLine());
            for (int j = 1; j < n + 1; j++) {
                times[j] = Integer.parseInt(st.nextToken());
            }
            // 건설 순서
            for (int o = 0; o < k; o++) {
                st = new StringTokenizer(br.readLine());

                int x = Integer.parseInt(st.nextToken()); // x 는 y 의 전제 조건 -> y 는 x 의 하위노드
                int y = Integer.parseInt(st.nextToken());

                childG.get(x).add(y);
                adjNumb[y]++;

                parentG.get(y).add(x);
            }
            // 목표 건물
            w = Integer.parseInt(br.readLine());

            System.out.println(solve(w));
        }
    }

    public int solve(int target) {
        Optional<Integer> next;

        while ((next = nextNode()).isPresent()) {
            int cur = next.get();

            // 선행 노드들에 대한 시간들 중 max
            int maxParent = parentG.get(cur).stream()
                .map(node -> minTime[node])
                .max(Comparator.comparing(x -> x))
                .orElse(0);

            minTime[cur] = times[cur] + maxParent;

            // 진입 차수 감소시키기
            for (Integer child : childG.get(cur)) {
                // 자식 노드의 진입차수를 1 감소시킨다
                adjNumb[child]--;
            }

        }

        return minTime[target];
    }

    // 진입 차수가 0 인 노드 찾기 - 없으면 empty optional
    private Optional<Integer> nextNode() {

        for (int idx = 1; idx < adjNumb.length; idx++) {
			if (visit[idx] || adjNumb[idx] != 0) {
				continue;
			}
            visit[idx] = true;

            return Optional.of(idx);
        }

        return Optional.ofNullable(null);
    }

    public static void main(String[] args) throws IOException {
        Main main = new Main();

        main.run();
    }
}

찝찝한 코드 - Optional..

Optional 을 parameter 에 사용하지 않는 게 좋은 이유는 아래와 같은 글들을 본적이 있다.

그리고 isPresent(), get() 을 사용하는 것 역시 좋지 않은 예시라고 들었다.

그런데 isPresent(), get() 을 사용하는 중이라 매우 찝찝하다..

Java static code analysis: "Optional" should not be used for parameters

자바 언어에서 Optional 은 리턴타입으로 사용되는 것을 목적으로 만들어졌다. 해당 메소드가 값이 아닌 것(null) 을 반환할 수도 있음을 나타내는 용도가 주된 용도라고 볼 수 있다.

Optional 을 parameter 로 사용하게 되면, 기존에는

• nul
• non null

이 두가지 경우의 parameter 가 오는 것만을 예상하고 이에 대한 처리를 해 주면 되었었는데,

이제는 세 가지 경우가 나오게 되는 것임

• null
• non null without value
• non null with value