백준_1753번 [다익스트라 최단경로]

• 동빈나 코테 준비 에서 내가 배운 알고리즘 상, 최단 경로 알고리즘으로는 "디익스트라 알고리즘" 이 있다.

• 사실 동빈나 영상을 보고, 직접 디익스트라 알고리즘을 구현해 본 후, 이틀 후 복습 차원에서 풀어본 문제이긴 하다.

• priority_queue 를 사용함에 있어, (vertex, 최단거리) 인 pair<int,int> 객체들이 "최단거리" 기준으로 PQ에 insert되도록 하기 위해, 세 번째 인자에 대한 customcompare를 선언했다. - 그런데 다른사람들의 코드를 보니 여기에 그냥 greater<pair<int,int>> 를 사용해도 괜찮더라.

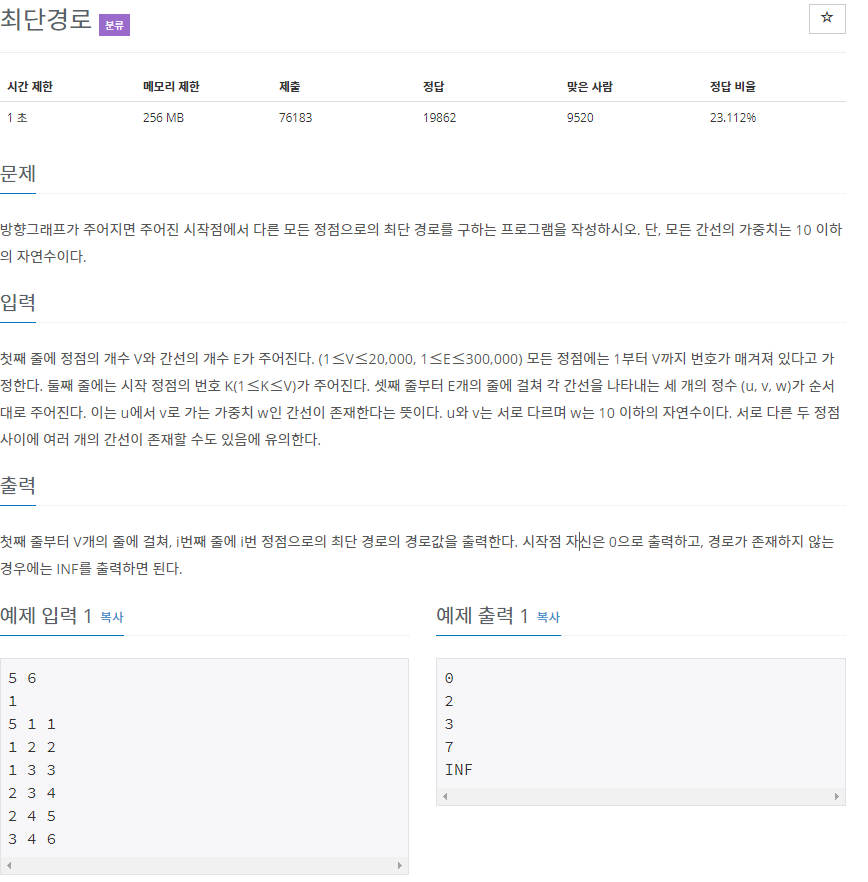
• 현재 vertex의 개수는 1<=v<=20,000 이기 때문에 개선된 디익스트라 알고리즘을 사용해야 한다. (반복하는 상황 속에서 방문하지 않은 노드중 최단 거리를 갖는 노드를 선택하는 로직에서, 순차탐색을 하지않고, 우선순위 큐를 사용하는 방법)

• 유의 할 것 : 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수 있다.
  - 어차피 Directed Graph이기 때문에 Priority queue로 구현 시 그리 유의할 사항은 아닌 듯하다
  - 왜냐하면 : PQ에서 front()<pop()>으로 꺼낸 element는 d_table에 있는 거리 값과 비교하는 과정을 거친 후 ignore을 하는 등으로 여러개의 간선 중 결국 최단 거리가 되는 간선을 선택하게 되기 때문이다.

• C++로 작성했음에도 실행시간이 만족스럽지 않다.
  

#include <iostream>
#include <queue>
#include <vector>
#include <time.h>


using namespace std;
typedef pair<int, int> Node; // (vertex번호, weight)  

struct customCompare {
	bool operator()(Node& n1, Node&n2)
	{
		return n1.second > n2.second;
	}
};

int nv, ne,start;
int infinity = 200000000;

vector<Node> graph[20001];
int d_table[20001];
//priority_queue<Node, vector<Node>, greater<Node>> q;
priority_queue<Node, vector<Node>, customCompare> q;



void dikstra()
{
	int i;
	d_table[start] = 0;
	q.push(Node(start, 0));
	
	while (q.empty() == false)
	{
		Node cur = q.top();
		int cur_d;
		q.pop();
		//이미 처리한 노드는 ignore
		if (d_table[cur.first] < cur.second) continue;

		//인접노드확인 
		for (i = 0; i < graph[cur.first].size();i++)
		{
			Node adj = graph[cur.first][i];
			cur_d = cur.second + adj.second;
			//update + push to queue as Node(adj.first, cur_d)
			if (cur_d < d_table[adj.first])
			{
				d_table[adj.first] = cur_d;
				q.push(Node(adj.first,cur_d)); 
			}
		}
	}



}
int main()
{
	cin >> nv >> ne >> start;

	for (int i = 0; i < ne; i++)
	{
		int v1, v2, w;
		cin >> v1 >> v2 >> w; 
		graph[v1].push_back({ v2,w }); 
	}

	for (int i = 0; i <= nv; i++)
		d_table[i] = infinity;
	
	dikstra();

	for (int i = 1; i <= nv; i++)
	{
		if (d_table[i] == infinity)printf("INF\n");
		else printf("%d\n", d_table[i]);
	}

}