위상정렬

“순서가 정해져 있는 작업” 을 “ 차례로 수행 “해야할 때 , 그 순서를 결정해주기 위해 사용하는 알고리즘.

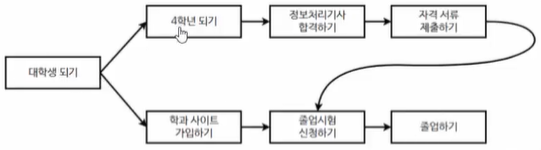
• 그래프의 “흐름”은 “조건”으로 해석할 수 있다.
  • 다양한 조건들이 얽혀 있을 때,즉 순차적으로 어떤 그래프가 형성되어있을 때, 모든 조건이 만족하는 경로를 일직선으로 나타낼 수가 있다
  • 위상정렬 : 대학생 되기 → 학과 사이트 가입 → 4학년 되기 → 정처기 합격하기 → 자격 서류 제출 → 졸업시험 신청하기 → 졸업하기
• 여러 개의 답이 존재할 수 있다.
• 그렇기 때문에 DAG ( Directed Acyclic Graph) 에만 적용 가능하다.

  • “조건” 은 “방향성” 이기도 하다.

  • cycle이 존재하는 경우, 위상정렬을 수행할 수 없다 :
    - 서로가 서로의 조건이 되는 것이기 때문임. ( 이뤄질 수가 없는거 )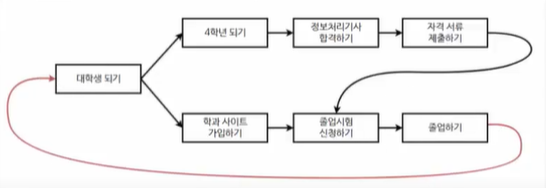

    

    이와 같은 그래프에선 위상정렬을 수행할 수 없다.

    위상 정렬은 시작점이 존재해야하는데, 위와 같은 사이클 그래프에서는 시작점을 찾을 수 없다.

1. 특정 그래프로 위상정렬을 할 수 있는지 없는지
2. 가능하다면 그 결과는 무엇인지

풀이 알고리즘은 두 가지 방식이 있다

• Stack 이용
• Queue를 이용

큐를 사용하여 위상정렬 수행하기

• 진입차수 : 특정 노드가 있을 때, 그 노드로 들어오는 다른 노드의 개수 , 위상정렬에서는 그 노드에 대한 “조건”의 개수

1. 진입차수가 0인 정점을 큐에 삽입한다.
   1. 진입차수가 0인 정점 : 조건이 모두 만족된 노드
2. 큐에서 원소를 꺼내, 연결된 모든 간선을 제거한다.
   1. 즉, “ 해당 원소를 조건으로 갖는 노드 “들의 진입 차수를 1씩 감소시킨다.
3. 간선 제거 이후, 진입차수가 0이 된 정점을 큐에 삽입한다.
4. 큐가 빌 때 까지 2~3번 과정을 반복한다. 모든 원소를 방문하기 전에 큐가 빈다면 cycle이 존재하는 것( 왜냐하면, a노드의 모든 조건 노드들이 충족되지 않아 큐에삽입 되지 않은 것이기 때문에 ) 이고, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상정렬의 결과다.

시간복잡도

O(v+e) 가 된다.

• 큐에는 V 개의 노드가 들어가고
• 각 노드에 대해 간선으로 연결되어있는 노들의 진입 차수에 대한 연산을 하기 때문에, 결과적으로 모든 간선 E 만큼 에 대한 연산이 들어감

따라서 O(V+E) 가 된다.

참조 : 유튜브_동빈나

27강 - 위상 정렬(Topology Sort) [ 실전 알고리즘 강좌(Algorithm Programming Tutorial) #27 ]