[프로그래머스]등굣길

코딩테스트 연습 - 등굣길

물에 잠기지 않은 지역을 통해 학교를 가려고 한다.

시작점(집) : (1,1)

학교 : (m,n)

이동: 오른쪽, 아래쪽으로만 이동

최단 경로 개수를 1,000,000,007 으로 나눈 나머지를 return

문제이해하기

아니 💥💥 격자..격자가 너무 헷갈리게 주어져있다;;

m x n 격자 모양이라더니, 학교의 위치는(4,3)이라더니...

보통 m x n 주어질 때 m이 row이 n이 col인데 여기선 💥💥반대로 주어져있다는 것에 매우매우매우 주의해야한다

와 그래서 puddles 도 거꾸로 해서 주는 것에 주의해줘야함

문제풀이

이 문제 역시 subproblem으로 나눠볼 수 있다. 즉 동적계획법 문제다.
현재는 (1,1) →(m,n)을 구하고 있지만, 그 사이에 있는 [a,b ]는 여러 경로에서 거치게 되는 길일 수 있다.

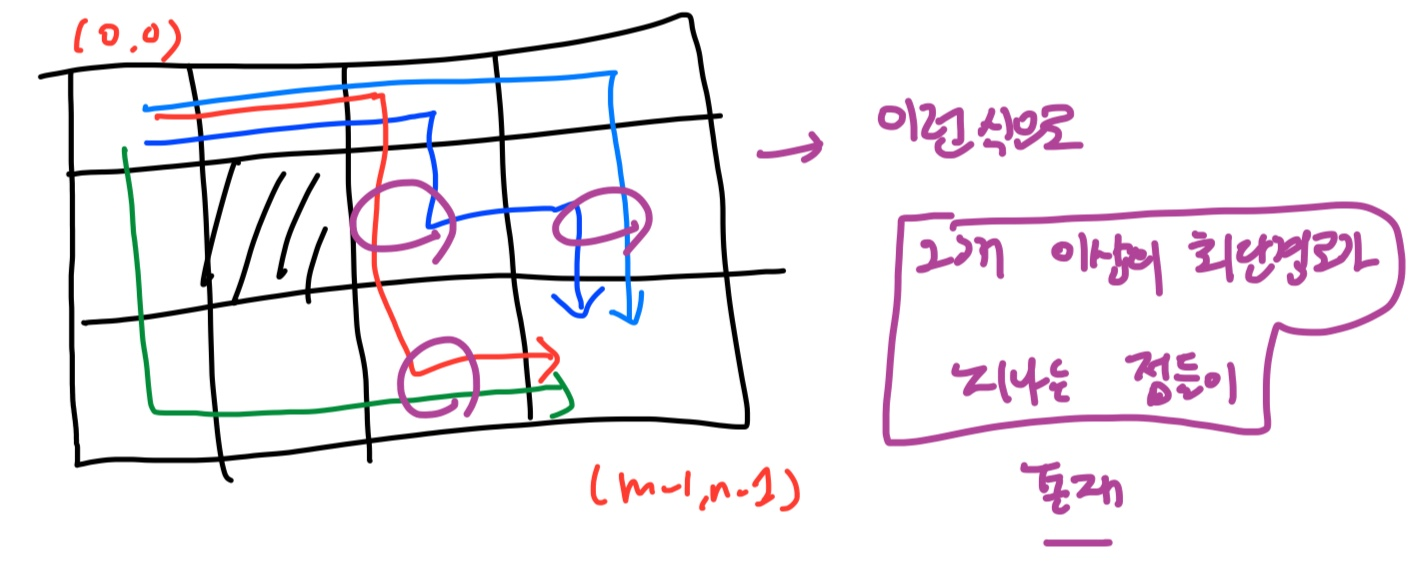
따라서 dp[r][c]를 두고, 이는 [r,c]로부터 [m-1,n-1]까지 가는데 최단경로의 개수 를 저장한다.

public int recur(int r, int c){
	if( r>m-1 || c>n-1) return 0; // out of range
	if( dp[r][c] == -2 ) return 0; // 물웅덩이 - board를 따로 두지 말자.
	if( dp[r][c] != -1 ) return dp[r][c]; // 이미 풀어진 subproblem
	if( r == m -1 && c == n-1) return 1; 
	return dp[r][c] = recur(r+1,c) + recur(r,c+1);

이 문제는 이동이 “오른쪽”, “아래쪽” 만을 가능하게 하기 때문에 문제가 매우 쉬워짐 -> 왜냐하면 ,“이동이 가능하기만해도 그 경로는 최단경로이기 때문임.

• 무슨 말이냐면,왼쪽, 위로도 이동이가능했다면, 결국 삥 둘러서 가는 경우도 나오는 경우가 있는데, 여기서는 그런 경우는 고려하지 않아도 되었기 때문임.

그리고 1,000,000,007로 나눈 나머지를 리턴하라고 되어있는데 이 덕분에 int range 범위의 값이 계속나올 수가 있음.

물론 이를 위해서는 각각의 재귀함수에서 리턴되어오는 중간결과값도 modulo를 시키고, 이들을 더하고 나서도 modulo를 시켜줘야함

import java.util.*;
class Solution {
    public int[][] dp = new int[100][100];
    public int gm,gn;
    public int DIVIDER = 1_000_000_007;
    public int solution(int m, int n, int[][] puddles) {
        int answer = 0;
        
        gm = m; gn = n;
        // dp 세팅
        for(int r=0;r<n;r++){
            Arrays.fill(dp[r],-1);
        }
        for(int[] p : puddles){
            // p[0]은 r, p[1]은 c
            dp[p[1]-1][p[0]-1] = -2; 
        }
        // solve
        answer = recur(0,0);
        // print();
        
        return answer;
    }
    public void print(){
        for(int r =0;r<gn;r++){
            for(int c = 0 ; c<gm;c++){
                System.out.print(dp[r][c]+" ");
            }
            System.out.println();
        }
    }
    public int recur(int r, int c){
        if( r > gn-1 || c > gm-1)return 0; // out of range
        if(dp[r][c] == -2 )return 0; // 물웅덩이
        if(dp[r][c] != -1) return dp[r][c]; // solved problem 
        if(r == gn-1 && c == gm-1) return 1;
        return dp[r][c] = (recur(r+1,c) % DIVIDER + recur(r,c+1) % DIVIDER ) % DIVIDER;
        
    }
}