[프로그래머스_카카오] 괄호 변환

(2:10)....... 푼 것에 의의를...

문제를 읽으며 드는 생각..

• 괄호의 짝 맞추기
• 균형잡힌 괄호 문자열 —> '('와 ')'의 개수가 같은 경우
  • 여기서 짝까지 모두 맞으면 → "올바른 괄호 문자열"
• 균형잡힌 괄호 문자열 —> 올바른 괄호 문자열로 변환하는 과정

1. 입력이 empty string —> 빈 문자열""을 반환
2. 문자열 w를 2개의 "균형잡힌 문자열" u,v로 분리 (???????이 분리를 어떻게 )
   • 이 때, u는 "더 이상 분리 할 수 없는" 균형잡힌 괄호 문자열"이다.
     • ??? 그게 무슨 말인데...........
   • v는 빈 문자열이 될 수 있다.
     • ??? 그렇구나...........
3. 문자열 u 가 "올바른 괄호 문자열"이라면 문자열 v에 대해 1단계부터 다시 수행합니다.
   1. 그렇구나..u를 참 잘 분리했었나보구나....
4. 문자열 u가 올바른 괄호 문자열이 아니라면 아래 과정을 수행한다.
   1. 빈 문자열을 둔다.
   2. 빈 문자열에 '('을 붙인다.
   3. 문자열 v에 대해 1단계부터 재귀적으로 수행한 결과 문자열을 이어붙인다
      • ????????..................................
   4. ')' 를 뒤에 붙입니다.
   5. u의 첫 번재와 마지막 문자를 제거하고. 나머지 문자열의 괄호 방향을 뒤집어 뒤에 붙인다.
   6. 생성된 문자열을 반환한다.

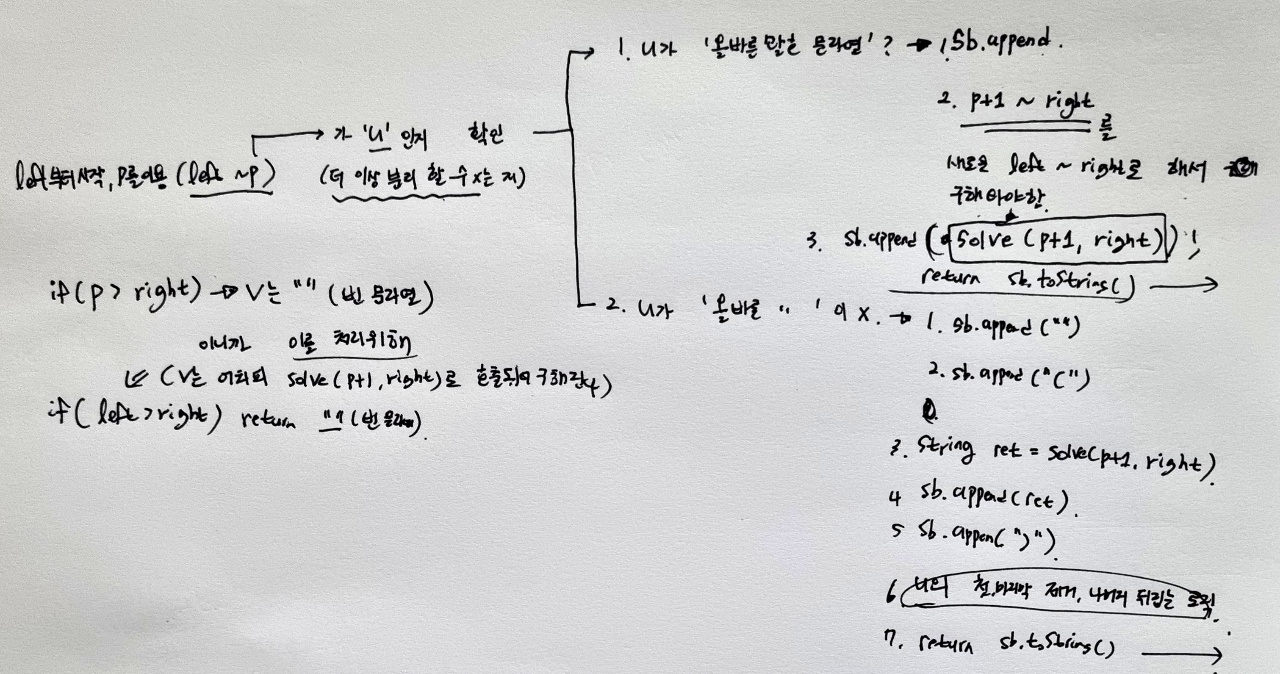
위와같은 혼란의 시간을 거쳐 일종의 pointer 역할을 하는 p라는 변수를가지고 target이라는 String에 대한 로직을 종이에 작성했다

문제 해설

"더이상 분리 할 수 없는 균형잡힌 문자열" u를 다루기 때문에, 중복된 경우가 나오지는 않을 것 같다. 아니다 v정도?

• 카카오가 코테 시간으로 무려 5시간이나 내놓는 이유를 알 것 같은 문제다

• 💥 일단 확실히 생각 해 놓 고 갈것 : u와 v는 이런식 :

  • [u][v] 또는 [v][u]다.

• ✋ 균형 잡힌 문자열 검증 로직 → 따로 필요없다. 어차피 ,u (더이상 분리할 수 없는 균형잡힌 문자열만 찾으면 된다 )

• ✋ "더이상 분리 할 수 없는 " 균형잡힌 문자열

  Stack stack
  char cur 
  ====
  시작 때 stack은 비어있을 수 있으니 일단 넣고봐야지 
  또한, 현재의 character가 stack에 있는 것과 같은 종류라면 넣는다.
  if(stack.top() == cur || stack.isEmpty()==true) { stack.push(cur)}
  현재의 character가 stack과 반대되는 거면, 짝을 이룬거니 stack 에서 pop만 해주면 된다. 
  else stack.pop();
  ====
  현재 글자에 대해 위의 로직을 하고 나서, 
  stack이 비어있다는 것은, 그 글자까지가
  더 이상 분리 할 수 없는 균형잡힌 문자열이라는 것을 의미
  stack.isEmpty() == null 되자마자 
  더이상 분리 할 수 없는 균형잡힌 문자열임을 의미한다. 

  • 가장왼쪽에서 or 가장 오른쪽에서부터 찾아야 하는가? → NO, 그냥 왼쪽에서만 찾아도 된다

    (()) --> O
    ()(()) -> X
    (()()) -->O
    )((()) ->X 

• ✋ 짝이 맞는다 ( 올바른 괄호 문자열의 조건 ) → 별도 검증

  • 우리가 흔히 아는 Stack을 사용해 보자 .

  • 검증 로직

    '('을 만나면 stack에 push
    ')'을 만나면 stack에 '(' 이 있어야 한다. 
    없는 순간 💥 "짝이 맞는게 아니다" 

• ❓ 문자열을 2개의 "균형잡힌 문자열" u,v로 분리하기 ???

  • 완전탐색을 해야하나 싶다. 어차피 [u][v]이니까.

• 이것도 일종의 완전탐색으로 풀어야만 한다고 판단된다.

• left~right 사이에 있는 p 라는 일종의 포인터역할을 하는 변수를 이용하여, u와 v를 분리한다고 생각하였다. p를 움직이며 u를 찾고 나면, 일정한 로직만을 구현해주면 된다.

  • 따라서 p는 left부터 시작하여 움직인다. right이하까지만 가능하다 ( 문자열 전체가 u 일 수 있기 때문에 right까지 p의 이동범위가 될 수 있다 )
    • 이 경우 v는 빈 문자열이어야 한다. 즉, 여기서도 재귀함수를 호출할 것인데, 호출되는 함수 측에서 left는 p+1이어야 한다 (당연하다 현재 left ~ p (boundary를 포함) 가 u에 해당 하기 때문 → p+1~ 끝 이 v에 해당하는데 , 현재 p+1이 이미 , 현재 문자열의 경계를 넘었기에 빈문자열이 리턴되어와야 한다. )

• if (p > right) 까지 p가 increment했다는 것은 v가 "" 즉 빈 문자열임을 의미한다. 이는 로직 내에서 , v 부분의 Sring을 구하기 위해 recur을 재귀 호출 할 때 , left로 p가 전달되고, right로는 기존의 right를 전달하여 재귀호출된 recur함수 쪽에서 left> right 로서 검출된다.
  

import java.util.*;
class Solution {
    public String target;
    public String solution(String p) {
        target = p;
        int left =0, right = target.length()-1;
        String answer = recur(left,right);
        
        return answer;
    }
    public String recur(int left, int right){
        if(left>right) return "";
        int p=left;
        StringBuilder sb = new StringBuilder("");
        while(p<=right){
            // left ~ p 가 u 인지(더이상 분리할 수 없는 균형잡힌 문자열) 확인
            if(atomicCheck(left,p)){
                // 올바른 괄호 문자열인지 확인
                if(pairedCheck(left,p)){
                    sb.append(target.substring(left,p+1));
                    sb.append(recur(p+1,right));
                    return sb.toString();
                }else{
                    //
                    //StringBuilder cursb = new StringBuilder("");
                    sb.append("(");
                    String add = recur(p+1,right);
                    sb.append(add);
                    sb.append(")");
                    makeStr(sb,left,p);
                    return sb.toString();
                }
            }
            else{
                p++;
            }
        }
        return "";
    }
    // u의 첫 마지막을 제거하고 나머지는 뒤집기( 그냥 바로, 호출측에서 사용하던 sb에 append) 
    public void makeStr(StringBuilder sb,int left, int right){
        int first = left+1;
        int last = right-1;
        for(int i=first;i<=last;i++){
            if(target.charAt(i)==')') sb.append("(");
            if(target.charAt(i)=='(') sb.append(")");
        }
    }

    // 더이상 분리 할 수 없는 균형잡힌 문자열인지 확인
    public boolean atomicCheck(int left, int right){
        Deque<Character> stack = new LinkedList<>();
        while(left<=right){
            if(stack.isEmpty()==true||stack.getLast()==target.charAt(left)){
                stack.add(target.charAt(left));
            }else{
                stack.removeLast();
            }
            if(stack.isEmpty())return true;
            left++;
        }
        return false;
    }
    // 올바른 괄호 문자열인지 확인
    public boolean pairedCheck(int left, int right){
        Deque<Character> stack = new LinkedList<>();
        while(left<=right){
            if(target.charAt(left)==')'){
                // stack에는 '('만 넣는다.
                if(stack.isEmpty()) return false;
                stack.removeLast();
            }
            else stack.add('(');
            left++;
        }
        return true;
    }
    
}

테스트 1 〉	통과 (0.18ms, 68.8MB)
테스트 2 〉	통과 (0.20ms, 70.5MB)
테스트 3 〉	통과 (0.27ms, 68.9MB)
테스트 4 〉	통과 (0.20ms, 60.1MB)
테스트 5 〉	통과 (0.24ms, 68.5MB)
테스트 6 〉	통과 (0.22ms, 74.2MB)
테스트 7 〉	통과 (0.33ms, 70.4MB)
테스트 8 〉	통과 (0.36ms, 72.7MB)
테스트 9 〉	통과 (0.24ms, 70.1MB)
테스트 10 〉	통과 (0.35ms, 69.9MB)
테스트 11 〉	통과 (0.49ms, 71MB)
테스트 12 〉	통과 (1.15ms, 70.4MB)
테스트 13 〉	통과 (1.51ms, 67.7MB)
테스트 14 〉	통과 (1.07ms, 60.9MB)
테스트 15 〉	통과 (1.10ms, 67.5MB)
테스트 16 〉	통과 (2.21ms, 59.8MB)
테스트 17 〉	통과 (6.86ms, 74.9MB)
테스트 18 〉	통과 (9.09ms, 76.2MB)
테스트 19 〉	통과 (5.18ms, 60MB)
테스트 20 〉	통과 (5.55ms, 60.6MB)
테스트 21 〉	통과 (13.81ms, 73MB)
테스트 22 〉	통과 (4.95ms, 72.5MB)
테스트 23 〉	통과 (3.11ms, 74.5MB)
테스트 24 〉	통과 (8.11ms, 72.3MB)
테스트 25 〉	통과 (8.46ms, 62.7MB)