1. Introduction
저자는 neural network가 over-parameterize 하지만 good-generalization의 결과에 주목하며 kernel-method와의 비슷함을 말한다.
그 이유에 대해 추측해보면, kernel method는 low-dimension input을 high-dimension으로-심지어는 infinite dimension까지-mapping해 선형 알고리즘을 사용한다. 그러므로 overfit할 위험이 있지만 regularization을 사용하면 generalization이 좋다와 비슷한 맥락이 아닐까?
Understand Deep Learning We Need to Understand Kernel Learning 논문에서도
"strong performance of overfitted classifiers is not a unique feature of deep learning" 라 말하며 실험적으로 kernel method도 비슷한 결과를 보였다고 한다.
또한 위에서 말한 regularization과 별개로 kernel method에 있는 'inductive-bias'가 good-generalization의 또 다른 요인이라고 말한다.
representation-theorem에 의해 finite한 training-data에 따라
kernel-method를 표현할 수 있기 때문인것 같다.
그리고 2020년에 나온 논문 "Every Model Learned by Gradient Descent Is Approximately a Kernel Machine" 에 따르면 gradient-descent롤 학습된 neural network도 kernel machine 처럼 trainig-data들의 similarity를 계산하는 kernel algorithm 임을 수학적으로 증명했다.
논문에서는 NTK를 정의하고 몇가지 property들(positive-definite)로 neural network의 특징을 설명한다. 수학적인 증명이 많아 이해할 수 있는 범위안으로 정리했다.
2. from linear regression to NTK
논문에서는 NTK를 kernel-gradient로 유도했는데 이해할 수 없어서 다른 자료들을 참고했다.
큰 틀은 neural-network의 layer를 무한으로 했을 때, weight-update가 거의 이뤄지지 않는다. 따라서 neural-network를 테일러급수를 통해 linearize 할 수 있다. 이 때 식의 꼴이 kernel-regression의 꼴과 유사함에 착안해 NTK를 유도하는 것이다.

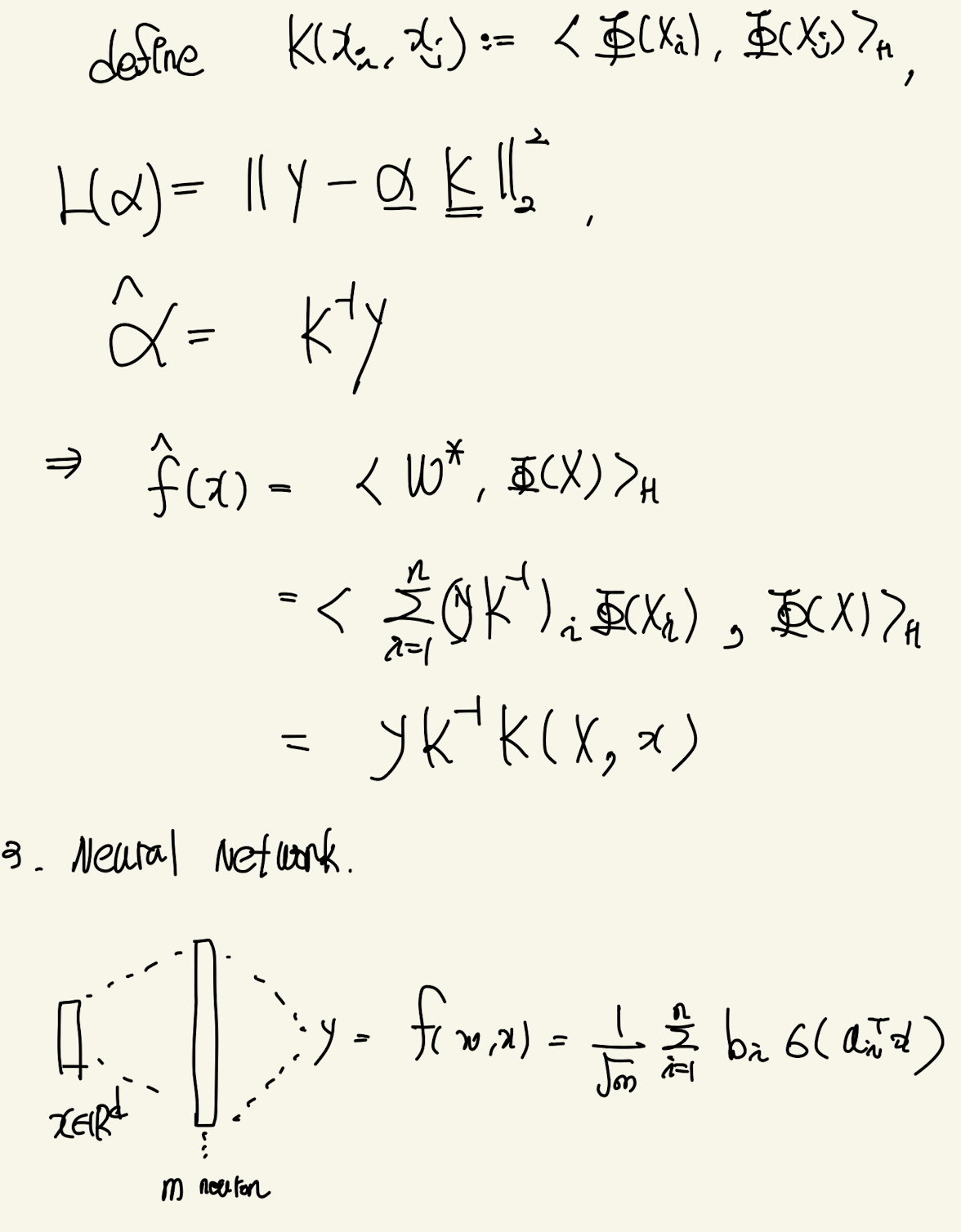
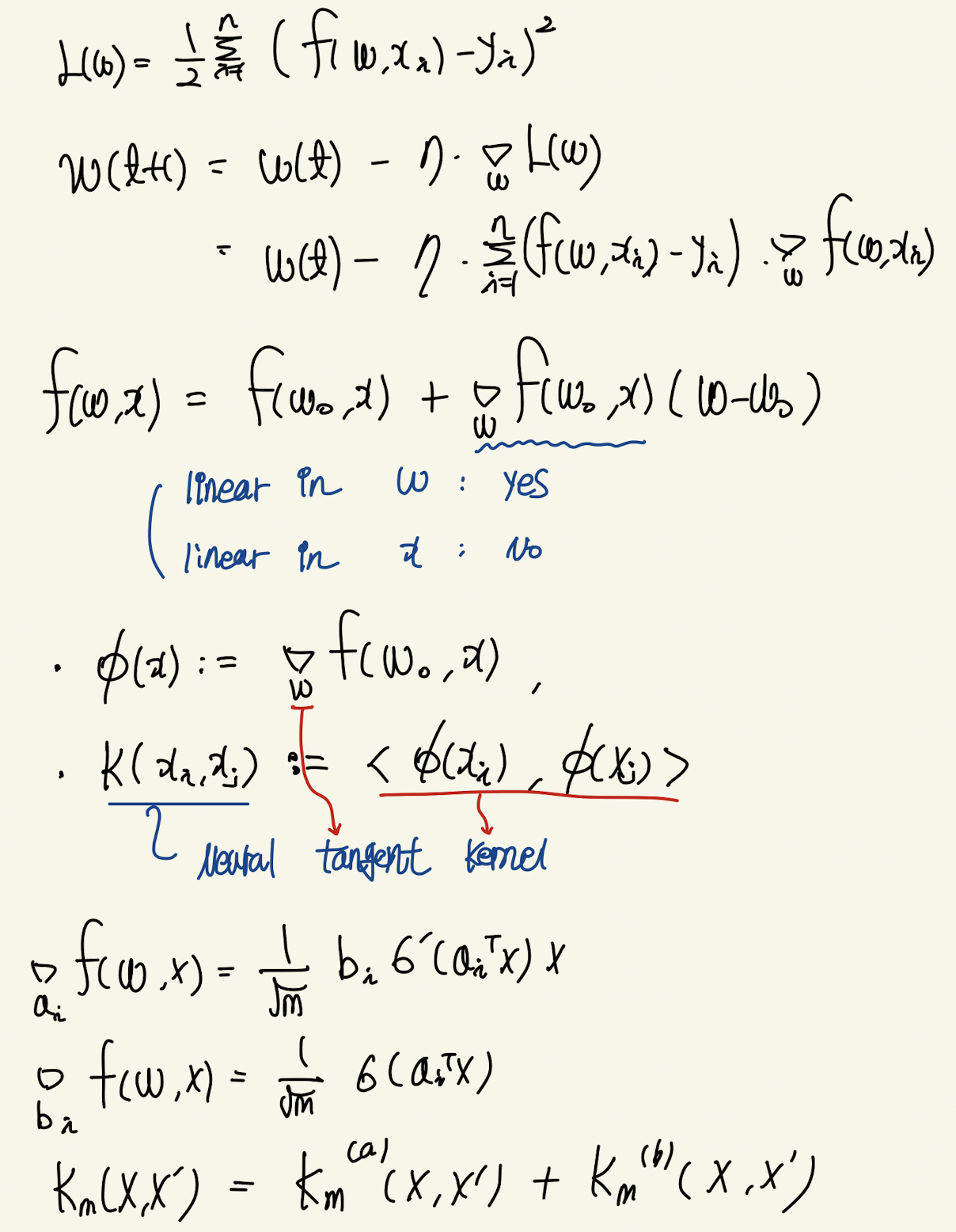
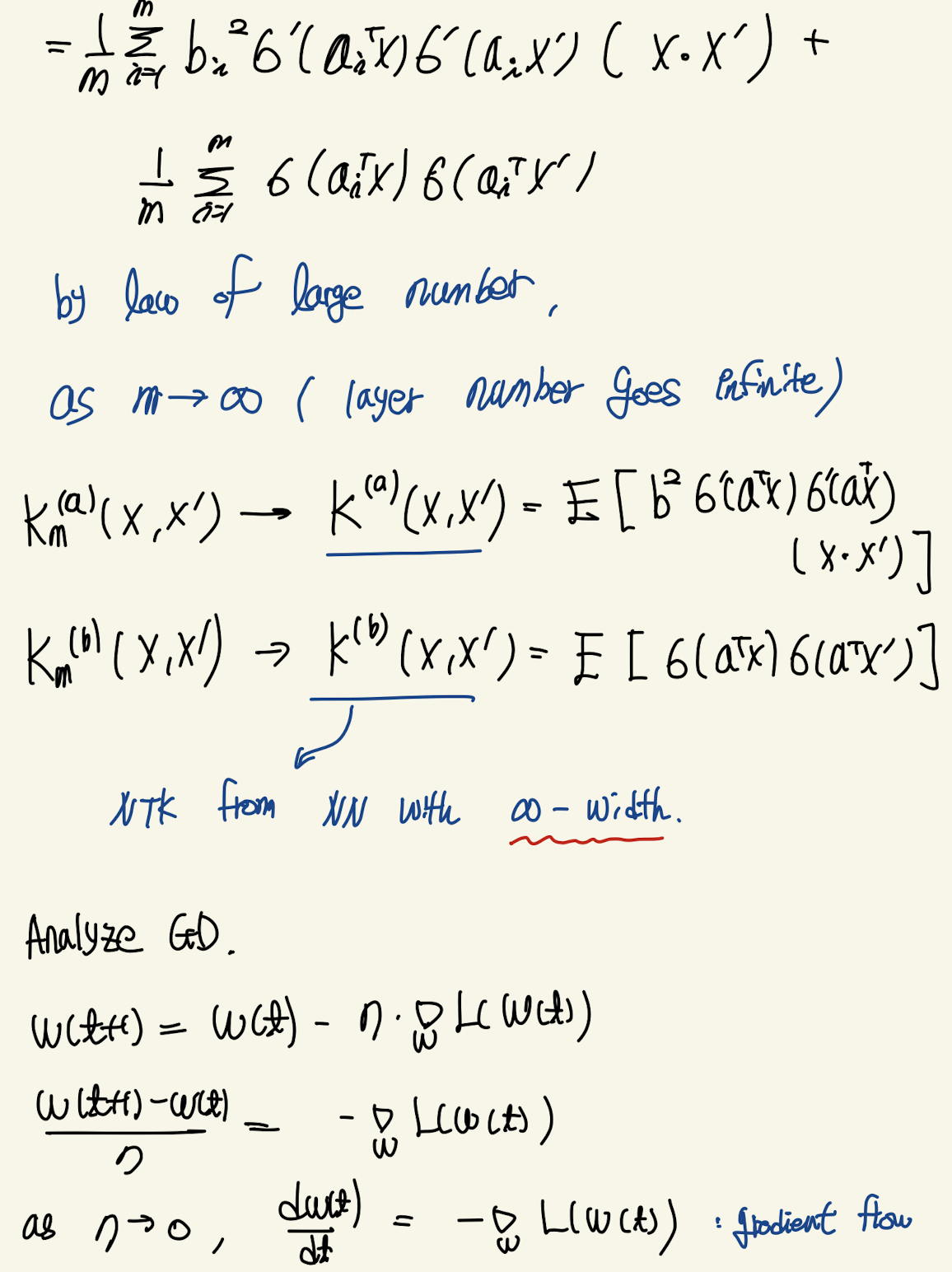


neural-network에 대한 가정은 m개의 neuron을 갖는 one-layer NN이다. layer의 크기가 클 수록 weight가 update되는 변화량이 작다는 것이 알려져있다. 즉 gradient update에 static하다는 것이다. 따라서 테일러 근사가 가능한 것이다. 이때 output에 대한 weight의 gradient가 input의 mapping function으로 봤을 때 NTK를 gradient의 내적으로 정의할 수 있다. 한가지 놀라운점은 처음에 neuron의 갯수를 m이라 가정하고 NTK를 계산할 경우 law of large number를 적용할 수 있게 된다. 따라서 infinite dimension을 갖는 neural-network의 NTK로 근사할 수 있다. 이를 이용해 gradient descent를 분석하면 neural network의 convergence 성질을 알 수 있다. least-square loss가정 하에서 dynamic of output을 chain-rule로 분해하면 NTK로 구성된 ode를 구할 수 있다. over-parameter regime에서 kernel은 positive-definite임으로 eigenvalue decomposition을 할 수 있다. 이 때 eigenvalue가 neural-network의 convergence rate이다.
이러한 분석을 통해 fourier feature가 NN으로 하여금 high-frequency 정보를 더 잘 학습하게 도와준다는 것을 알 수 있다. 일반적으로 natural-data들은 low-frequency 정보들의 magnitude가 크고 high-frequency 정보들의 magnitude는 작다. 이때 fourier feature를 통과한 input들의 NTK를 분석해보면 기존의 MLP NTK보다 eigenvalue falloff 가 크지 않음을 보였다. 이는 NN이 high-frequency까지 충분히 학습할 수 있음을 말한다.
