Reference
- 내용전반: edwith
🌀 Normalization (정규화)
🔸 정규화의 의미
정규화란, 하나의 relation에 하나의 의미만 존재할 수 있도록 relation을 분해해 가는 과정입니다. 이 과정에서 데이터의 중복이 있을 경우 이상 현상이 발생할 가능성이 있는데, 이런 불필요한 중복을 피하기 위해 스키마를 분해해서 정규화를 하게 됩니다
이렇게 정규화를 하면 자료를 저장하는 공간을 최소화할 수 있고 DB 내 데이터가 불일치되는 위험을 최소화하므로 좋은 DB 스키마를 설계하게 됩니다. 또한, 새로운 데이터가 삽입될 때 relation을 재구성할 필요를 줄일 수 있습니다. 그리고 보다 간단한 관계 연산에 기반해서 검색을 보다 효율적으로 할 수 있도록 해줍니다
정규화는 물리적인 설계의 마지막 단계에서 혹은 DB 설계를 마친 후에 설계 결과물을 검증하기 위해서도 사용됩니다
🔸 잘못 설계된 스키마 예시
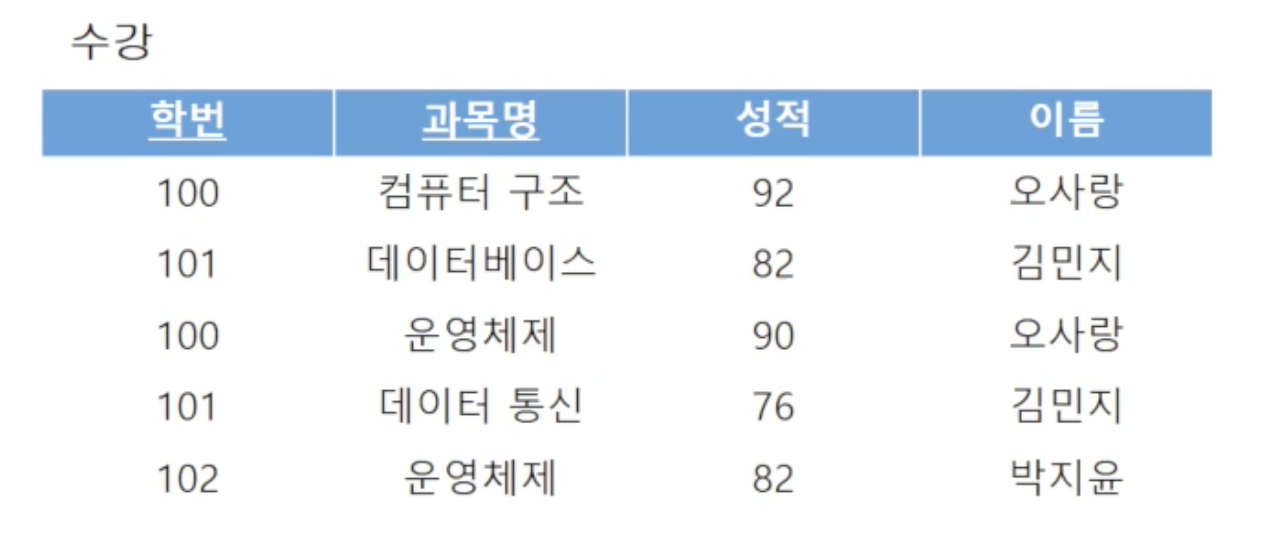
위는 DB 스키마가 잘못 설계된 경우를 보여줍니다. 왜냐하면, 이 relation은 학번과 과목명을 기본키로 가지는데, 학번이 100인 학생인 오사랑과 101인 김민지라는 이름이 중복으로 저장되기 때문입니다. 이는 중복 데이터로 인한 저장 공간 낭비뿐만 아니라 relation 갱신/삽입/삭제 시 이상 현상을 유발하게 됩니다
🔸 이상 현상
이상 현상이란, relation 설계가 잘못되어 발생한 불필요한 데이터 중복으로 인해 relation 갱신/삽입/삭제 시 문제가 발생하는 것
- 갱신 이상 (Update Anormaly)
- 삽입 이상 (Insertion Anormaly)
- 삭제 이상 (Deletion Anormaly)
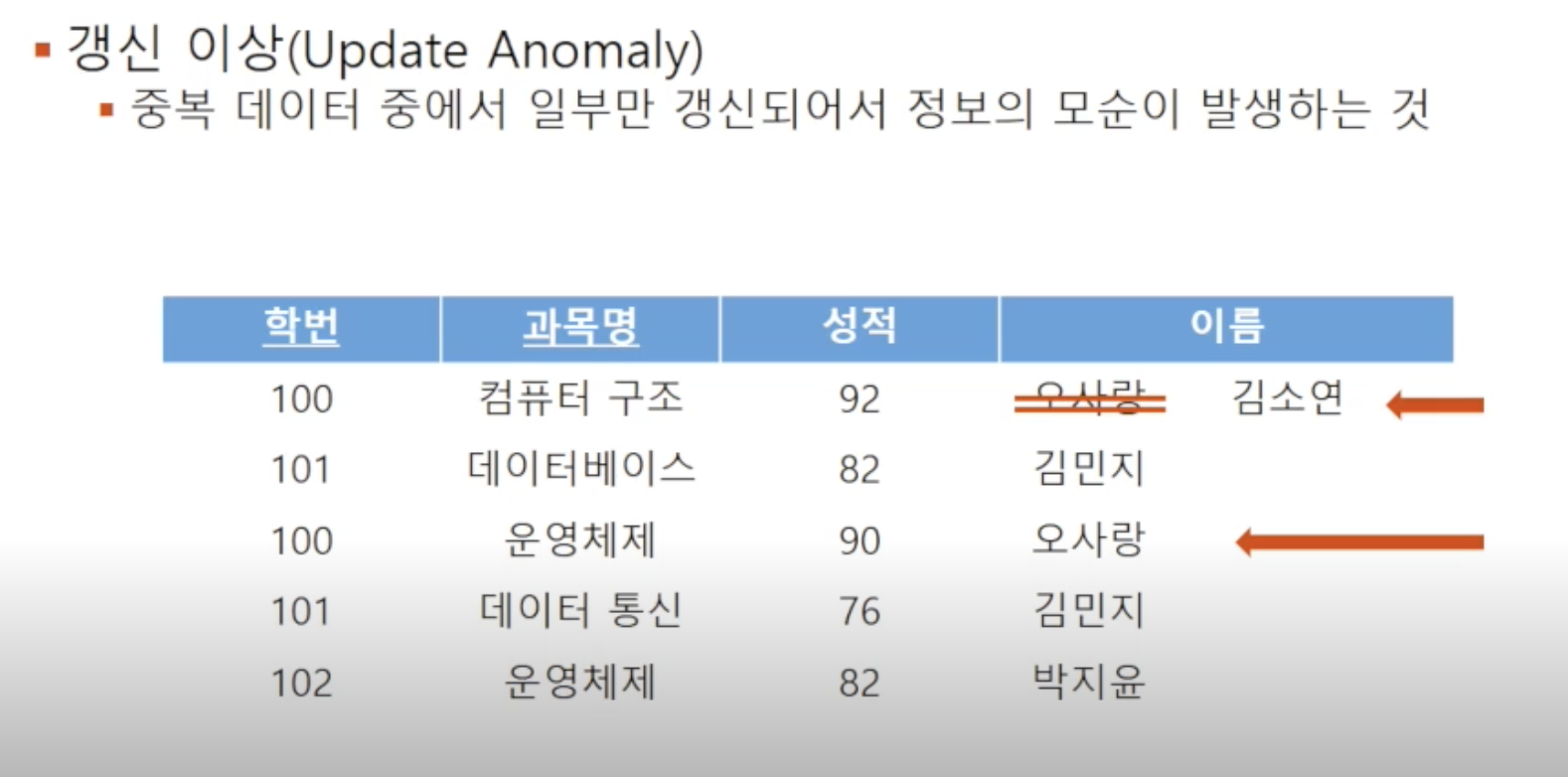
🔘 갱신 이상
중복되는 튜플 중 일부만 변경되어 데이터 불일치가 발생하는 것을 의미합니다
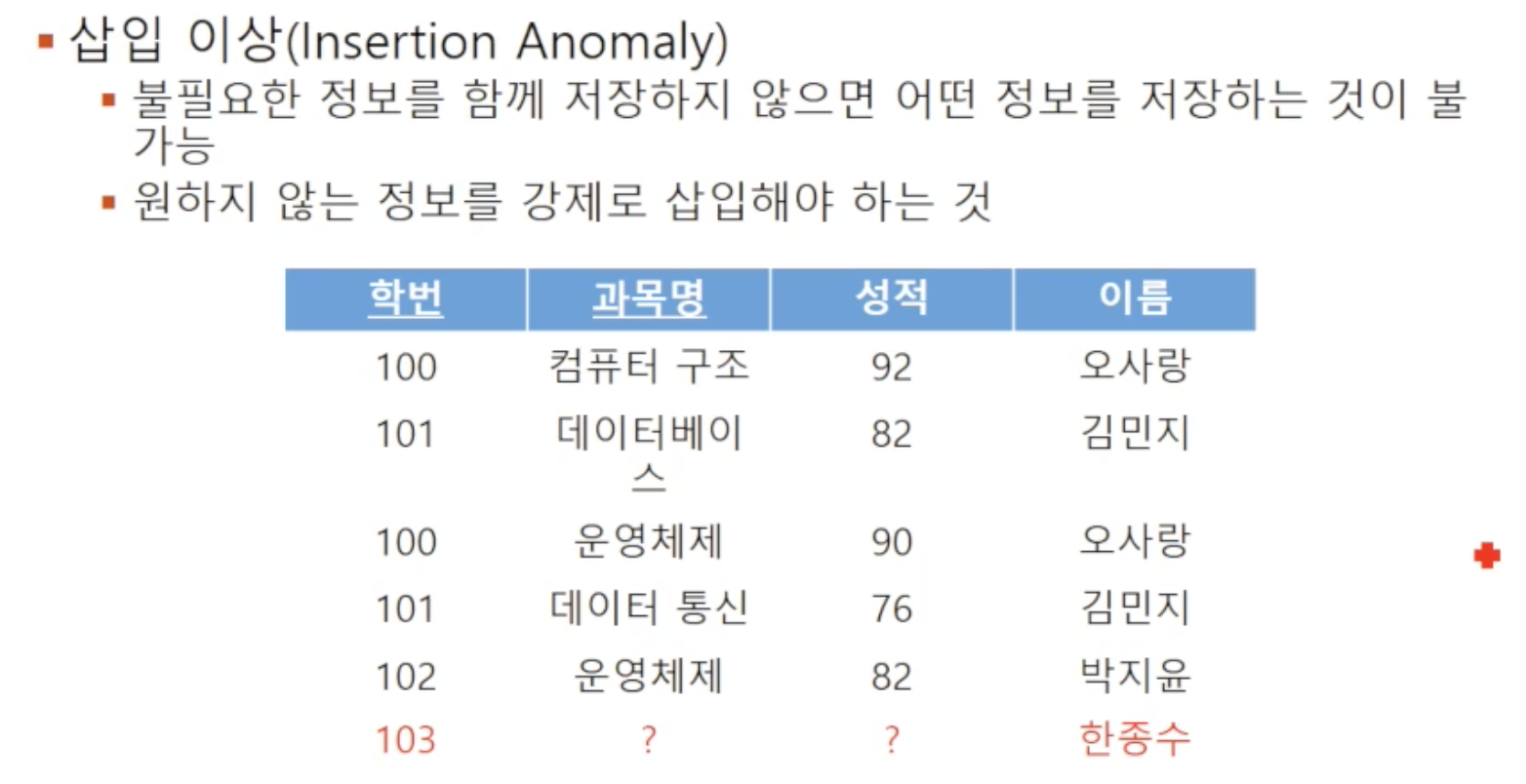
🔘 삽입 이상
불필요한 정보를 함께 저장하지 않으면 어떤 정보를 저장하는게 불가능한 것을 의미합니다. 위 예시에선 학번이 103번인 한종수 학생을 추가해야 하는 상황인데, 아직 수강신청을 하지 않아 기본키 구성요소인 과목명이 없어 relation에 추가할 수 없습니다. 꼭 필요하다면 가상의 과목명을 임시로 삽입해야 합니다
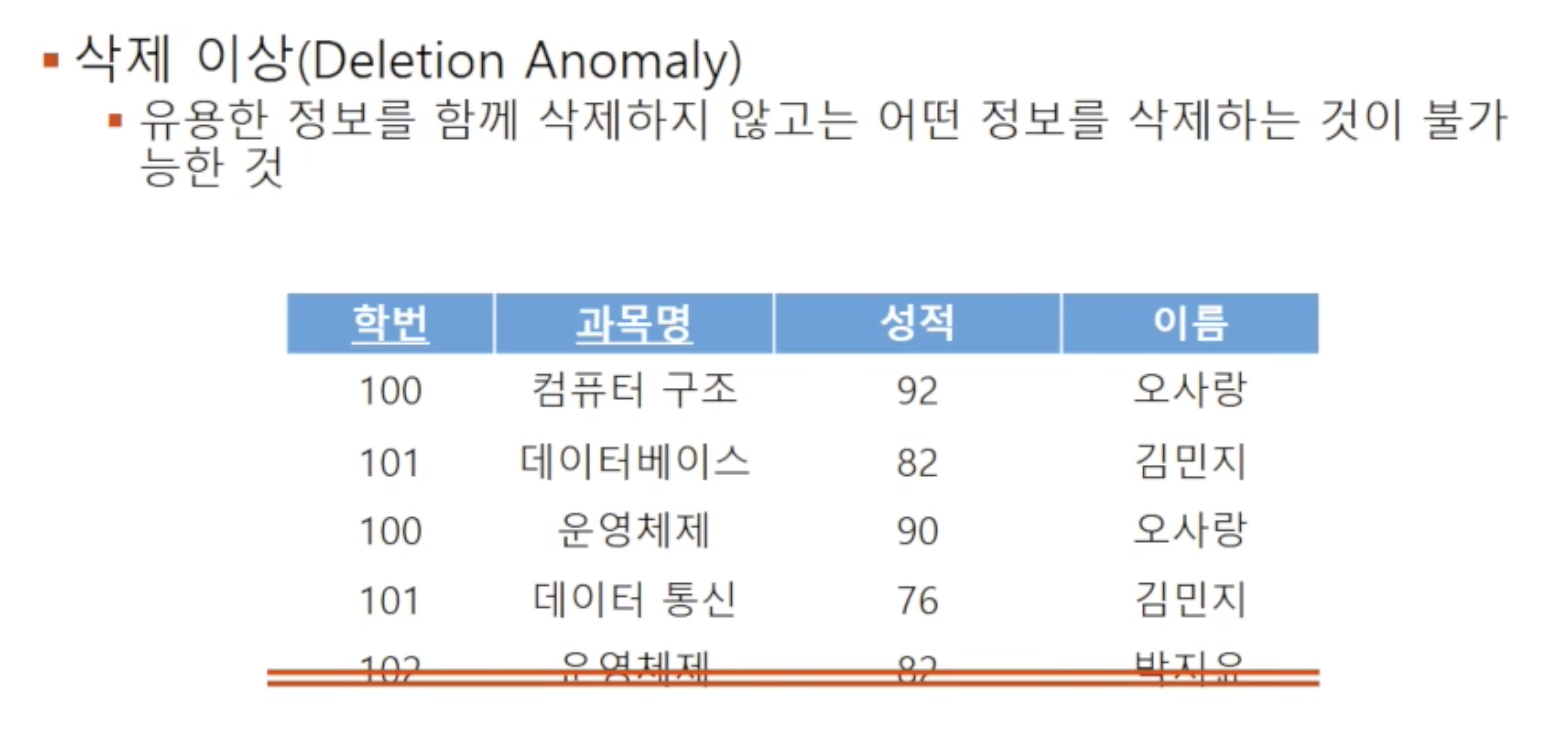
🔘 삭제 이상
유용한 정보를 함께 삭제하지 않고서는 어떤 정보를 삭제하는 것이 불가능한 것을 의미합니다. 위 예시에선 박지윤 학생이 성적을 취소하고 싶어 해당 튜플을 삭제하면, 박지윤 학생에 대한 다른 정보도 같이 손실되는 이상이 발생하게 됩니다
정규화를 통해 relation을 분리하여 중복 데이터를 제거하여 이런 문제들을 방지합니다
🔸 함수종속 (Functional Dependency)
일반적으로 함수라고 하면 입력 값이 주어졌을 때 정해진 출력을 갖게 됩니다. 즉, 입력이 같으면 항상 출력은 같습니다
함수 종속은 이와 유사하게 어떤 Attribute X의 값을 알면 다른 Attribute Y의 값도 유일하게 어떤 값이 되는지 알 수 있는 것을 말합니다. 이 때, "Y는 X에 종속된다" 혹은 "X는 Y를 결정한다"라고 말합니다 (X->Y로 표기). 또한, X를 Y의 결정자(determinant)라고 합니다
함수종속과 이상현상의 연관관계는 다음 섹션인 정규형 예시들에서 확인할 수 있습니다
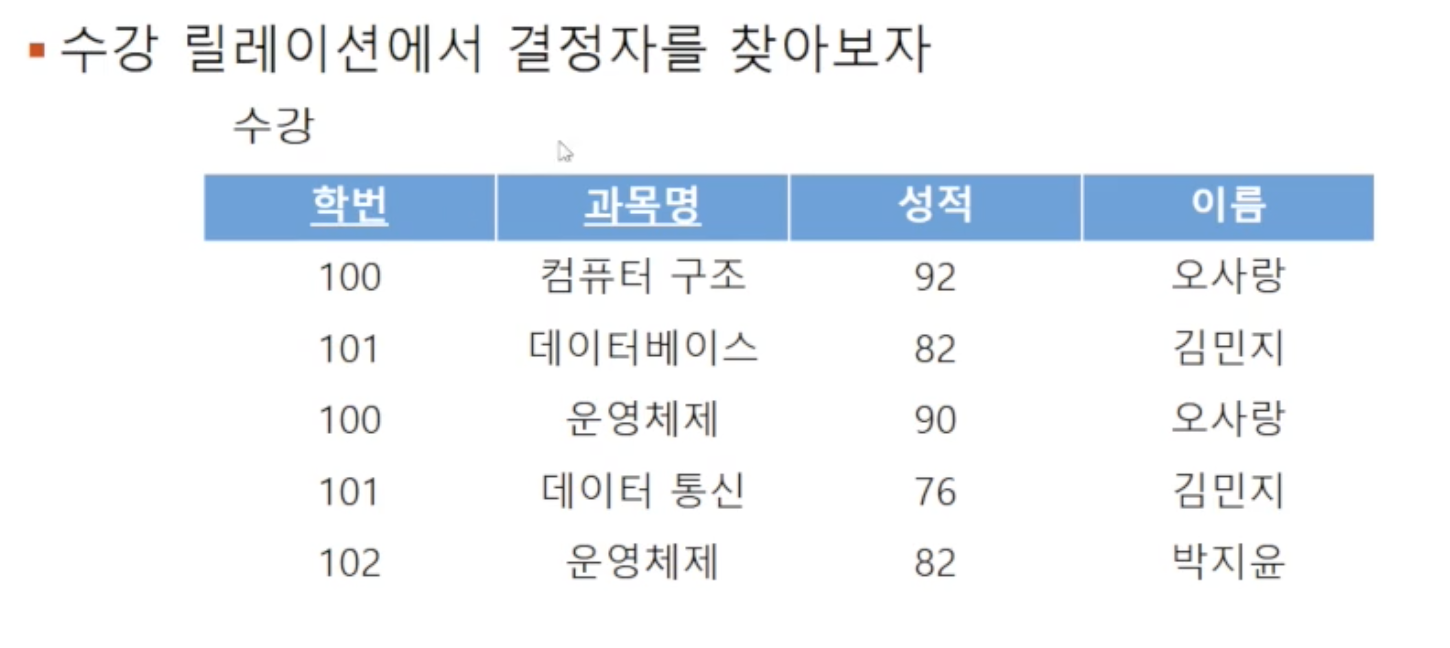
🔘 예시
위 예시에선 학번을 알면 그에 대응되는 유일한 이름을 알 수 있으므로, 이름은 학번에 종속됩니다 (학번->이름). 그리고 학번과 교과명을 알면 그에 따른 성적을 알 수 있으므로, 학번과 교과명은 성적의 결정자입니다 ({학번,과목명}->성적)
🔘 완전 함수 종속(FFD: Full Functional Depedency)
함수 종속의 성질에는 두 가지가 있는데, 먼저 완전 함수 종속은 결정자 Attribute 집합은 통째로만이 결정자가 될 수 있는 경우입니다. 위 예시에선 {학번,과목명}을 모두 합쳐야만 성적의 결정자가 될 수 있고, 과목명 혼자서는 성적의 결정자가 될 수 없기에 완전 함수 종속의 예시입니다
🔘 부분 함수 종속(PFD: Partial Functional Dependency)
결정자가 여러 개의 Attribute로 구성되고, 결정자 집합 전체가 아닌 일부분에도 종속되는 것을 말합니다. 위 예시에서 결정자 집합을 {학번,과목명}으로 묶었을 때 "이름"에 대한 종속성을 판별해보면 집합의 일부인 학번만으로도 종속성을 보이므로 부분 함수 종속입니다. 부분 함수 종속은 중복을 유발하므로 제거하려 노력해야 합니다
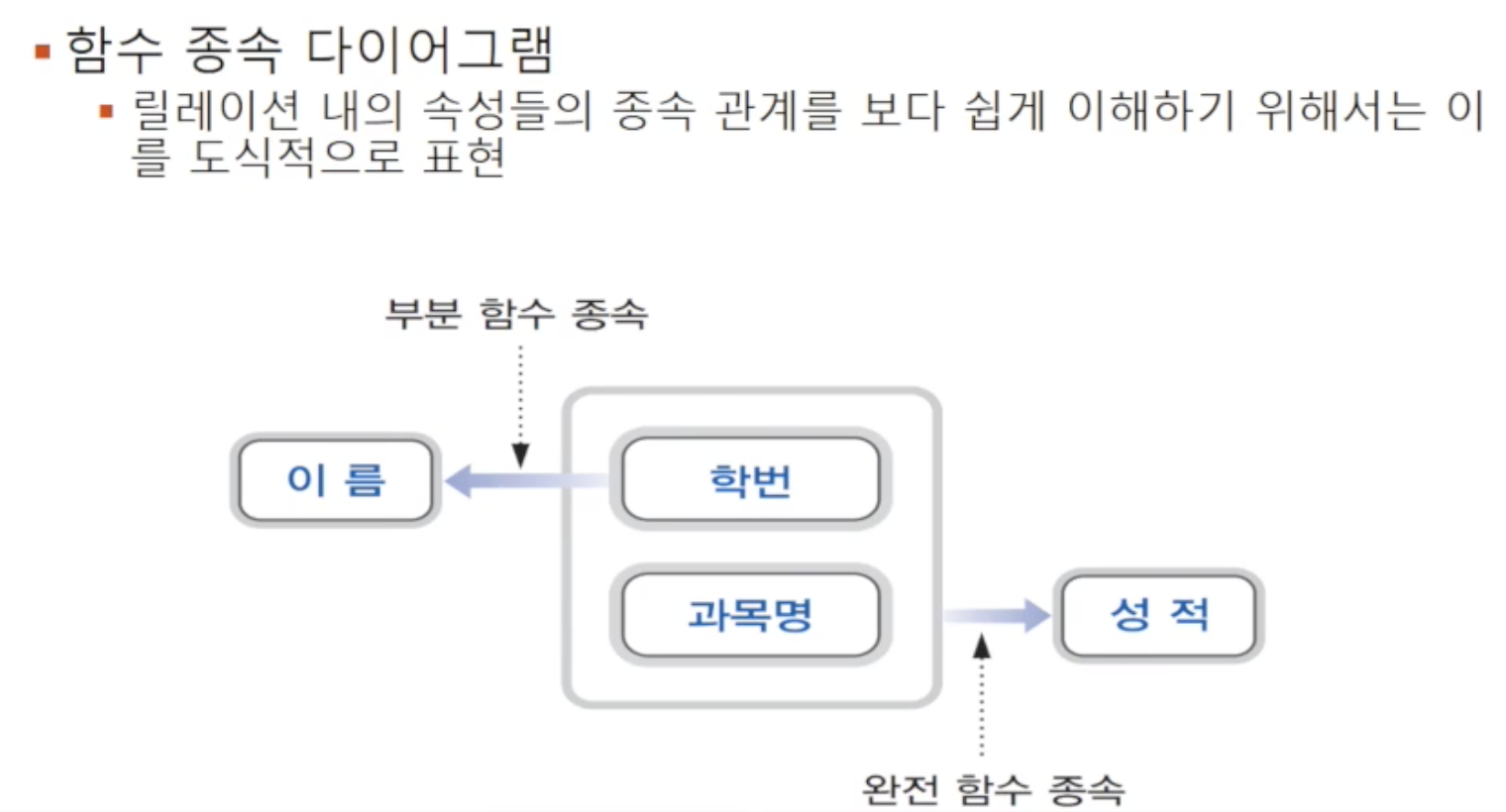
🔘 함수 종속 다이어그램
이런 함수 종속 관계를 도식적으로 표현할 수 있습니다
- Attribute : 작은 직사각형
- 함수 종속성 : 화살표
- 복합 Attribute : 큰 직사각형으로 묶음
🔸 정규형 (NF: Normal Form)

정규형은 정규화에 있어 각 단계마다 어떻게 분해할지에 대한 특정 조건이 존재하고 그 조건을 만족시키는 relation 스키마의 형태를 말합니다. 위 그림에서 제1정규형부터 BCNF까지는 기본 정규형에 포함되고, 제4 제5정규형은 고급정규형에 포함됩니다. 안으로 들어갈수록 요구 조건이 많고 엄격해집니다. 차수가 높은 정규형에 속하는 relation일수록 데이터 중복이 줄어 그에 따른 이상 현상이 발생하는 것을 줄여줍니다
제2정규형이 제1정규형 안에 포함되어 있는 형태를 보면 알 수 있듯이, 제2정규형이란 제1정규형의 조건과 제2정규형의 조건을 모두 만족시켜야 합니다. 모든 relation이 제5정규형까지 될 필요는 없고 특성을 고려하여 적합한 정규형을 선택해서 보통은 기본정규형 BCNF 정도까지 속하도록 정규화합니다
🔸 정규형 단계 : 비정규형

하나의 속성에 여러 개의 값을 가지고 있는 것
🔸 정규형 단계 : 제1정규형
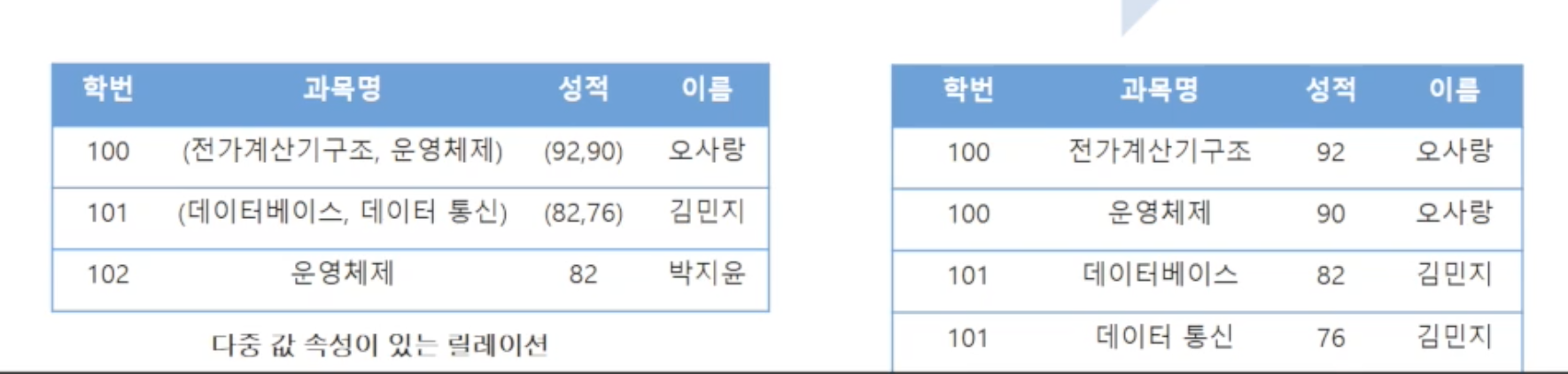
제1정규형을 만족하는 relation는 모든 Attribute의 도메인 값이 atomic해야 합니다. 앞에서 관계형 모델의 속성값은 atomic해야 한다고 했던 것과 같습니다. 위는 다중 값을 갖는 비정규형을 제1정규형으로 정규화하는 예시입니다
하지만 아직 제1정규형 정도로는 이상 현상을 충분히 유발할 수 있는 상태입니다. 그 이유는 위 relation은 부분 함수 종속성을 갖고 있기 때문입니다. "이름"이 기본키인 {학번,과목명} 집합 전체에 완전 조속되지 않고 일부인 학번에 종속됩니다. 이로 인해 오사랑과 김민지는 중복이 발생하여 이상현상을 유발할 수 있습니다
🔸 정규형 단계 : 제2정규형

제2정규형은, 제1정규형 조건을 만족하면서 모든 Attribute가 기본키에 완전 함수 종속하는 것을 말합니다. 위는 부분 함수 종속을 제거하고 모든 속성이 기본키에 완전 함수 종속하도록 relation을 분해하는 예시입니다
🔘 무손실 분해 (nonloss decomposition)
이렇게 relation을 분해할 때는 반드시 정보의 손실 없이 분해해야 합니다. 분해된 relation들을 Natural Join하면 분해 전 relation으로 복원이 가능해야 합니다. 즉, 의미적으로 동등한 relation으로 분해되어야 합니다
🔸 정규형 단계 : 제3정규형
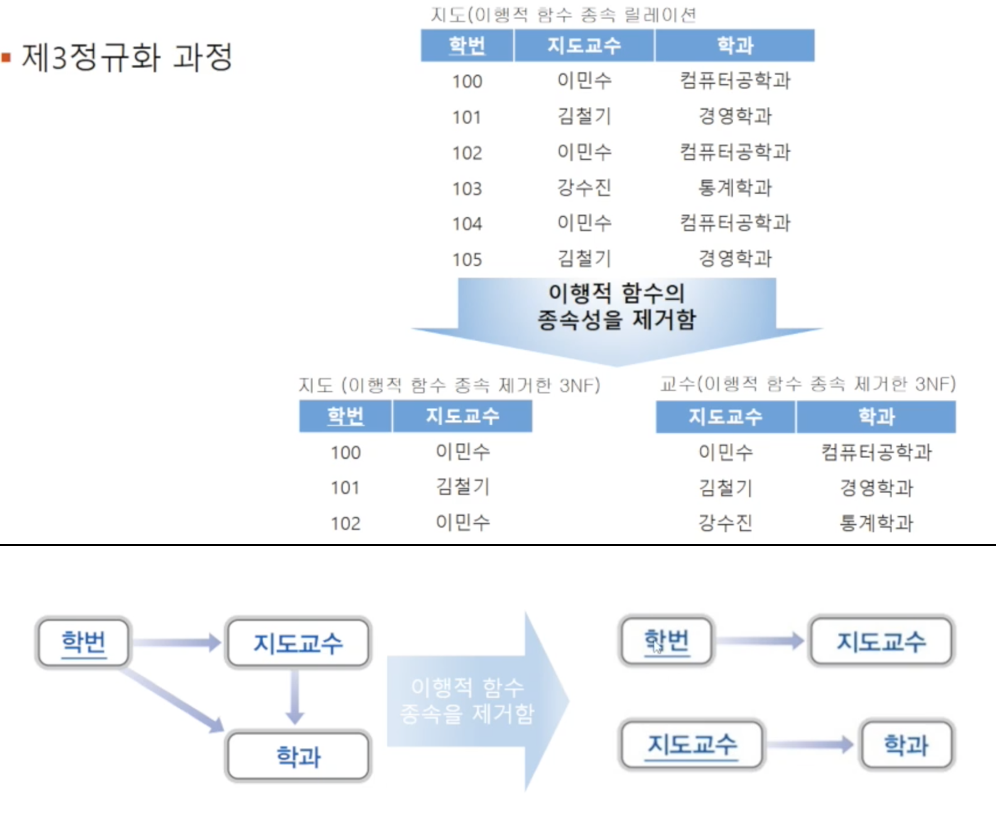
제3정규형은, 제2정규형 조건을 만족하면서 모든 Attribute가 기본키에 이행적 함수 종속이 되지 않는 것을 말합니다. 이행적 함수 종속이란, 3개의 속성에 존재하는 함수 종속을 의미합니다(삼각관계). 예로, A가 B를 결정하고 B가 C를 결정한다면, 결국 A가 C를 결정하게 되는데 이 상황을 이행적 함수 종속이라 합니다. 이처럼 제2정규형을 만족하더라도 하나의 relation에 함수 종속관계가 여러 개 존재하면 이행적 함수 종속이 발생할 가능성이 있고 이상 현상을 유발할 수 있습니다
🔸 정규형 단계 : 보이스/코드 정규형 (Boyce/Codd Normal Form, BCNF)
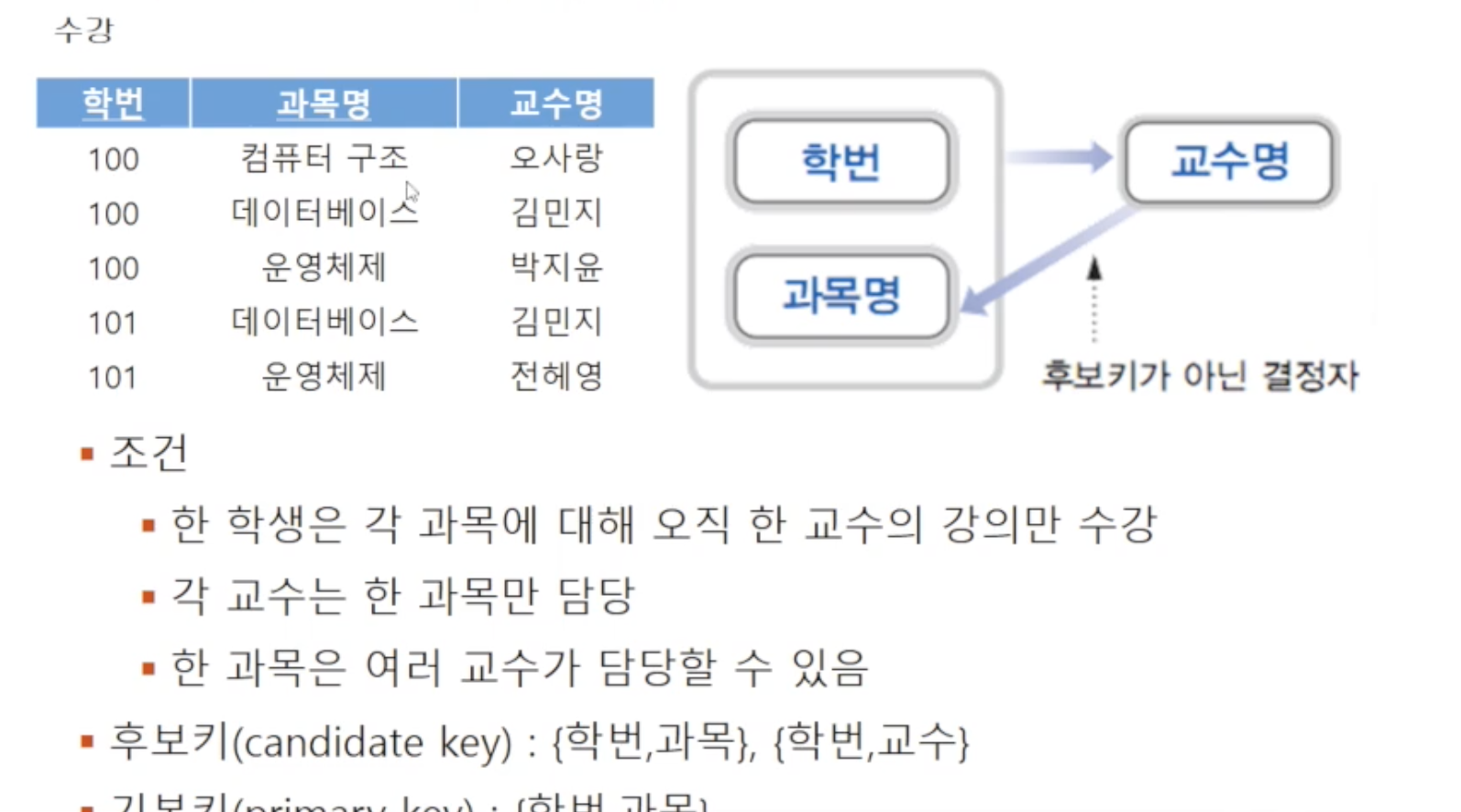
BCNF는, 제3정규형 조건을 만족하면서 모든 결정자(determinant. 종속관계에서의 key)가 candidate key인 경우를 말합니다. 앞에서 살펴봤던 relation들은 모두 candidate key를 하나만 가지고 있어서 바로 기본키로 선정된 경우였지만 실제로는 여러 개의 후보키가 존재할 수 있습니다. BCNF는 제3정규형을 만족하더라도 여러 개의 candidate key가 존재할 경우 이상현상이 발생할 수 있다는 점을 보완한 것입니다 (그래서 strong 3NF라고도 함)
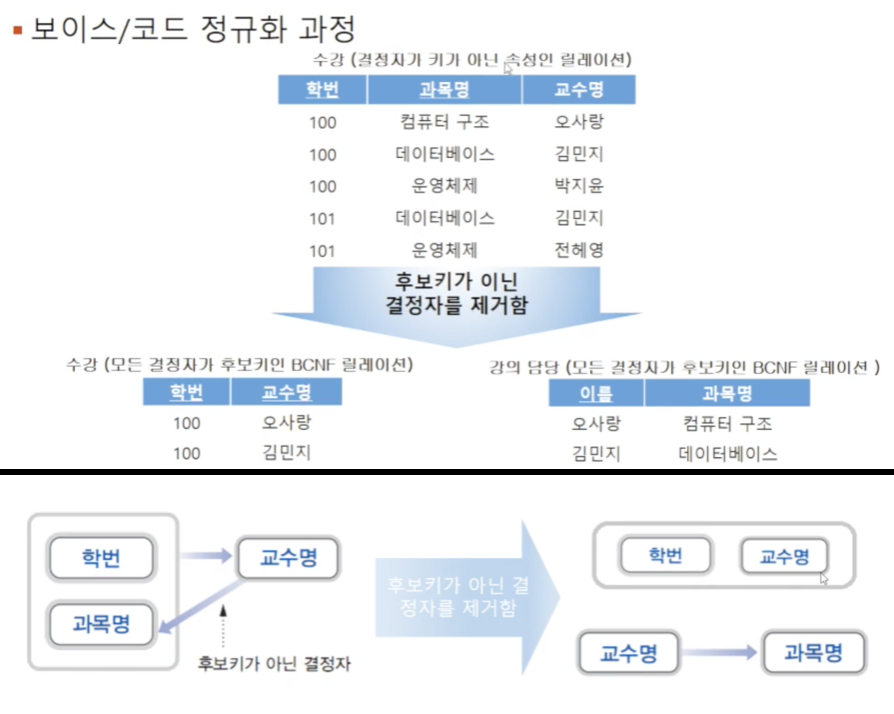
위 예시에서, 추가 조건들에 의해 {학번,과목}이 후보키가 될 수 있으면서 교수명이 결정자가 되는 경우로 제3정규형을 만족하지만 BCNF를 만족하지 않는 상태입니다. BCNF는 문제가 되는 결정자인 교수명을 제거하여 relation을 분리함으로써 정규화합니다
🌀 Indexing
index에 어떤 종류가 있는지와 어떻게 검색을 빠르게 해주는지를 살펴봅니다
🔸 기본개념
우선 index 메커니즘은 원하는 데이터에 접근하는 속도를 높이기 위해 사용됩니다. DB 파일의 index는 책의 index와 동일한 방식으로 동작합니다. index를 사용하면 앞에서부터 순차적으로 찾아가지 않더라도 원하는 데이터가 있는 위치로 이동할 수 있습니다
🔘 용어
search key는 파일에서 레코드를 찾기 위해 사용되는 Attribute 집합입니다index entry는 하나의 search key와 그와 연결된 레코드들의 포인터 쌍으로 구성된 데이터 구조입니다. 이 포인터를 가지고 해당 레코드로의 랜덤 액세스가 가능합니다index file은 index entry들로 구성된 파일로 원본 파일보다는 일반적으로 훨씬 작습니다
🔘 index 대분류
두 가지가 있지만 강좌에서는 ordered index만을 다룹니다
Ordered index: search key를 책의 index처럼 정렬된 순서로 저장하는 것Hash index: search key를 해시함수로 생성하여 저장하는 것
🔸 정렬여부에 따른 분류 : Primary Index
search key의 순서와 실제 파일이 정렬된 순서가 동일한 경우를 말합니다. 순차적으로 정렬된 파일의 순서를 정하는 기준이 되는 Attribute를 search key로 사용하는 index입니다. 같은 데이터끼리 뭉쳐지게 되므로 clustrering index라고도 합니다. 주로 기본키가 search key가 되긴 하지만 꼭 그럴 필요는 없습니다
🔘 Index-sequential file
primary index를 가지고 순차적으로 정렬된 데이터 파일을 말합니다. 즉, search key에 해당하는 Attribute에 대해 순차적으로 정렬되어 있습니다
🔸 정렬여부에 따른 분류 : Secondary index
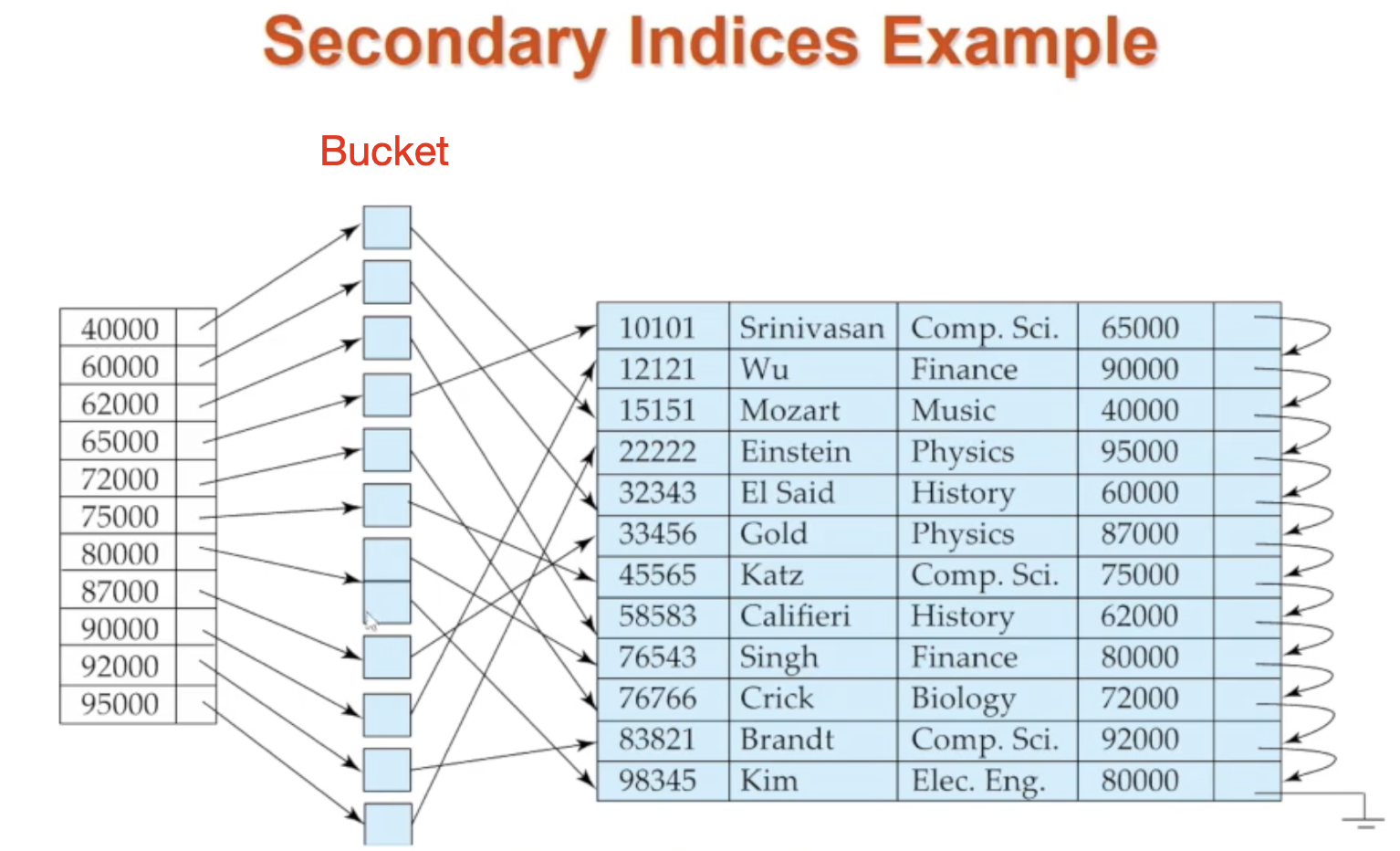
search key의 순서와 실제 파일이 정렬된 순서가 다른 경우를 말합니다. 파일의 순차적 정렬과 다른 정렬을 가지는 search key를 가지는 index입니다. 즉, key의 순서와 레코드 순서가 상관이 없습니다. non-clustering index라고도 불립니다. secondary index를 사용하는 경우 index entry에 저장된 포인터는 특정 레코드가 아닌 모든 실제 레코드 포인터를 가지고 있는 bucket을 가리켜야 합니다
🔸 커버리지에 따른 분류 : Dense Index
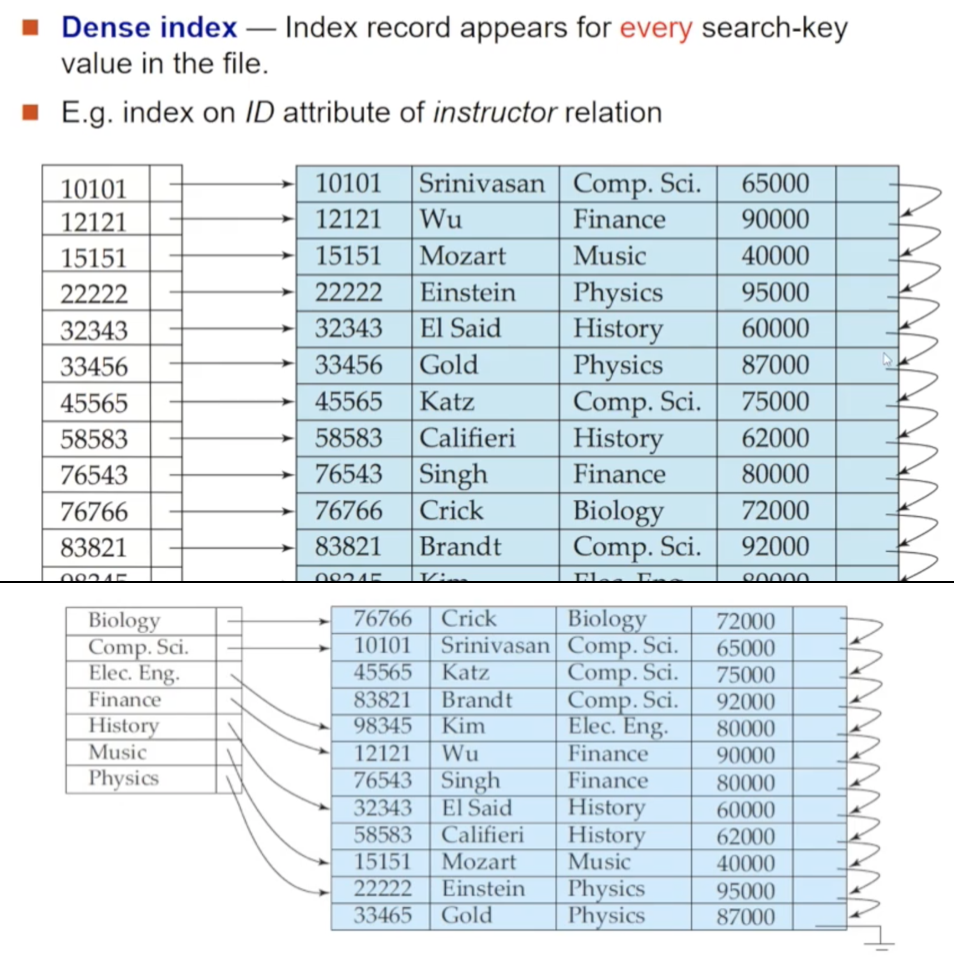
ordered index 파일에는 dense와 sparse 두 가지가 있습니다. 먼저 dense index 파일에는 원본 relation에 존재하는 모든 search key Attribute 값을 가지고 있습니다. 위 예시에서 ID가 32343인 레코드를 찾는다면 우선 index 파일(좌)에서 search key 32343의 포인터를 찾아내어 따라가면 원본 relation(우)에서 레코드를 찾을 수 있습니다
primary/secondary index 모두 가능하지만, dense index 파일의 구성이 서로 다릅니다. 위의 두 번째 사진처럼 primary index여서 clustering이 되어 있는 상태라면 index 파일에는 각 search key당 포인터를 하나씩만 저장하면 됩니다. 반면, clustering이 되어 있지 않은 secondary index라면 모든 레코드들에 대한 일대일 포인터를 가지는 bucket이 있어야 합니다
🔸 커버리지에 따른 분류 : Sparse Index
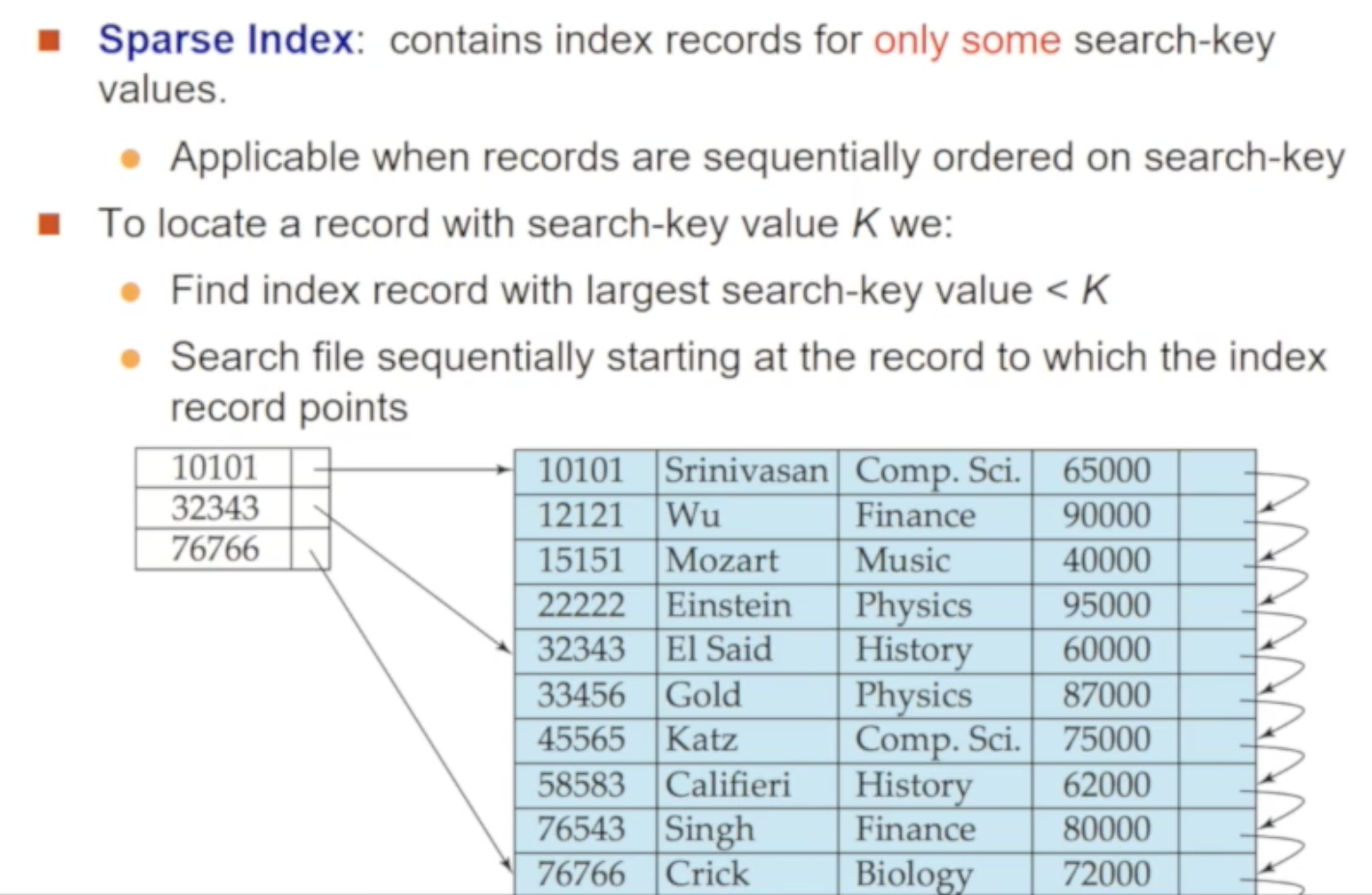
원본 relation의 일부 search key 값만을 저장하고 있는 index 파일을 말합니다 (ex. 위 사진에서 ID:12121,33456 등에 대한 index entry가 없습니다)
예로, 15151을 찾는다면 우선 index 파일을 뒤져 10101과 32343 사이에 있겠거니를 확인합니다. 10101에 저장된 포인터로 이동하여 32343이 나올 때까지 한칸씩 아래로 이동하며 15151을 찾아나갑니다. 이런 특징으로 sparse index 파일을 사용하려면 반드시 primary index를 사용하여 원본 relation 정렬되어 있어야 합니다
🔸 Multi-level Index
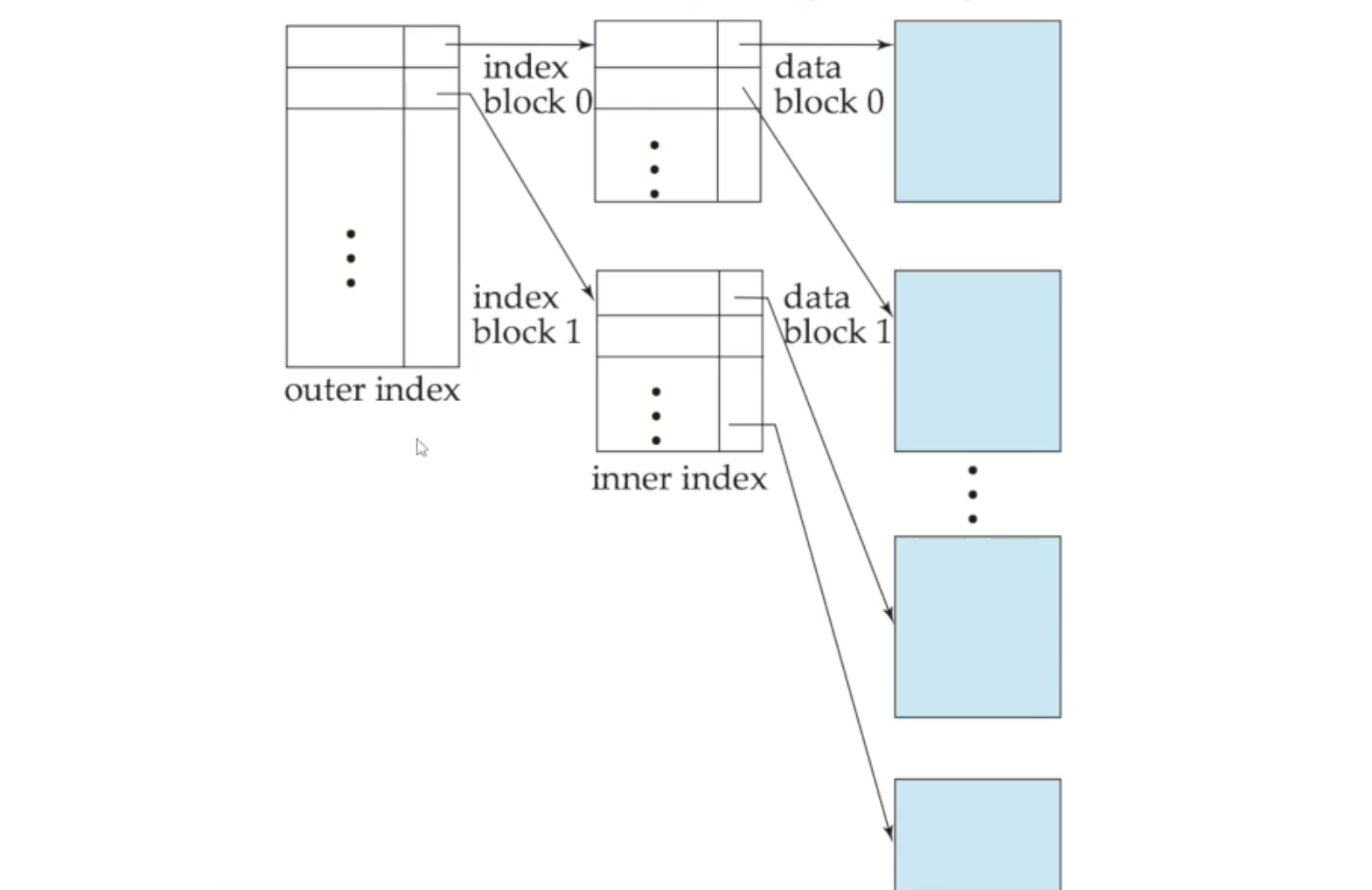
만약 index 파일이 커서 (특히 primary index) 전체를 한 번에 메모리에 유지할 수 없다면, 디스크와의 상호작용이 필요하므로 검색비용이 많이 들게 됩니다
디스크 상호작용을 최소화하기 위해 index 파일 자체를 한번 더 indexing하는 방법이 있습니다. 기존 primary index 파일을 순차파일로 취급하여 inner index로 정의하고, 그에 대한 sparse index를 만들어 inner index로 정의합니다. 만약 이렇게 해도 outer index를 메모리에 한번에 올릴 수 없다면, 한번 더 indexing해줄 수 있습니다
🔸 B+ Tree
B+Tree는 indexed-sequential file의 문제점을 해결하기 위해 만들어진 index입니다
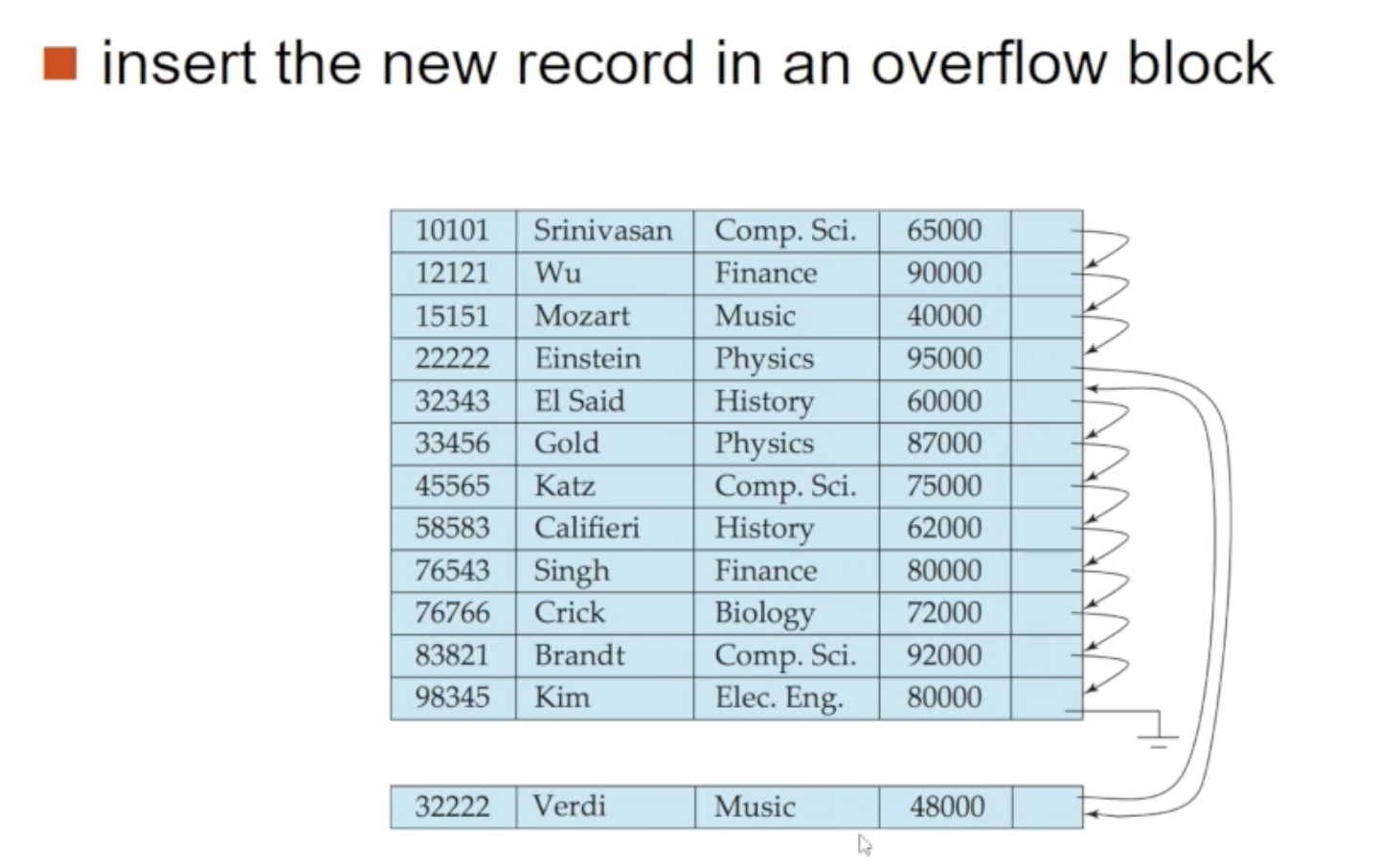
🔘 indexed-sequential file의 문제점
indexed-sequential file은 search key를 기준으로 정렬이 되어 있고 이를 유지해야 합니다. 이 정렬을 유지하기 위해선 하나의 레코드를 삽입/삭제하더라도 많은 양의 레코드를 이동시켜야 하므로 막대한 비용이 듭니다
그래서 대안으로 위 사진에서 보이는 overflow block이란걸 사용합니다. 32222-Verdi라는 레코드를 삽입하는데 전체 relation을 이동시키는게 아닌 overflow block에 넣습니다. 그리고 2222-Einstein의 next 레코드 참조값을 새로이 할당한 overflow block을 가리키게 만듭니다
이렇게 overflow block을 사용하면 새로운 레코드를 빠르게 삽입할 수 있지만 search key 순서와 물리적 순서가 일치하지 않아 성능이 많이 떨어지게 됩니다. 그래서 주기적으로 전체 파일을 재구성 해주어야 한다는 단점을 갖고 있습니다
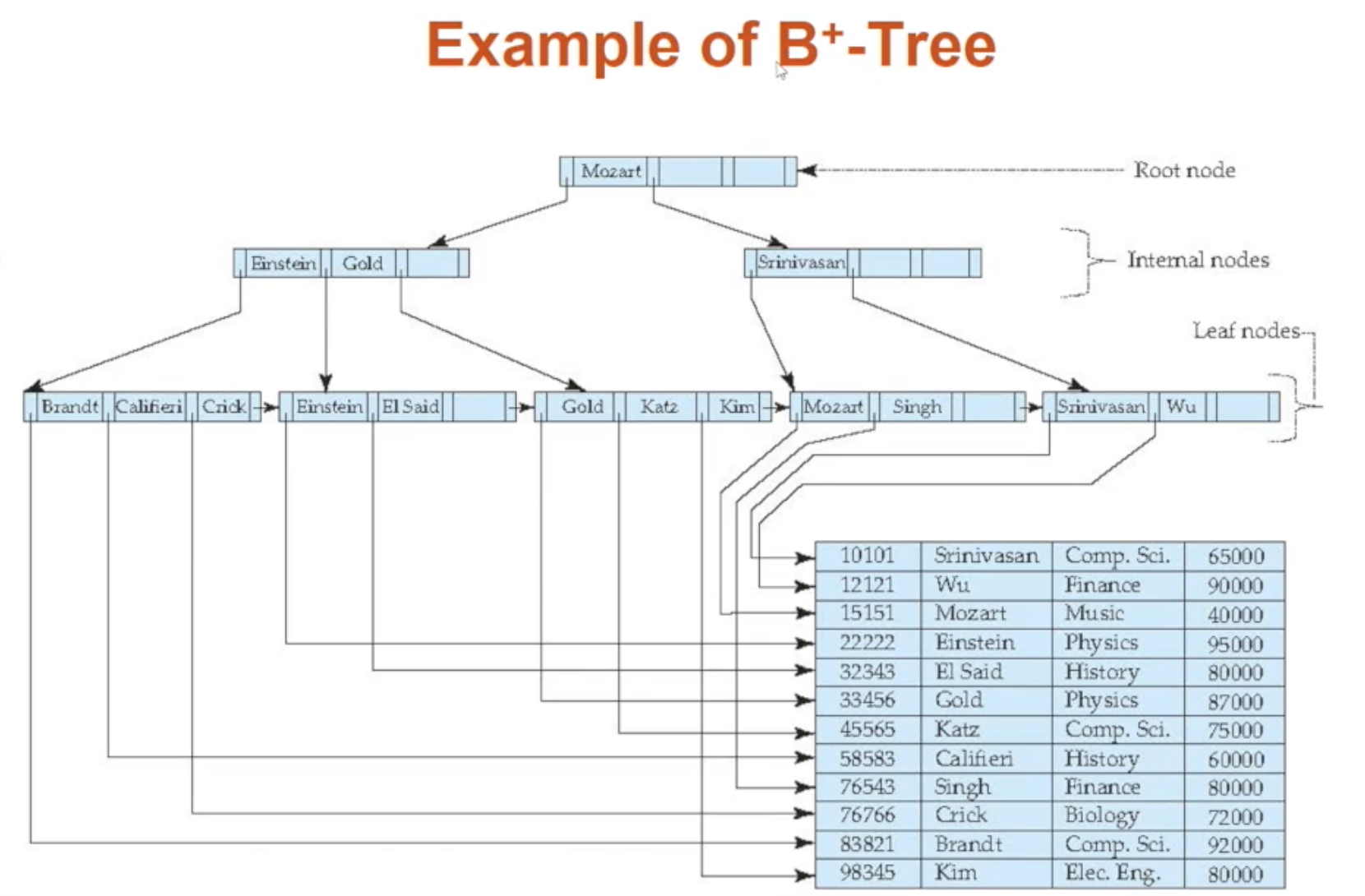
🔘 B+ Tree의 전체적인 구조
반면, B+ Tree를 사용하면 삽입/삭제가 발생하더라도 상대적으로 적은 양의 비용으로 재구성이 가능합니다. 마이너한 단점으로 추가적인 삭제에 따른 오버헤드와 메모리 공간적인 오버헤드가 더 들긴 합니다. 이런 단점보다 장점이 훨씬 뛰어나므로 B+ Tree는 광범위하게 사용되고 있습니다
위 사진은 B+ Tree의 전체적인 구조로 root, internal, leaf 노드로 이루어져 있습니다. 그리고 balanced tree이므로 root로부터 leaf로 가는 length가 동일합니다 (balanced tree는 루트를 기준으로 왼쪽 트리와 오른쪽 트리의 높이 차이가 1이하거나 같은 트리를 말합니다). root와 internal 부분은 sparse index가 되고, leaf는 데이터를 가리키는 dense index가 됩니다
B+ Tree는 root를 가지는 rooted tree입니다. 그리고 다음과 같은 속성을 만족합니다. 아래에서 n은 하나의 노드가 가진 자식으로의 포인터 혹은 레코드로의 포인터 개수를 의미합니다
- balanced tree로써 root -> leaf까지의 length가 모두 동일합니다
- root/leaf를 제외한 internal 노드가 가질 수 있는 자식의 개수는 [n/2]와 n 사이입니다
- leaf가 가지는 값의 개수는 [(n-1)/2]와 n-1 사이입니다
- 그 외 특이 케이스
- root가 leaf가 아니라면, 최소 2개 이상의 자식을 가져야 한다
- root가 leaf라면, 가지는 값의 개수는 0과 (n-1) 사이입니다

🔘 B+ Tree 노드 구조
root/internal/leaf 노드 모두 동일한 구조를 가집니다. P는 자식 노드로의 포인터 혹은 실제 레코드로의 포인터를 의미하고, K는 search key 값을 의미합니다. K는 무작위가 아니라 정렬이 되어 있습니다 (K1이 가장 작고 Kn-1이 가장 큼)

🔘 Leaf 노드
leaf 노드가 가진 포인터들은 파일 레코드를 가리키고 있습니다. 포인터 Pi는 파일 레코드를 가리키며, 바로 뒤에 붙은 Ki는 Pi가 가리키는 파일 레코드의 search key 값을 가지고 있습니다
하나의 leaf 노드 내에서 P와 K들은 순서에 맞게 정렬되어 있으며, leaf 노드들 간에도 순서 정렬이 되어 있습니다 (leaf노드1은 leaf노드2보다 search key 값이 작다). 그리고 마지막 포인터인 Pn은 search key 순을 다음 leaf노드를 가리킵니다. 각 leaf 노드는 search key를 기반으로 순서대로 놓여있고 이 정렬을 위해 Pn을 사용합니다
이러한 정렬 덕에 연속적으로 파일을 처리할 때 능률적일 수 있습니다. 반면, 실제 레코드들은 정렬을 신경쓸 필요가 없어 삽입/삭제를 위한 레코드 재구성에 비용이 크다던지 overflow block을 사용하지 않아도 됩니다

🔘 non-Leaf 노드
non-Leaf 노드는 leaf 노드에 대한 multi-level sparse index를 이루고 있습니다. non-Leaf 노드는 포인터 P가 레코드가 아닌 자식 노드로의 포인터가 들어 있다는 점을 제외하면 leaf 노드와 동일한 구조를 가집니다
Pi가 가리키는 자식노드의 모든 search key값은 Ki보다 작아야 합니다 (즉, 왼쪽부터 오름차순). 위 그림에서 P2가 가리키는 자식노드의 모든 search key값은, K1보다는 크거나 같고 K2보다는 작거나 같아야 합니다

🔘 B+ Tree 유의사항(Observation)
-
internal 노드는 포인터로 이루어져 있어 논리적으로 근접한 블록이 물리적으로 근접할 필요는 없습니다. 어떤 노드가 바로 옆의 leaf 노드라고 해서 디스크 상에서 물리적으로 바로 옆에 있을 필요는 없고 다른 부분에 저장되어도 무관합니다
-
B+ Tree의 non-Leaf 노드는 sparse index 계층을 이루게 됩니다
-
B+ Tree는 비교적 적은 수의 계층을 가지고 있습니다. search key의 개수가 K개라면, tree의 높이는 logn/2를 넘지 않습니다. 즉, 계층을 따라 내려가는데 있어 검색속도를 크게 저하시키지 않습니다
-
삽입/삭제가 발생하더라도 index가 log시간 내에 재구성될 수 있으므로 효과적으로 처리할 수 있습니다
-
데이터를 변경하면 그에 따라 index 갱신도 오버헤드로 발생합니다. 많은 레코드를 갱신한다면 index 갱신시간도 많이 걸리므로 반드시 index를 많이 가지고 있다고 해서 훌륭한 DB는 아닙니다
🌀 Transaction
🔸 트랜잭션이란?
🔘 구성
트랜잭션은 DB에서 매우 중요한 개념 중 하나로 DBMS에서 데이터를 다루는 논리적인 작업의 단위입니다. 하나의 트랜잭션은 여러 개의 데이터 연산으로 구성되어 있습니다. 구체적으론, 여러 개의 연산이라 할 수도 있고 SQL에서 하나의 연산을 두 DB의 relation에 접근해서 양쪽에 동일하게 반영시킬 때도 트랜잭션으로 묶어주게 됩니다. 일반적으로는 하나의 SQL문을 하나의 트랜잭션으로 보지만 실제로는 여러 개의 SQL문으로 이루어진 트랜잭션도 존재합니다
🔘 목적/용도
DB에서 이런 트랜잭션을 정의하는 이유는 데이터 작업 중 장애가 발생할 때 데이터를 복구하는 작업의 단위로 사용하기 위함입니다. 데이터 작업 중 장애가 발생해서 트랜잭션을 제대로 수행하지 못했다면 그 트랜잭션이 일어나기 전 상태로 보류시켜야 하는데, 이 복구 시점을 어디까지로 잡을 것이냐에 대한 기준을 트랜잭션으로 잡는 것입니다. 따라서 하나의 트랜잭션 내 연산들은 전부 수행되거나 전혀 수행되지 않아야 합니다 (all or nothing). 그리고 여러 작업이 동시에 같은 데이터를 다룰 때 작업을 서로 분리하기 위한 단위로 사용되기 위함도 있습니다.
🔸 트랜잭션의 성질
트랜잭션은 4가지 성질을 가지고 있습니다
🔘 원자성(Atomicity)
all or nothing을 의미합니다. 하나의 트랜잭션에 포함된 작업들은 전부 수행되거나 전혀 수행되지 않아야 합니다. 트랜잭션 수행 도중 오류가 발생하면, 일부만 수행되는 일이 없도록 DBMS의 회복 모듈을 사용하여 원자성을 보장합니다
🔘 일관성(Consistency)
기본적으로 데이터들은 항상 일관성을 가져야 함을 말합니다. 다만, 트랜잭션 도중에는 일시적으로 일관되지 않을 수 있습니다. 트랜잭션이 수행되거 전에도 일관적인 상태를 가져야 하고, 트랜잭션 후에도 새로운 일관된 상태를 유지해야 합니다
예로, 계좌이체 전에는 A(100만원)/B(50만원)이라는 일관된 상태이며, 트랜잭션 중에는 일시적으로 A(100만원)/B(100만원)이라는 일관되지 않은 비정상적인 상태였다가, 트랜잭션이 완료되면 A(50만원)/B(100만원)이라는 새로운 일관된 상태가 됩니다
🔘 고립성(Isolation)
한 트랜잭션이 데이터를 갱신하는 동안 다른 트랜잭션이 이 데이터에 접근하지 못하게 막아야 합니다. 다수의 트랜잭션이 동시에 수행되더라도 그 결과가 순차적으로 수행된 것과 같음을 보장하는 DBMS의 동시성 제어 기능이 고립성을 보장합니다
🔘 지속성(Durability)
성공적으로 완료된 트랜잭션은 변경한 데이터를 영구히 저장해야 합니다. 한번 commit이 되면 그 데이터는 DB에 영구적으로 저장되어야 합니다. 트랜잭션은 아래와 같은 상태 과정을 거칩니다
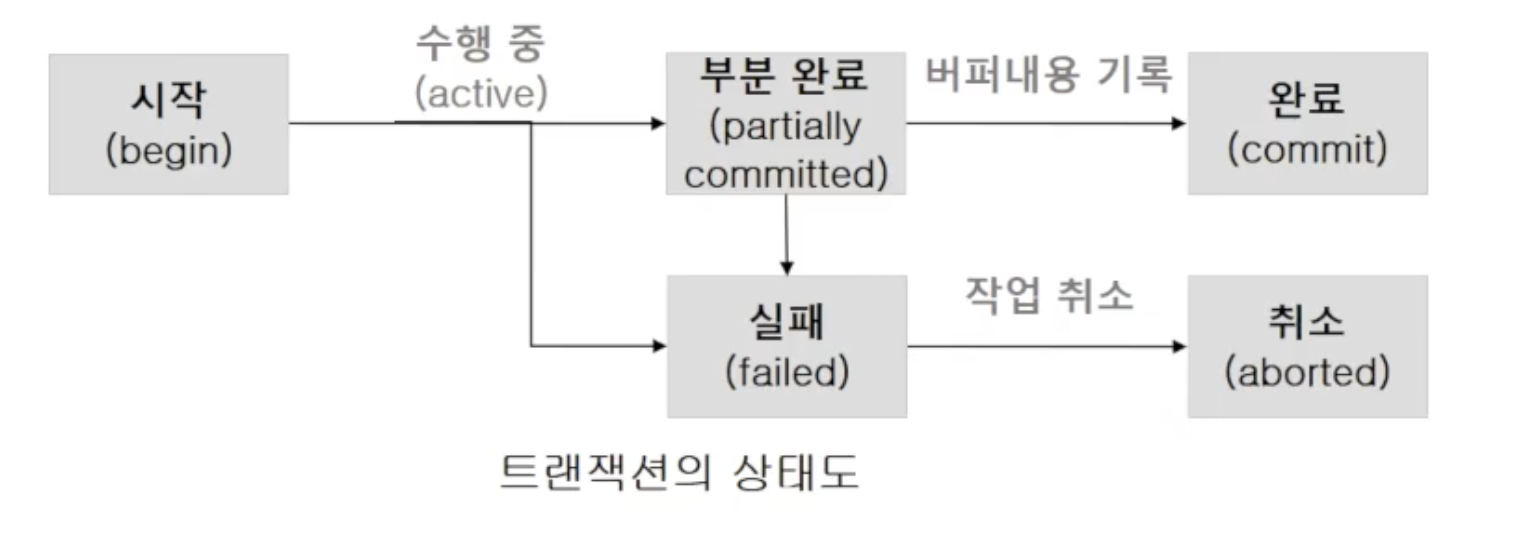
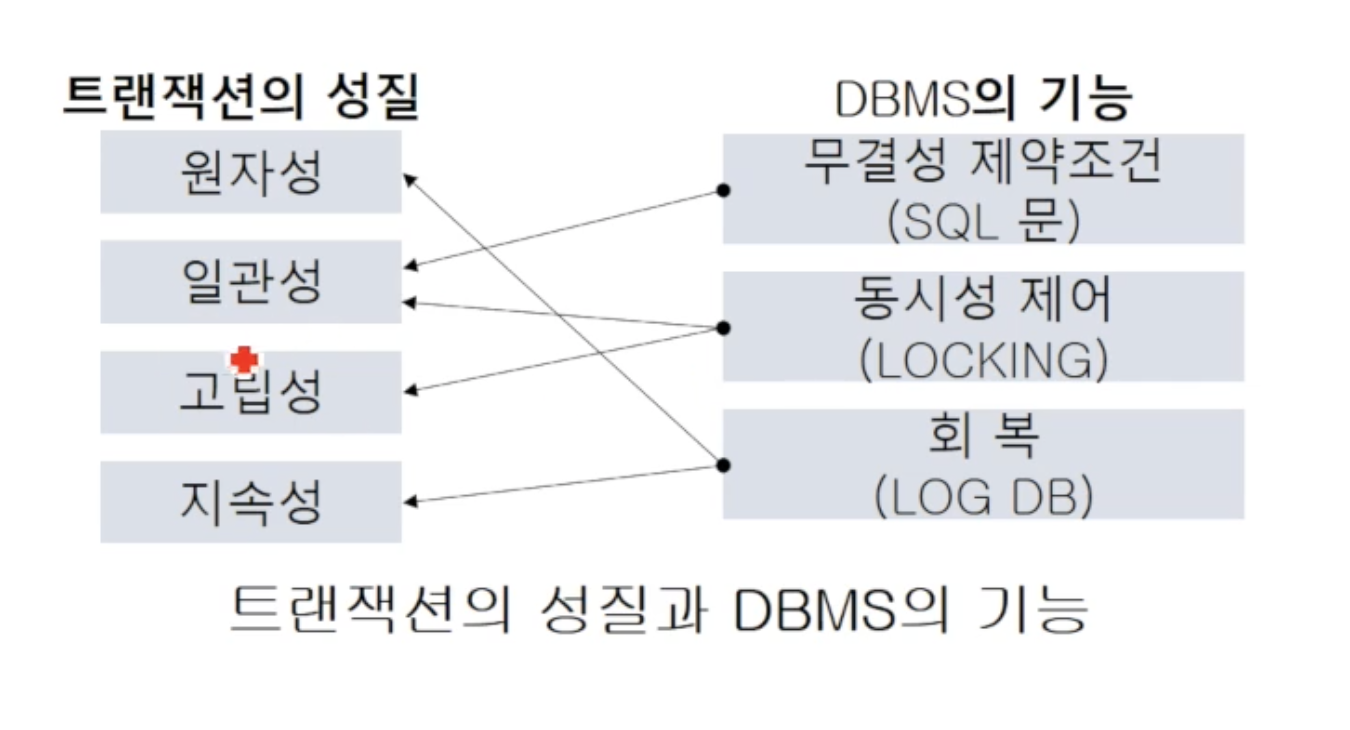
참고로, 무결성 제약조건은 어떤 권한을 가진 사용자가 실수로 데이터 일관성을 헤치는 것을 막기 위해 존재합니다 (ex. 은행잔고는 양수여야 한다, 학생ID는 기본키다)
이러한 속성들을 유지하기 위해 DBMS는 아래와 같이 2가지 기능을 가집니다
🔸 DBMS기능 : 회복
트랜잭션이 데이터를 갱신하는 도중에 시스템이 고장나도 데이터 일관성 유지를 위해 복구시켜주는 기능입니다
🔸 DMBS기능 : 동시성 제어
대부분의 DBMS는 다수의 사용자를 가지므로, 동일한 테이블에 여러 사용자가 동시에 접근하기도 합니다. 데이터 일관성 유지를 위해서라면 동시접근 자체를 막으면 되겠지만, 성능을 고려하면 가능한 한 동시접근을 허용하는 것이 필수적입니다. 동시성 제어 기법은 여러 사용자들이 다수의 트랜잭션을 동시에 수행하는 환경에서도, 트랜잭션들 간 간섭이 생기지 않도록 하여 일관성을 보장하는 기능입니다
동시성 제어를 하는 방법에는 대표적으로 "Lock-based 프로토콜"과 "Timestamp-based 동시성 제어"가 있습니다
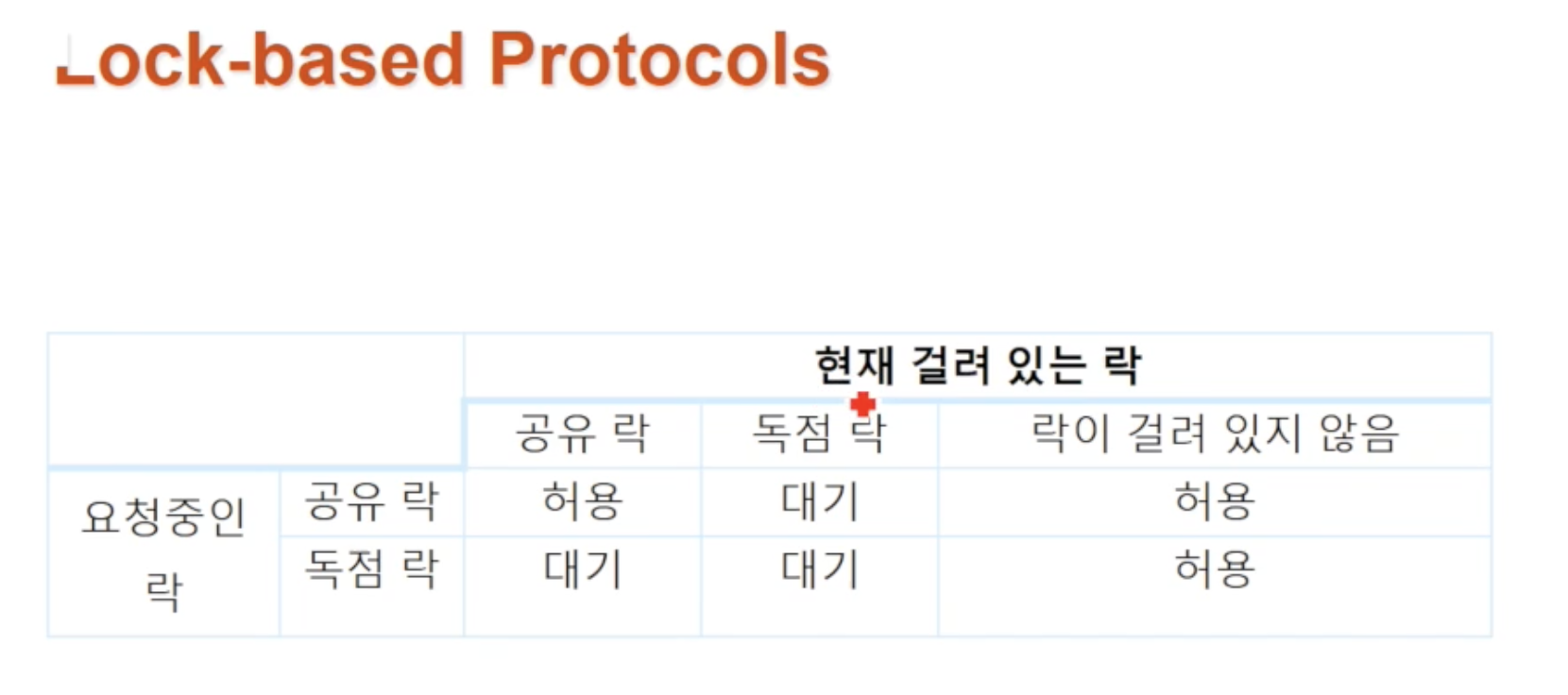
🔘 방법1: Lock-based 프로토콜
널리 사용되는 locking 개념을 사용한 방법입니다. 어떤 트랜잭션이 해당 데이터 갱신을 목적으로 접근할 때는 독점락(X-lock, eXclusive lock)을 요청하고, 읽기를 목적으로 접근할 때는 공유락(S-lock, Shared lock)을 요청합니다. 위 테이블에 명시된 것처럼, 공유락끼리는 서로의 공존을 허용하지만, 독점락은 다른 어떤 락과도 공존을 허용하지 않습니다
이후 해당 데이터 항목에 대한 접근이 끝나면 unlock하여 다른 트랜잭션이 사용할 수 있도록 합니다. 여기서 Lock 정보는 DB 내 각 데이터 항목과 연관된 하나의 변수이며 Lock 테이블 등에 유지됩니다
🔘 방법2: Timestamp-based 동시성 제어
여기서는 락을 걸지 않고 타임스탬프를 사용하여 트랜잭션을 안전하게 다룹니다. 모든 트랜잭션은 시작할 때 고유한 타임스탬프를 가지며, 나중에 시작한 트랜잭션이 더 큰 타임스탬프 값을 가집니다. 두 트랜잭션 내 작업들이 충돌했을 때 이 타임스탬프를 기준으로 어떤 작업이 먼저 수행되어야 하는지 판단합니다. DB의 각 데이터는 각각 RTS(Read timestamp)와 WTS(Write timestamp)를 가집니다. RTS는 해당 데이터를 누군가 읽을 때마다 갱신되고, WTS는 쓰기할 때마다 갱신됩니다
어떤 트랜잭션 Ti가 데이터 D를 읽겠다고(Read) 요청하면, Ti의 스탬프와 D에 적힌 WTS를 비교합니다 (RTS가 아님)
- Ti의 스탬프가 D의 WTS보다 크거나 같다면(=읽기가 마지막 쓰기보다 나중이라면) 작업을 허용합니다
- Ti의 스탬프가 D의 WTS보다 작다면 읽기 이후에 데이터가 수정된 것이므로 거부합니다. 작업이 끝나면 해당 데이터의 RTS를 업데이트합니다
어떤 트랜잭션 Ti가 데이터 D를 쓰겠다고(Write) 요청하면, Ti의 스탬프와 D에 적힌 RTS/WTS를 모두 확인합니다
- Ti가 RTS보다 작다면 누군가 미래 시점에 이미 데이터를 읽어버렸으므로 갱신할 수 없어 거부합니다
- Ti가 WTS보다 작다면 누군가 미래 시점에 이미 데이터를 갱신해버렸으므로 거부하고 Ti가 했던 작업을 전부 롤백합니다
- 그 외 경우에는 쓰기 작업이 가능합니다
