문제 설명
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.
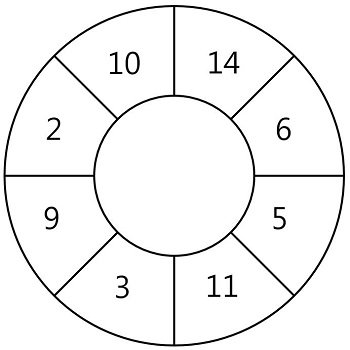
원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.
예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.
제한 사항
- 입력으로 주어지는 sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
- sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
- 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.
문제 해결에 필요한 정보는?
우선 문제를 조금 더 단순하게 만들기 위해 '원형'이라는 조건을 잠시 무시하고 어떻게 접근하면 좋을지 고민해 보겠습니다.
일렬로 연결된 n개의 스티커를 고려했을 때 최적해를 어떻게 구할 수 있을까요. 최종적인 해답의 형태를 분류하자면, 단순하게 (1) n번째 스티커가 포함되느냐, (2) 안되느냐로 나눌 수 있습니다.
- n번째 스티커가 해답(뜯어낸 스티커)에 포함되는 경우
- n - 1번째 스티커는 해답에 포함될 수 없기 때문에, 1 ~ (n - 2)번째 스티커까지 고려했을 때의 최적해와 n번째 스티커가 지닌 값의 합이 최종적인 해답이 됩니다.
- n번째 스티커가 해답에 포함되지 않는 경우
- n - 1번째 스티커가 해답에 포함될 수 있기 때문에, 1 ~ (n - 1)번째 스티커까지 고려했을 때의 최적해가 최종적인 해답이 됩니다.
위와 같이 정리했을 때, 전체 문제 혹은 어떤 부분 문제를 해결하고자 할 때 필요한 정보는 단지 더 작은 부분문제의 최적해뿐임을 알 수 있습니다.
달리 말하면, 1 ~ i번째 스티커까지 고려했을 때의 해답을 결정하는 요소는 1 ~ (i - 2)번째, 그리고 1 ~ (i - 1)번째 스티커까지 고려했을 때의 최적해 뿐이라는 것입니다. 그렇기 때문에 데이터로 위의 최적해들만 캐싱해 둔다면 더 큰 부분문제, 나아가 최종적인 해답을 구할 수 있습니다.
만약, 단순히 작은 문제의 최적해 뿐 아니라, 어떻게 답을 구했는지에 대한 부가적인 정보가 더 큰 문제의 해를 구하는 데 영향을 미친다면, 더 큰 해를 구하는 데 영향을 미치는 모든 추가적인 정보와 그 때의 해답을 캐싱할 효율적인 방법을 따로 찾아야 합니다.
다음과 같이 해답 y를 구하는 데 필요한 독립변수들(x1, x2, ...)을 식별하여 캐싱하기 용이한 경우 해답을 완전탐색보다 훨씬 효율적으로 구할 수 있습니다.(DP)
( x1, x2, x3, ... ) -> y
만약 위와 같은 형태의 캐싱자체가 어렵거나 비효율적이라면 완전탐색으로 문제를 해결해야 하거나, 다른 방식의 접근이 필요합니다.
이 문제에서는 다행히, 부분 문제 혹은 전체 문제를 해결하는 데 필요한 정보가 단순하므로 각 부분 문제의 최적해를 적절히 기록해 놓고 이용하는 것으로 충분합니다.
'일렬로 연결된' 스티커를 가정하면 i - 1번째 스티커까지 고려했을 때의 최적해 하나와, i - 2번째 스티커까지 고려했을 때의 최적해 하나씩을 이용하면 되지만 문제의 '원형으로 연결된' 스티커를 고려하면 조금의 변형이 필요합니다
처음에 최종 해답을
(1) n번째 스티커가 해답에 포함되는 경우
(2) n번째 스티커가 해답에 포함되지 않는 경우
로 나누었는데, 경우 (1)에서는 단순히 1 ~ (n - 2)번째 스티커를 고려했을 때의 최적해가 아니라, 1 ~ (n - 2)번째 스티커를 고려하면서 1번 스티커가 포함되지 않는 부분 최적해가 필요합니다.
그런데 이는 결국, 2 ~ (n - 2)번째 스티커를 고려했을 때의 부분 최적해이므로, 이 값과 n번째 스티커가 지닌 값의 합이 경우 (1)의 해가 됩니다.
경우 (2)에서는 처음 정리한 바와 마찬가지로 1 ~ (n - 1)번째 스티커까지 고려했을 때의 최적해가 경우 (2)의 해가 됩니다.
경우(1)의 해와 경우(2)의 해 중 최댓값이 전체 문제의 최종해입니다.
다시 정리하면,
경우 (1)에서는 2번 스티커부터 n번 스티커가 고려되어야 하고,
경우 (2)에서는 1번 스티커부터 n - 1번 스티커가 고려되어야 합니다.
따라서 일렬로 연결된 스티커 두 줄을 다음과 같이 상상하고
(1) 1번 ~ n - 1번 스티커까지 일렬로 연결된 경우
(2) 2번 ~ n번 스티커까지 일렬로 연결된 경우
각 경우에서 구해지는 해답 중 최댓값을 최종해로 return 하면 됩니다.
코드
import java.util.*;
class Solution {
public int solution(int sticker[]) {
int answer = 0;
int[] dp = new int[sticker.length];
if(sticker.length == 1) return sticker[0];
//1번 스티커(sticker[0])가 고려되는 경우 = n - 1번째 스티커까지 고려
dp[0] = sticker[0];
dp[1] = Math.max(sticker[1], dp[0]);
for(int i = 2; i < sticker.length - 1; i++){
dp[i] = Math.max(dp[i - 2] + sticker[i], dp[i - 1]);
}
answer = dp[sticker.length - 2];
//1번스티커가 고려되지 않는 경우(= 2번 스티커(sticker[1])부터 고려되는 경우) = n번 스티커까지 고려
dp[0] = 0;
dp[1] = sticker[1];
for(int i = 2; i < sticker.length; i++){
dp[i] = Math.max(dp[i - 2] + sticker[i], dp[i - 1]);
}
answer = Math.max(answer, dp[sticker.length - 1]);
return answer;
}
}