리트코드 105번 Construct Binary Tree from Preorder and Inorder Traversal (python)

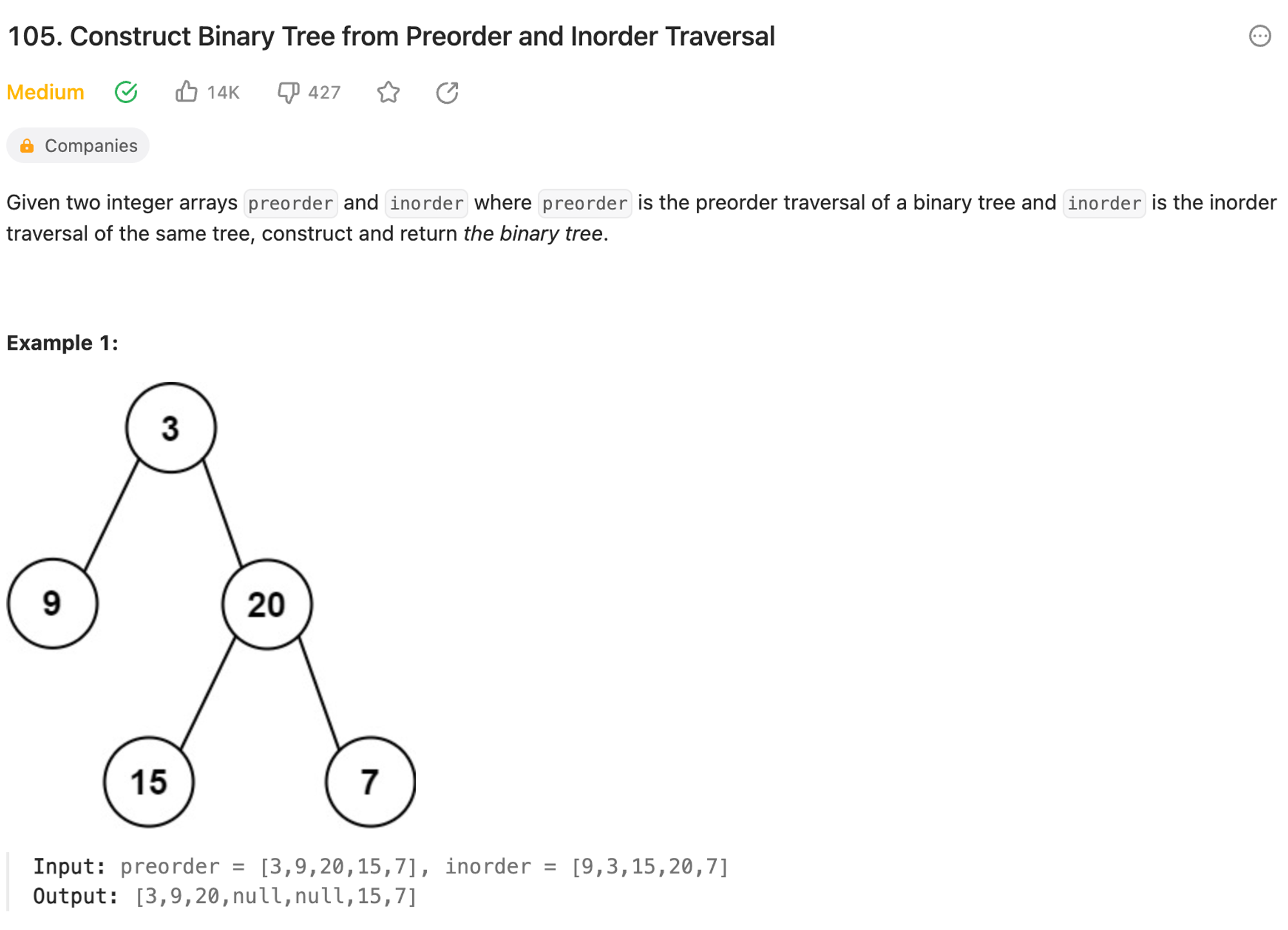
Problem

LeetCode - The World's Leading Online Programming Learning Platform

Solution

내 풀이

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:

        def dfs(pre_order, in_order):
            if not pre_order:
                return None

            mid = pre_order[0]
            mid_idx = in_order.index(mid)
            left_inorder = in_order[:mid_idx]
            right_inorder = in_order[mid_idx+1:]

            left_preorder = pre_order[1:len(left_inorder)+1]
            right_preorder = pre_order[len(left_inorder)+1:]

            left_node = dfs(left_preorder, left_inorder)
            right_node = dfs(right_preorder, right_inorder)

            return TreeNode(val=mid, left=left_node, right=right_node)

        return dfs(preorder, inorder)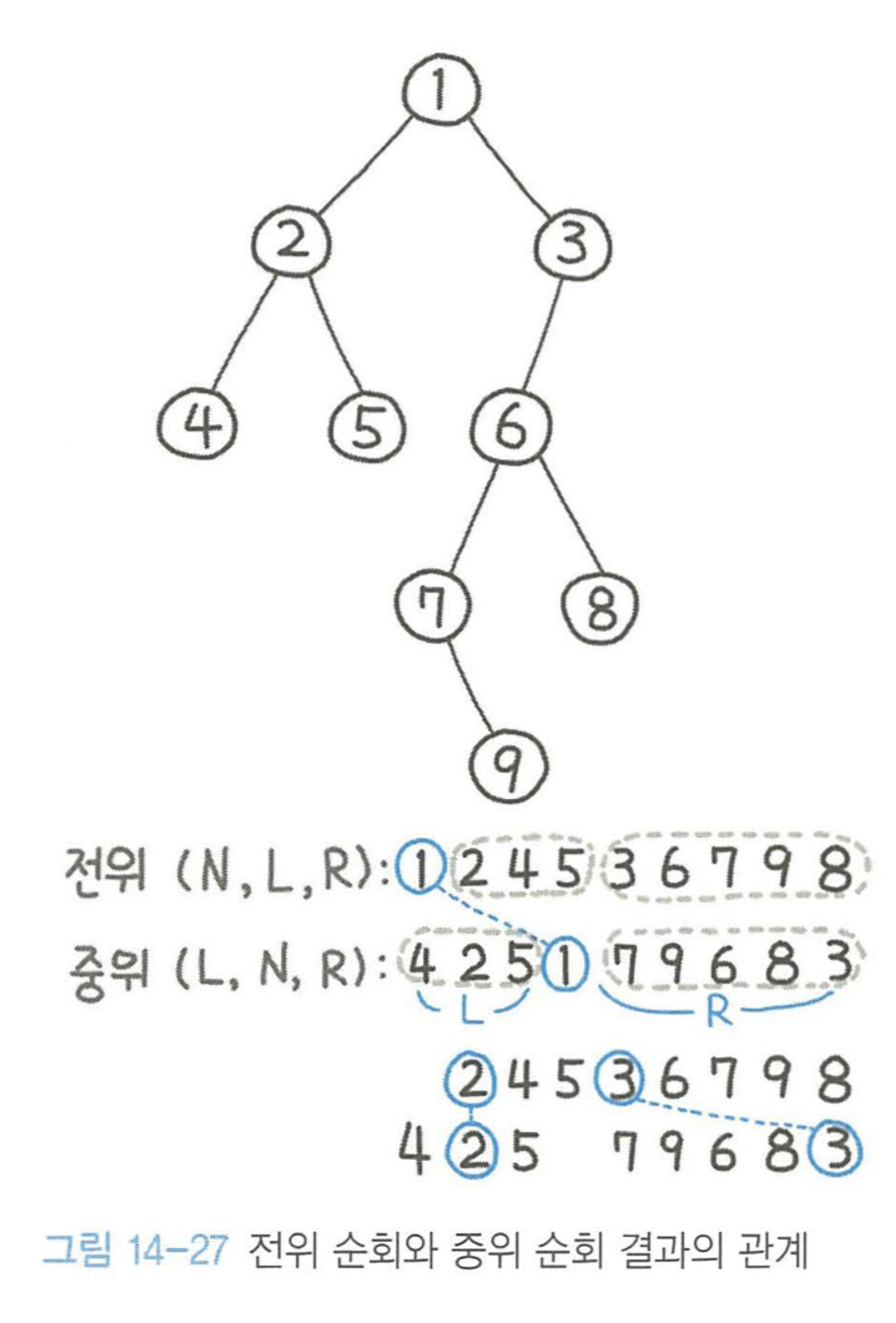     

책에 나와있는 전위 순회와 중위 순회의 관계를 보고 구현을 하였다.

전위 순회의 첫 원소가 중간 노드 임을 이용하여 문제를 풀었다.

다른 풀이

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if inorder:
            index = inorder.index(preorder.pop(0))
            
            node = TreeNode(inorder[index])
            node.left = self.buildTree(preorder, inorder[0:index])
            node.right = self.buildTree(preorder, inorder[index+1:])
            
            return node

책에 나와있는 풀이이다.

왼쪽으로 모든 탐색을 끝내고 오른쪽으로 넘어가기 때문에 preorder를 따로 가공하지 않고 pop(1)만 해줘도 된다. pop(1)이 O(n)이기는 하지만 preorder를 슬라이싱해서 재할당하는 시간이 없어지므로 시간 뿐만 아니라 공간 활용도 측면에서도 더 좋다.

Reference

파이썬 알고리즘 인터뷰 54번