[BOJ] 알고리즘 수업- 병합 정렬 1 (NodeJS) / 문제 풀이 및 해석

ChoiYongHyeun·2024년 5월 27일
자료구조와 알고리즘
0

알고리즘 이론

목록 보기
9/9
post-thumbnail

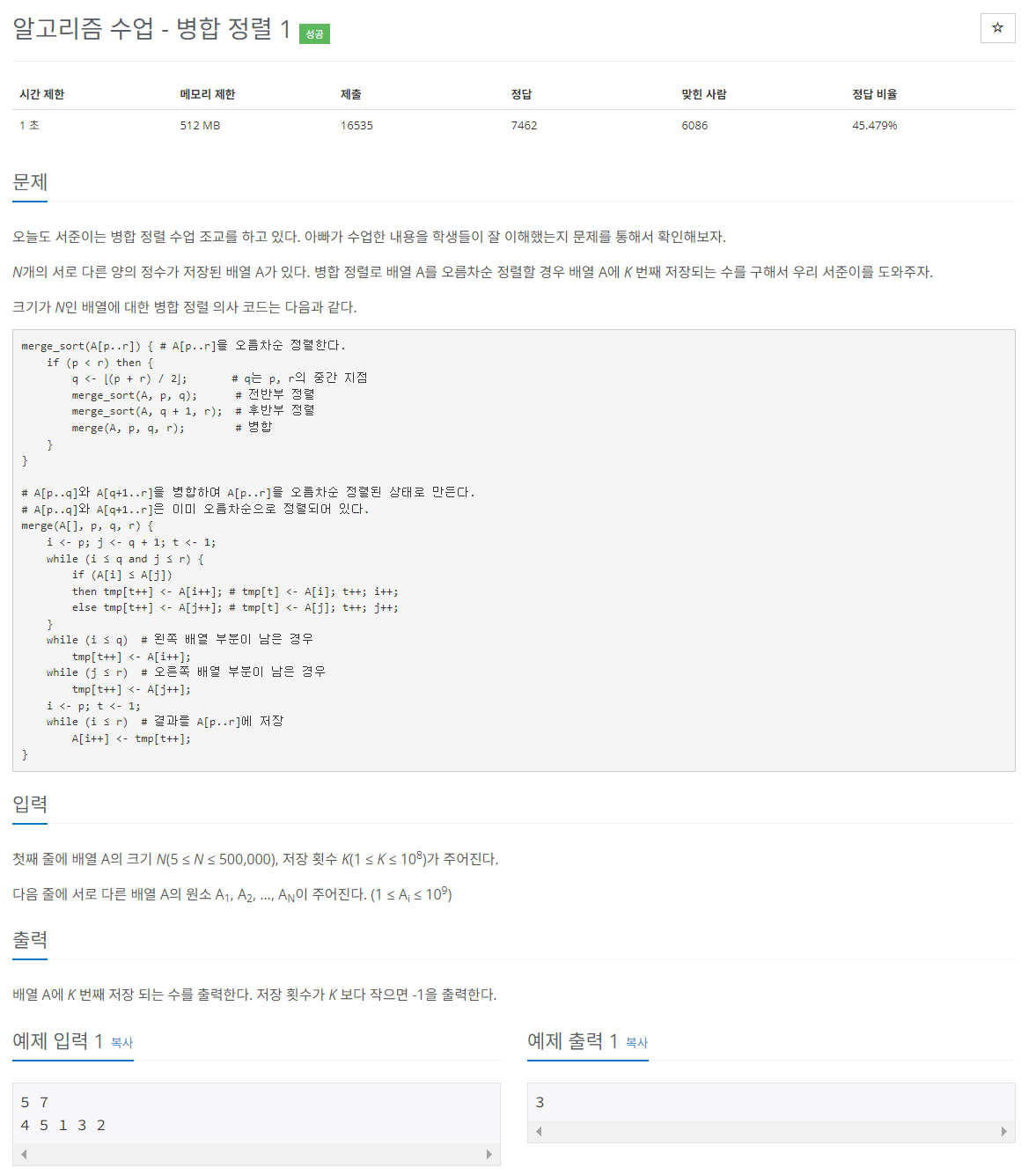
https://www.acmicpc.net/problem/24060

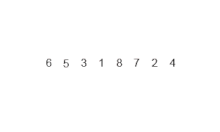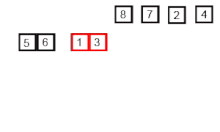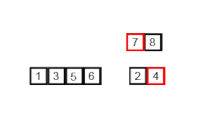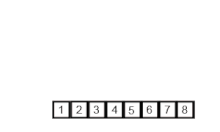
아이디어

사실 아이디어라 할 것도 없이 분할 정복 알고리즘을 주어진 슈도코드를 본인의 언어로 구현하는 문제였다.

분할 정복의 개념은 위키백과와 유튜브를 통해 이해했지만 이것을 코드로 쓰는 것이 어려웠다.

이미 누군가가 세워둔 코드를 참고하여 만들어도 재귀함수를 직관적으로 이해하기엔 아직 알고리즘적 사고가 부족한듯 싶었다.

그래도 코드의 흐름을 살펴보며 분할 정복 정렬의 과정을 살펴보자

코드

const fs = require('fs');
const filePath =
process.platform === 'linux' ? '/dev/stdin' : \_\_dirname + '/input.txt';
let inputs = fs.readFileSync(filePath).toString().split('\n');
const [N, K] = inputs[0].split(' ').map(Number);
let GlobalArr = inputs[1].split(' ').map(Number);

let cnt = 0;
let answer = -1;
function solution() {
function mergeSort(arr, start, end) {
// endPoint
if (start >= end) {
return;
}

    const mid = Math.floor((start + end) / 2);
    mergeSort(arr, start, mid); // mid 기준 좌측 배열 정렬 후 탈출
    mergeSort(arr, mid + 1, end); // mid 기준 우측 배열 정렬 후 탈출
    merge(arr, start, mid, end); // 호출 마다 mid 기준 좌측, 우측 배열 이용하여 정렬

}

function merge(arr, start, mid, end) {
const leftArr = arr.slice(start, mid + 1);
const leftLength = mid + 1 - start;

    const rightArr = arr.slice(mid + 1, end + 1);
    const rightLenght = end - mid;

    let leftPointer = 0;
    let rightPointer = 0;
    let GlobalPointer = start;

    // console.log('------');
    // console.log(`정렬 전 : ${GlobalArr}`);

    while (leftPointer < leftLength && rightPointer < rightLenght) {
      if (leftArr[leftPointer] <= rightArr[rightPointer]) {
        arr[GlobalPointer++] = leftArr[leftPointer++];
      } else {
        arr[GlobalPointer++] = rightArr[rightPointer++];
      }
      cnt++;
      if (cnt === K) answer = arr[GlobalPointer - 1];
    }

    while (leftPointer < leftLength) {
      arr[GlobalPointer++] = leftArr[leftPointer++];
      cnt++;
      if (cnt === K) answer = arr[GlobalPointer - 1];
    }

    while (rightPointer < rightLenght) {
      arr[GlobalPointer++] = rightArr[rightPointer++];
      cnt++;
      if (cnt === K) answer = arr[GlobalPointer - 1];
    }

    // console.log(`왼쪽 배열 : ${leftArr}`);
    // console.log(`오른쪽 배열 : ${rightArr}`);
    // console.log(`정렬 후 : ${GlobalArr}`);

}

mergeSort(GlobalArr, 0, N - 1);
// console.log('------');
// console.log(GlobalArr);
console.log(answer);
}

solution();

문제에서 요구하는 사항은 K 번 째 변경된 수를 찾는 것이기 때문에 그런 로직이 들어가긴 했으나 해당 부분은 무시하고 분할 정복 알고리즘의 과정에 중점을 두고 코드를 생각해보자

분할정복의 주 아이디어

분할 정복의 주 아이디어는 다음과 같다.

정렬되지 않은 배열을 정렬된 상태의 배열까지 분할 하고 정렬된 상태의 배열들을 이용해 정렬된 배열을 생성하는 정복 과정을 거친다.

분할 정복 정렬의 주요한 개념을 순서에 따라 살펴보자

1. 이미 정렬된 두 배열을 이용하여 정렬된 하나의 배열을 만들 수 있다. (정복)

이 단계는 정복 단계이다.

좌,우 배열의 값을 가리키는 좌,우 포인터들을 이용해 포인터가 가리키는 값의 대소 관계를 비교하고

대소 관계에 따라 전체 배열의 값을 가리키는 포인터에 조건에 맞는 값을 할당한다.

이 때 좌, 우 대소관계 비교 후 값이 더 작은 배열의 값이 할당 되었다면 더 작았던 값을 가리키던 포인터를 1 증가 시키고 , 다음 할당 될 전체 포인터의 값의 포인터도 1증가 시킨다.

만약 [2,4] , [1,3] 과 같이 정렬된 상태의 두 배열과 두 배열을 합친 [2,4,1,3] 배열이 존재한다면 다음과 같은 상황이 연출된다.

  1. [2,4] , [1,3] 중 좌 0 , 우 0 번째 포인터간 비교 => 우 0번째 포인터가 가리키는 값이 더 작으니 전체 0번째 포인터가 가리키는 0번째 값에 우 0 번째 포인터가 가리키는 값을 넣고 우 포인터, 전체 포인터 ++

전체 배열 : [1,4,1,3]

  1. [2,4] , [1,3] 중 좌 0 , 우 1번째 포인터간 비교 => 좌 0번째 포인터가 가리키는 값이 더 작으니 전체 1번째 포인터가 가리키는 1번재 값에 좌 0번째 포인터가 가리키는 값을 넣고 좌 포인터 , 전체 포인터 ++

전체 배열 : [1,2,1,3]

  1. [2,4] , [1,3] 중 좌 1, 우 1번째 포인터간 비교 => 우 1번째 포인터가 가리키는 값이 더 작으니 전체 2번째 포인터가 가맄키는 2번째 값에 우 1번째 포인터가 가리키는 값을 넣고 우 포인터 , 전체 포인터 ++

전체 배열 : [1,2,3,3]

  1. 우측 배열의 포인터가 모두 끝났기 때문에 대쇼 관계가 불가능하지만 , 좌 포인터가 좌 배열의 길이보다 작기 때문에 좌 포인터가 좌 배열의 길이에 도달 할 때 까지 좌 포인터가 가리키는 값을 전체 포인터가 가리키는 값에 할당 , 좌 포인터, 전체 포인터 ++

전체 배열 : [1,2,3,4]

이렇게 최초 [2,4,1,3] 과 같이 길이가 N 인 배열을 정렬된 배열 두 개로 나누고 대소 관계를 비교하여 정렬한다면 N 번의 비교만에 정렬된 배열을 생성 할 수 있다.

이 단계를 코드로 표현한 것이 위 코드의 merge 부분이다.

function merge(arr, start, mid, end) {
  /* arr 를 mid 기준으로 나눈 leftArr , rightArr 생성 */
  const leftArr = arr.slice(start, mid + 1);
  const leftLength = mid + 1 - start;

  const rightArr = arr.slice(mid + 1, end + 1);
  const rightLenght = end - mid;

  let leftPointer = 0;
  let rightPointer = 0;
  let GlobalPointer = start;

  while (leftPointer < leftLength && rightPointer < rightLenght) {
    /* 두 배열의 포인터가 종료 될 때 까지 대소 관계 비교 */
    if (leftArr[leftPointer] <= rightArr[rightPointer]) {
      arr[GlobalPointer++] = leftArr[leftPointer++];
    } else {
      arr[GlobalPointer++] = rightArr[rightPointer++];
    }
    cnt++;
    if (cnt === K) answer = arr[GlobalPointer - 1];
  }

  while (leftPointer < leftLength) {
    /* 만약 좌측 포인터가 끝까지 도달하지 못했을 때 좌측 배열의 값 할당하기 */
    arr[GlobalPointer++] = leftArr[leftPointer++];
    cnt++;
    if (cnt === K) answer = arr[GlobalPointer - 1];
  }

  while (rightPointer < rightLenght) {
    /* 사실 이 단계는 필요하지 않다. */
    arr[GlobalPointer++] = rightArr[rightPointer++];
    cnt++;
    if (cnt === K) answer = arr[GlobalPointer - 1];
  }
}

전체 포인터인 GlobalPointer 는 leftPointer 와 같이 시작하게 되는데 arr 의 시작 부분이 leftArr 의 시작 부분과 동일하기 때문이다.

while (rightPointer < rightLenght) {
  /* 사실 이 단계는 필요하지 않다. */
  arr[GlobalPointer++] = rightArr[rightPointer++];
  cnt++;
  if (cnt === K) answer = arr[GlobalPointer - 1];
}

마지막에 rightPointer < rightLength 단계에 주석으로 이 단계가 필요하지 않다고 설명했는데

만약 rightPointer 가 끝까지 도달하지 못하고 위의 while 문이 모두 끝나버렸다면 이미 arr 에 남은 부분들엔 rightArr 의 값이 이미 할당 되어 있기 때문이다.

[1,2] , [3,4] 를 가지고 머리속으로 시뮬레이션 해보면 leftArr의 값은 이미 위 while 문에서 [1,2] 는 arr 의 0,1 번째 값에 이미 모두 들어가고 rightArr 의 값은 옮겨주지 않아도 [3,4] 는 이미 2,3 번째 값에 존재한다.

2. 정렬되지 않은 배열은 분할을 통해 정렬된 배열까지 분할 할 수 있다. (분할)

위에서 정렬된 배열들을 이용하면 정렬된 하나의 배열을 생성 할 수 있었다.

하지만 초기 정렬되지 않은 배열들은 위 정복 과정을 거칠 수 없다.

그렇기 때문에 배열이 정렬된 상태인 단계까지 분할하기 위한 과정이 분할 단계이다.

  • [2,4,1,3] 은 분명히 정렬되지 않은 상태이다.
  • 정렬된 상태까지 분할하기 위해 mid 를 기준으로 배열을 나눠주자
  • [2,4] , [1,3] 은 분명히 정렬되지 않은 상태이다.
  • 정렬된 상태까지 분할하기 위해 mid 를 기준으로 배열을 나눠주자
  • [2] , [4] , [1] , [3] 은 분명히 정렬된 상태이다.

이렇게 분할하는 단계가 위 코드의 mergeSort 부분이다.

function mergeSort(arr, start, end) {
  /* 분명히 정렬된 상태가 된다면 재귀문 탈출 */
  if (start >= end) {
    return;
  }

  const mid = Math.floor((start + end) / 2);
  mergeSort(arr, start, mid); // mid 기준 좌측 배열 정렬
  mergeSort(arr, mid + 1, end); // mid 기준 우측 배열 정렬
  merge(arr, start, mid, end);
}

mergeSort 부분을 보면 mid 부분을 기준으로 좌측 배열 mergeSort 우측 배열 mergeSort 를 시행하는 모습을 볼 수 있다.

function mergeSort(arr, start, end) {
  if (start >= end) {
    return;
  }
  const mid = Math.floor((start + end) / 2);
  mergeSort(arr, start, mid); // mid 기준 좌측 배열 정렬
  mergeSort(arr, mid + 1, end); // mid 기준 우측 배열 정렬
  merge(arr, start, mid, end);
}

만약 위 부분이 맨 처음 호출되었을 때, 그러니 정렬되지 않은 원 배열이 해당 부분을 만나면 어떤 일이 벌어지는지 로그를 찍어보자

사실 일일히 줄줄 설명해봤지만 예시를 보는 것이 훨씬 직관적으로 이해된다.

------
정렬 전 : 4,5,1,3,2
왼쪽 배열 : 4
오른쪽 배열 : 5
정렬 후 : 4,5,1,3,2
------
정렬 전 : 4,5,1,3,2
왼쪽 배열 : 4,5
오른쪽 배열 : 1
정렬 후 : 1,4,5,3,2
------
정렬 전 : 1,4,5,3,2
왼쪽 배열 : 3
오른쪽 배열 : 2
정렬 후 : 1,4,5,2,3
------
정렬 전 : 1,4,5,2,3
왼쪽 배열 : 1,4,5
오른쪽 배열 : 2,3
정렬 후 : 1,2,3,4,5
------

각 로그들은 merge 함수가 실행 될 때 마다 로깅 되는 텍스트이다.

첫 번재 merge 가 언제 호출되는지를 살펴보면 [4,5,1,3,2] 란 배열이 좌측 배열 기준으로 완전 분할 된 [4] , [5] 단계 까지 간 후 호출되고

그 이후 호출은 [4] , [5] 이전 단계인 [4,5,1] 에서 호출되는 모습을 볼 수 있다.

이렇게 전체 배열의 좌측이 모두 분할 , 정복 되고 나면 우측 배열이 차례로 분할, 정복이 일어난다.

좀 더 복잡한 예시로 살펴보자

------
정렬 전 : 8,10,3,9,4,5,1,7,2,10
왼쪽 배열 : 8
오른쪽 배열 : 10
정렬 후 : 8,10,3,9,4,5,1,7,2,10
------
정렬 전 : 8,10,3,9,4,5,1,7,2,10
왼쪽 배열 : 8,10
오른쪽 배열 : 3
정렬 후 : 3,8,10,9,4,5,1,7,2,10
------
정렬 전 : 3,8,10,9,4,5,1,7,2,10
왼쪽 배열 : 9
오른쪽 배열 : 4
정렬 후 : 3,8,10,4,9,5,1,7,2,10
------
정렬 전 : 3,8,10,4,9,5,1,7,2,10
왼쪽 배열 : 3,8,10
오른쪽 배열 : 4,9
정렬 후 : 3,4,8,9,10,5,1,7,2,10
------
정렬 전 : 3,4,8,9,10,5,1,7,2,10
왼쪽 배열 : 5
오른쪽 배열 : 1
정렬 후 : 3,4,8,9,10,1,5,7,2,10
------
정렬 전 : 3,4,8,9,10,1,5,7,2,10
왼쪽 배열 : 1,5
오른쪽 배열 : 7
정렬 후 : 3,4,8,9,10,1,5,7,2,10
------
정렬 전 : 3,4,8,9,10,1,5,7,2,10
왼쪽 배열 : 2
오른쪽 배열 : 10
정렬 후 : 3,4,8,9,10,1,5,7,2,10
------
정렬 전 : 3,4,8,9,10,1,5,7,2,10
왼쪽 배열 : 1,5,7
오른쪽 배열 : 2,10
정렬 후 : 3,4,8,9,10,1,2,5,7,10
------
정렬 전 : 3,4,8,9,10,1,2,5,7,10
왼쪽 배열 : 3,4,8,9,10
오른쪽 배열 : 1,2,5,7,10
정렬 후 : 1,2,3,4,5,7,8,9,10,10
------

좌측 배열인 [3,8,10,4,9] 를 기준으로 하여 다시 좌 우 분할 정복을 차례로 한 후

우측 배열을 토대로 좌 우 분할 정복을 하는 모습을 볼 수 있다.

결국 mergeSort 가 최초 호출된 시점 호출되어야 하는 merge 는 이미 정렬된 좌 우 배열을 토대로 merge 가 일어나게 된다.

시간 복잡도

분할 단계는 길이가 N 인 배열을 1/2 씩 줄여가며 일어나기 때문에 O(log N) 만큼의 시간 복잡도가 걸린다.

정복 단계는 길이가 N 인 배열을 모두 순회하며 할당하기 때문에 O(N) 만큼의 시간 복잡도가 걸린다.

profile
ChoiYongHyeun
빨리 가는 유일한 방법은 제대로 가는 것이다
이전 포스트

[Javascript] Heap 자료구조

0개의 댓글