이진 탐색 트리 - 정의와 탐색, 연산

ChoiYongHyeun·2023년 11월 30일

자료구조와 알고리즘

알고리즘 이론

목록 보기

7/9

이진 탐색 트리

정의

각 노드의 왼쪽 subtree 의 key 값은 노드의 key 값보다 작거나 같아야 한다.
오른쪽 subtree의 key 값은 노드의 key 값보다 커야 한다.

해당 조건을 모두 만족하면 이진 탐색 트리 (Binary Search Tree) 라고 한다.

장점

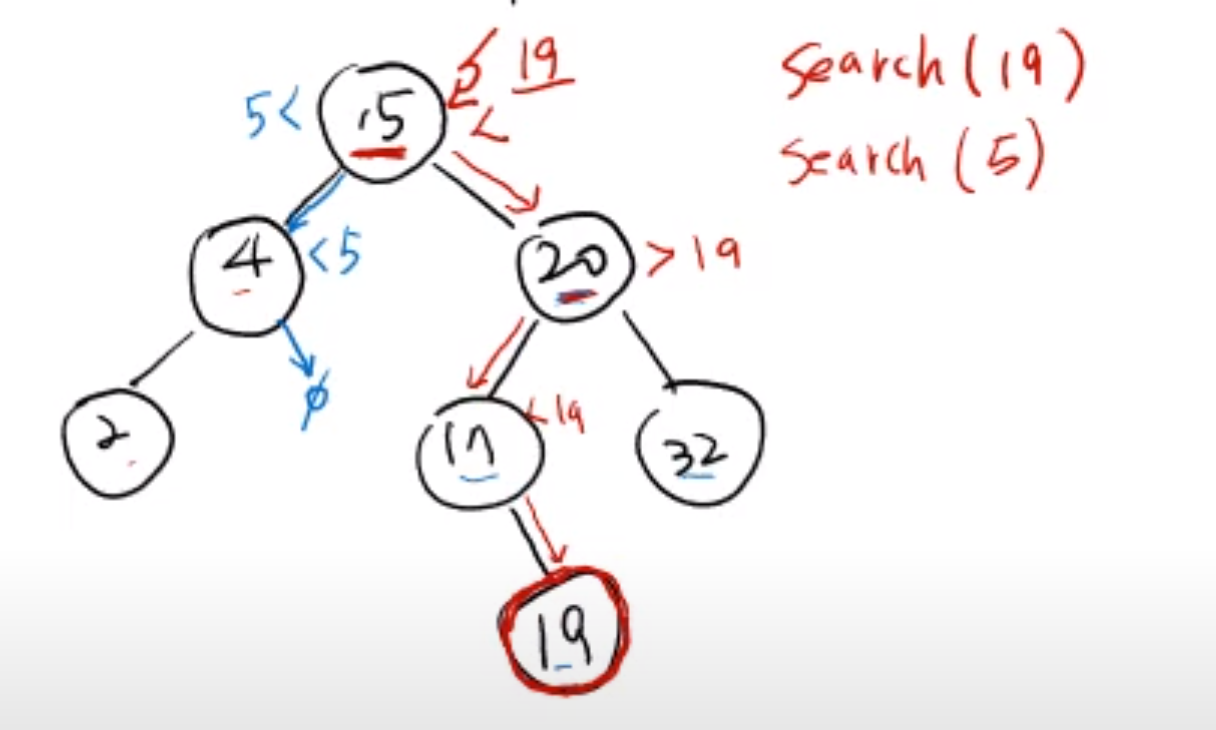
어떤 값을 찾고자 할 때 몇 번의 비교 연산을 통해서 빠르게 해당 값이 존재하는지, 존재하지 않는지를 확인 할 수 있다.

기존 N 개의 배열에서 어떤 원소가 있는지를 확인하기 위해서는 $O(N)$ 의 시간이 필요했다면

이진 탐색 트리에서는 이진 탐색 트리의 높이를 $H$ 라고 한다면

$O(H)$ 밖에 걸리지 않는다.

탐색

class Node:

  def __init__(self,  key):
    self.key = key 
    self.parent = self.left = self.right = None

  def __str__(self):
    return str(self.key)
  
  def preorder(self):
    if self != None:
      print(self.key)
      if self.left:
        self.left.preorder()
      if self.right:
        self.right.preorder()

  def inorder(self):
    if self != None:
      if self.left:
        self.left.inorder()
      print(self.key)
      if self.right:
        self.right.inorder()

  def postorder(self):
    if self != None:
      if self.left:
        self.left.postorder()
      if self.right:
        self.right.postorder()
      print(self.key)

  
class BST:

  def __init__(self):
    self.root = None 
    self.size = 0

  def __len__(self):
    return self.size
  
  def __iter__(self):
    '''
    root node 는 Node 객체 
    Node 객체에 설정되어 있는 __iter__ 에 맞게 함수가 실행되도록 한다.
    '''
    return self.root.__iter__()
  
  def find_loc(self, key):
    '''
    key 값 node 가 있다면 해당 node 를 return
    없다면 해당 node 가 삽입 될 부모 node 를 return
    ''' 
    if self.size == 0:
      return None 
    
    p = None # 부모 노드
    v = self.root  # 자식 노드 

    while v != None: # 자식 노드가 none 이 아닐 때 까지 
      if v.key == key:
        return v 
      elif key <= v.key:
        p = v 
        v = v.left
      else:
        p = v 
        v = v.right

    return p 
  
  def search(self,key):
    v = self.find_loc(key)
    if v == None:
      return None
    else:
      return v 

  def insert(self,key):
    p = self.find_loc(key)
    
    if p == None or p.key != key:
      v = Node(key)
      if p == None:
        self.root = v
      else:
        if v.key <= p.key:
          p.left = v 
        else:
          p.right = v
        v.parent = p 
      self.size += 1
    else:
      print('key is already in trees')
      return p

우선 BST 클래스를 생성해주고 BST 클래스는 Node 클래스들이 부모, 좌측 자식 , 우측 자식 링크를 갖는 객체들을 연결해준다.

맨 첫 BST의 생성자로는 가장 맨 위에 존재해야 하는 root node , 좌측 우측 자식 노드인 left , right node 들이 모두 None인 상태로 존재한다.

어떤 key 값이 BST 내부에 존재하는지를 확인하는 find_loc 함수를 뜯어보자

  def find_loc(self, key):
    '''
    key 값 node 가 있다면 해당 node 를 return
    없다면 해당 node 가 삽입 될 부모 node 를 return
    ''' 
    if self.size == 0:
      return None 
    
    p = None # 부모 노드
    v = self.root  # 자식 노드 

    while v != None: # 자식 노드가 none 이 아닐 때 까지 
      if v.key == key:
        return v 
      elif key <= v.key:
        p = v 
        v = v.left
      else:
        p = v 
        v = v.right

    return p

만약 self.size == 0 이라면 root node 가 None 이란 것이니 너가 찾는 것이 없다며 None 을 return 해주자

만약 BST 가 존재 할 경우 부모 노드와 자식 노드의 값을 변경해가며 찾아가면 된다.

반복문은 가장 마지막 left node 에 도달 할 할 때 까지 반복한다.

만약 밑으로 순회하면서 key 값과 같은 자식 노드를 발견한다면 해당 노드를 return 하면 된다.

만약 못찾았다면 반복적으로 찾아가는데

내가 찾고자 하는 값이 부모 노드의 값보다 작다면 , 부모 노드의 왼쪽 서브 트리에 존재하니 왼쪽 서브트리로 접근한다.

접근하는 과정에서 현재 부모 노드와 자식 노드의 값이 변경된다.

반대의 경우도 같다.

그렇게 반복문이 반복되면서 가장 밑 leaf node 까지 도달하던 도중 key 값을 가진 노드를 발견한다면 v 를 return 하면서 반복문이 종료 될 것이고

만약 반복문이 모두 끝났는데도 key 값을 가진 node를 찾지 못했다면

부모 노드 를 return 해준다.

왜?

find_loc 는 search , insert 하기 위한 부분 함수이다.
어차피 어떤 값이 반복문 중에 찾았다면 해당 값을 return 하게 된다.
부모 노드를 리턴하는 경우는 BST 내에 해당 key 값을 가진 노드가 존재하지 않는다는 뜻
만약 어떤 key 값을 insert 하려고 할 때에는 return 받은 부모 노드의 값을 가지고 결과에 따라 값을 삽입하기 위함이다.

삽입

  def insert(self,key):
    p = self.find_loc(key)
    
    if p == None or p.key != key:
      v = Node(key)
      if p == None:
        self.root = v
      else:
        if v.key <= p.key:
          p.left = v 
        else:
          p.right = v
        v.parent = p 
      self.size += 1
    else:
      print('key is already in trees')
      return p