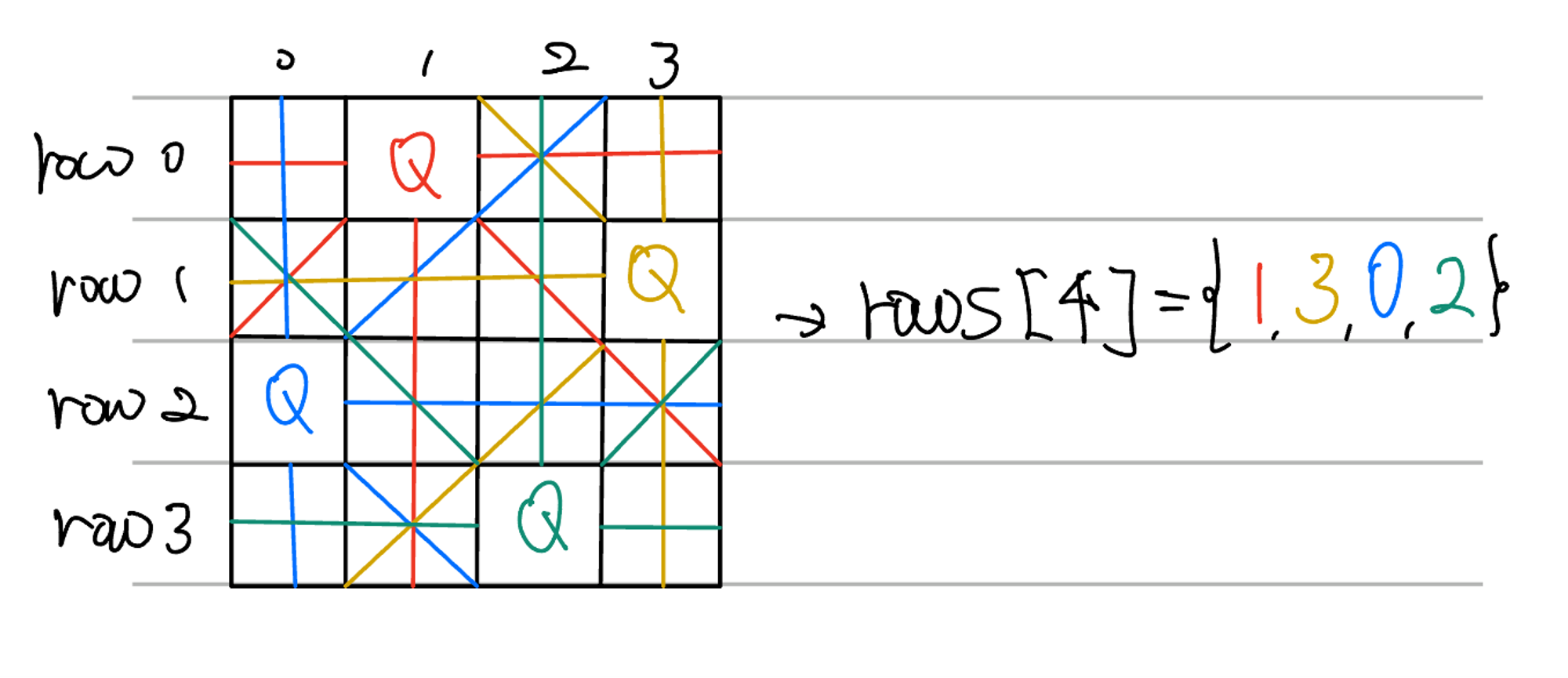
시도
처음엔 체스도 할 줄 몰라 퀸이 어떻게 놓이는지도 몰랐다.
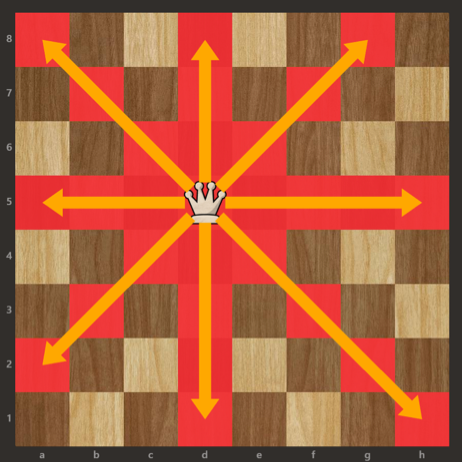 사진 출처
사진 출처
당연히 N*N맵을 만들어 구현하였다.
개같이 머리폭발
풀이를 찾아보았고, 2차원이 아닌 1차원으로 탐색을 하는 방식이 가능하다는 것을 알게 되었다.
문제의 핵심
퀸은 내 위치를 포함한 주변 8칸, 직선거리, 대각선 거리를 모두 움직일 수 있다.
한 퀸은 다른 퀸이 움직일 수 있는 위치 내에 위치하면 안된다.
즉, 한 행, 또는 한 열이 겹치지 않도록 퀸은 하나만 존재 가능하다는 것이다.
이 성질을 활용하여 행 단위, 또는 열 단위로 퀸이 어디에 존재하는 가를 저장하는 식으로 1차원 배열만을 활용하여 구현을 할 수 있다.
해설

- 한 행(row)마다 퀸이 하나 씩만 존재가능하니 행 단위로 퀸의 위치를 인덱스로 표현하는 배열을 활용한다.
- row 0에서 퀸은 1번째 열에 존재하니
row[0] = 1 - row 1에서 퀸은 3번째 열에 존재하니
row[1] = 3 - n-1번째 row 까지... 와 같은 방식이다.
위와 같이 구현하면 백트래킹도 편리하다.
한 번 트리구조의 백트래킹을 통해 살펴보자.
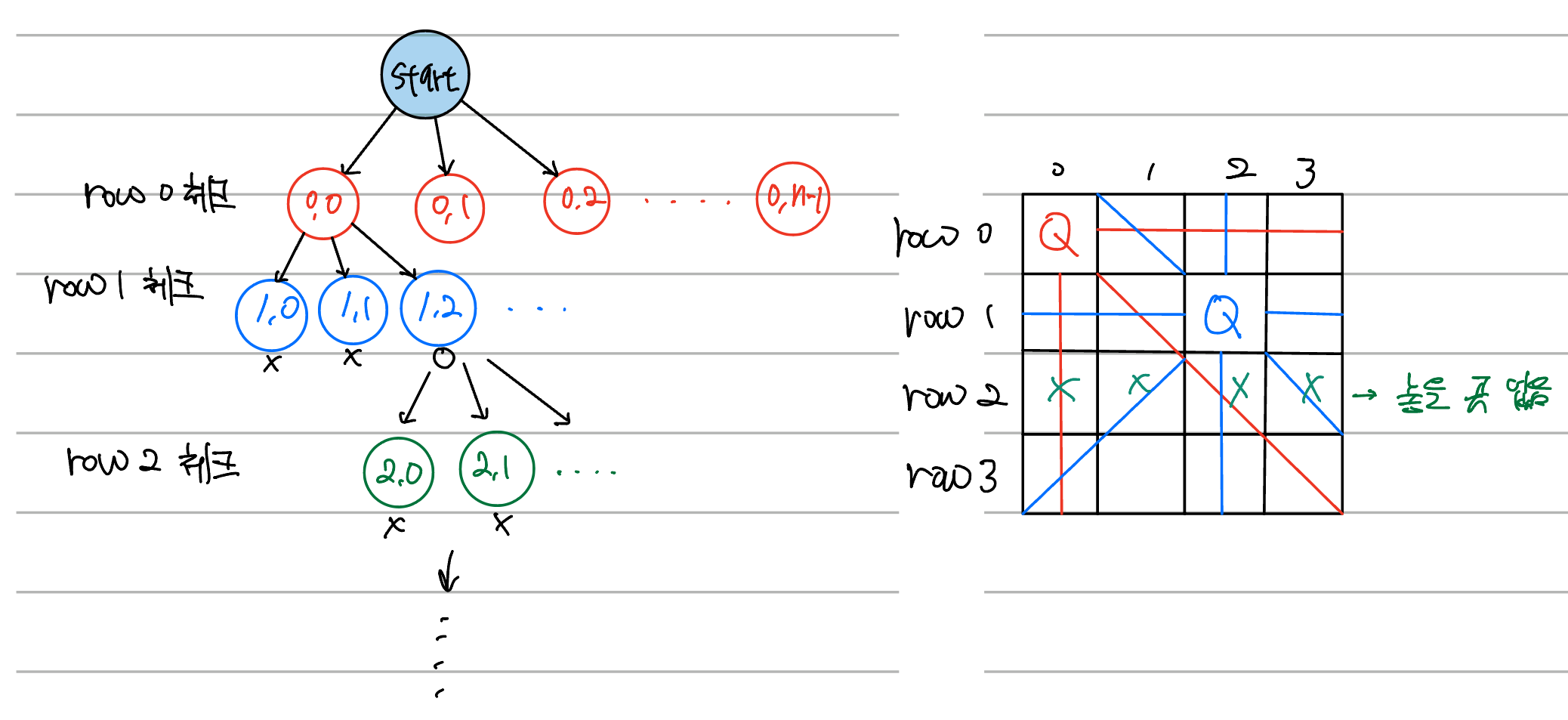
위와 같은 방식이다.
한 행씩 체크해 가며 놓을 수 있는 곳을 확인하고 해당 n번째 행의 m번째 열 (n,m)에 놓을 수 있다면 가지를 뻗어 다음 행을 체크하는 방식이다.'
가지치기 조건
그럼 가지를 뻗으면 안되는, 가지치기를 하면 안되는 경우의 수에 대해서 살펴보자.
크게 2가지의 조건을 검사해야 한다.
- 행 단위로 1개의 퀸만 저장하므로 (
rows[n]배열 활용) 같은 행에서 2개 이상의 퀸이 존재할 경우의 수는 고려하지 않아도 해결된다. - 같은 열에 퀸이 놓이는 경우의 수
rows[before] - rows[current] == 0(즉, 두 값이 같은 경우)
(current는 현재 놓일 퀸의 행 위치, before는 이전에 놓여져 있는 퀸들의 행 위치이다.)
ex)rows[before]는 n번째 열에 위치하고,rows[current]는 n번째 열에 위치한다.
즉, 두 값은 같게 된다. - 같은 대각선 상에 퀸이 놓이는 경우의 수
abs(rows[before] - rows[current]) == abs(before - current)
ex)rows[0]은 1번째 열에 위치하고,rows[2]는 3번째 열에 위치한다.
즉,abs(1-3) == abs(0-2)->2==2
위 2가지 조건 중 하나라도 부합하는 before가 한 개라도 존재한다면 current 위치에 퀸을 놓는 것이 불가능하다.
구현
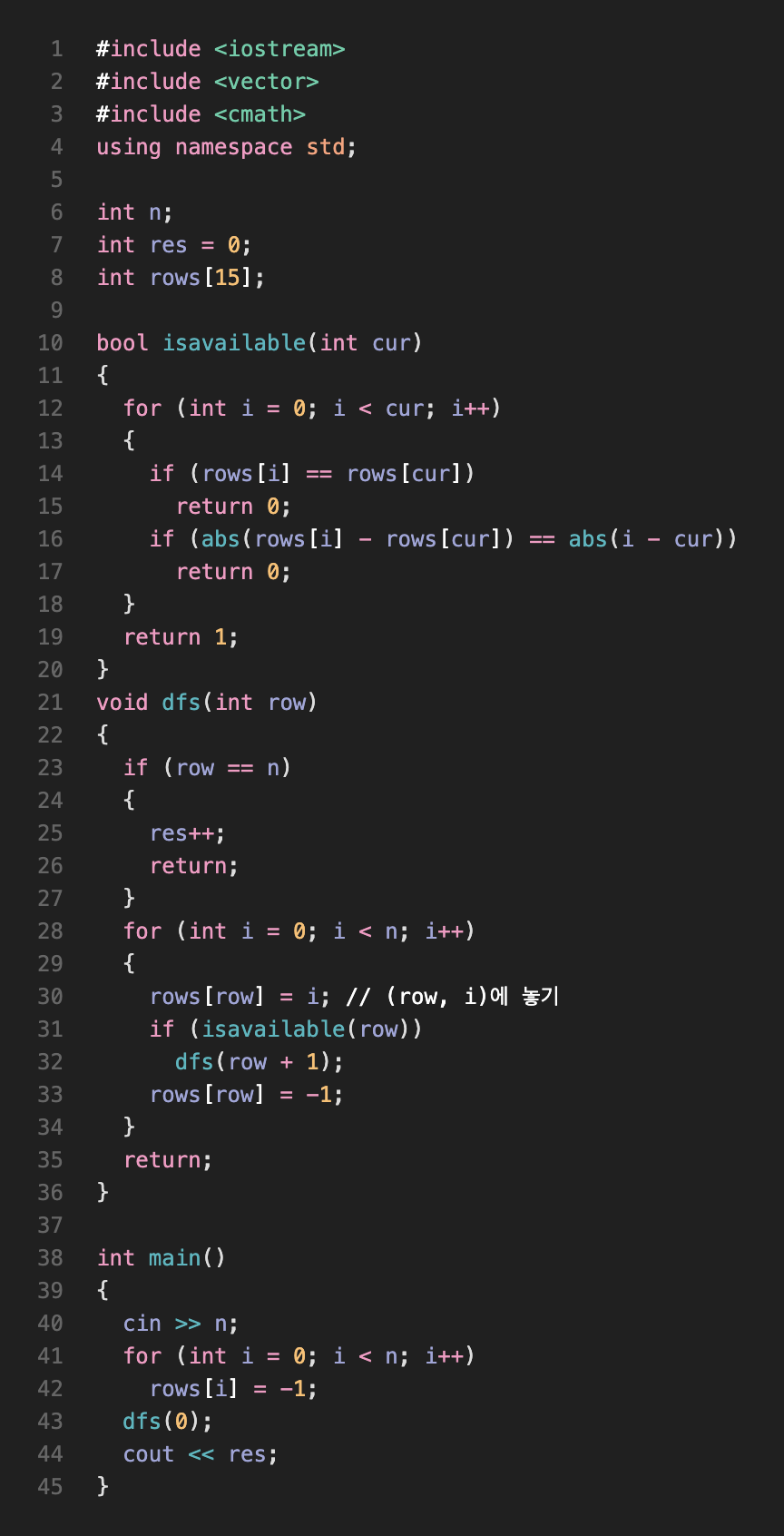
후기
- 백트래킹에 더 익숙해져야 하는 것을 알게 되었다.
- 백트래킹의 개념은 쉽지만 이를 직접적으로 구현해 내는 것은 아직 어려운 것 같다.
- 해당 문제에서 2차원 배열이 아닌 1차원 배열으로만도 문제를 해결할 수 있다는 것을 알게 되었다.
- 효율적인 자료구조 제작에 고민을 많이 해봐야겠다...
