[백준] 1043.거짓말(C++)

1043.거짓말

시도

전형적인 그래프 문제이다.

나는 플로이드워셜로 구현을 했고,
Union&Find를 활용해서도 해결 할 수 있어 두 가지 방법으로 문제를 풀어봤다.
사실 N의 값이 50이라 어떻게 풀어도 문제가 없을 듯하다.

해설

1. 한 파티에 진실을 아는 사람(t1)이 존재한다. → 해당 파티 참여 불가능
2. 다른 파티를 확인해보자. 해당 파티에 t1이 없어도 t1이 있는 파티에 있던 사람(t2)이 존재한다면 이 파티 또한 참여 불가능하다.
3. 거짓말은 진실을 아는사람을 통해 연쇄적으로 계속 작용하여 진실을 몰랐던 다른 사람 t3, t4, t5 ...에게도 퍼져 나간다.

진실을 아는 사람, 그와 같이 있던 사람, 그리고 그 사람과 같이 있던 사람, 그리고 또 그 사람과 같이 있던 사람...

그래프로 보면 노드하나를 기준으로 그 노드와 이어진 모든 노드를 발견하면 된다.

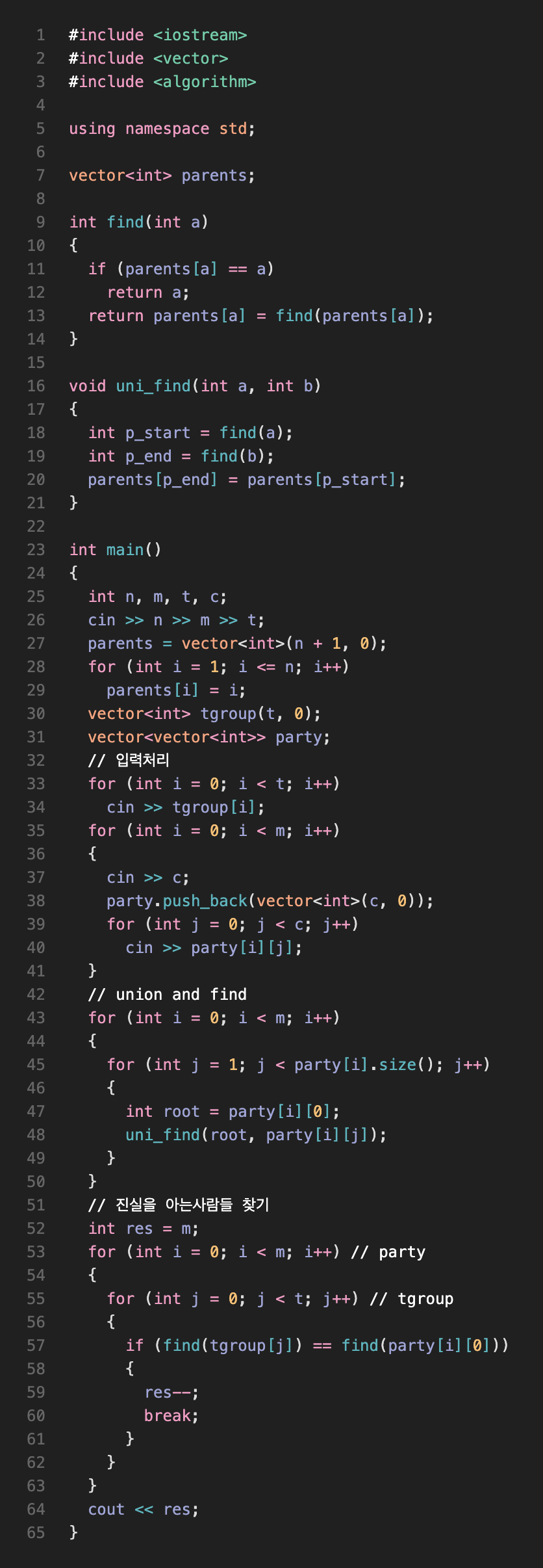
구현

Floyd Warshall

1. 모든 노드의 최단거리를 구할 수 있는 플로이드-워셜 알고리즘을 활용하여 최단거리를 갱신하고, 그 이후에도 최단거리가 INF 값이면 해당 노드에 도달할 수 없다는 뜻이다.
2. Adjacent Graph에서 최초 진실을 아는 그룹(tgroup)과, 그와 연결되어있는 노드들을 모두 해쉬맵인 knows_true의 값을 true로 설정한다.
3. 모든 파티를 탐색하여 해당 파티에 true값을 가진 노드가 하나라도 존재하면 해당 파티는 참여 불가능하며, 탐색을 멈추고 다음 파티를 탐색한다.

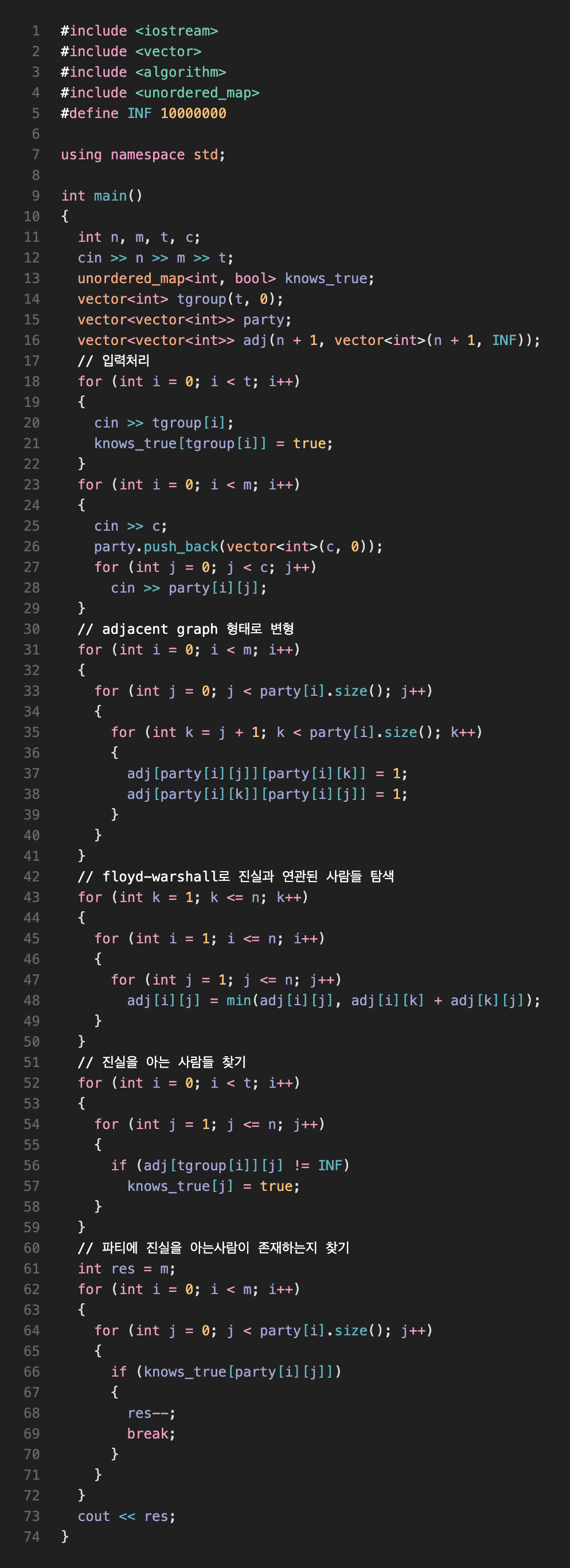
Union&Find

1. 모든 파티를 탐색하며 같은 파티에 존재하는 사람들끼리 한 그룹으로 만들어준다.
   1-1. 그룹의 대표 노드를 파티의 0번째 사람으로 임의로 설정하고 0번째 사람과 나머지 파티인원을 union해준다.
   1-2. 해당 수행을 하다보면 여러 파티에 속한 인원들도 있을 것이고, 진실을 아는 사람도 있을 것이다. union을 통해 자동으로 같은 집합에 속하게 된다.
2. 다시 모든 파티를 탐색한다. 한 파티의 대표자를 0번째 노드로 임의로 설정하고 해당 노드의 find값과, tgroup의 한 노드의 find값이 같다면 해당 파티는 참여 불가능하며, 탐색을 멈추고 다음 파티를 탐색한다.