시도
RGB거리 문제의 심화버전이다.
이웃한 집의 색이 달라야한다는 조건에 추가적으로 첫번째 집과 마지막 번째 집의 색깔 또한 달라야한다는 조건이 추가되었다.
사실... 너무 어렵게 접근을 시작했다.
그래도 내가 접근했던 방식을 설명하고자 한다.
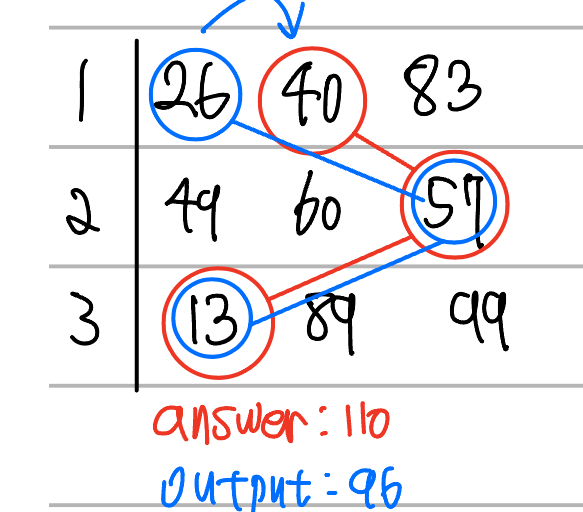
위와 같이 마지막 집과 첫번째 집의 색깔이 같을 경우만 거르면 되기 때문에
- 최소비용을 구하는 dp배열,
- 첫번째 집이 무슨 색을 칠했는지 저장하는 color1 배열,
- 그리고 그 첫번째 집과 마지막 집의 색이 겹친다면 첫번째 집의 색깔을 바꿔야하기 때문에 두번째 집과 색이 겹치지 않기 위해 두번째 집의 색을 저장하는 color2 배열
을 만들어 조건부로 문제를 풀어봤다...
찾을 수 있는 반례는 다 통과했지만 아무리 해도 틀렸습니다를 이겨낼 수 없었기에...
결국 다시 접근하여 문제를 풀었다.
해설
그냥 위에서 했던 뻘짓을 정리하면 아주 간단하다.
dp[n][3] 현재 n번째 집이 R(0), G(1), B(2)일 때 최소비용의 합이다.
- 현재 색이 R일때, 이전 집이 G, B를 칠했을 경우 중 최소비용 + R의 비용
- 현재 색이 G일때, 이전 집이 R, B를 칠했을 경우 중 최소비용 + G의 비용
- 현재 색이 B일때, 이전 집이 R, G를 칠했을 경우 중 최소비용 + B의 비용
와 같이 점화식을 세울 수 있는데 여기까지는 동일하고,
첫번째 집의 선택에 제약을 걸어주기만 하면 된다.
만약,dp[n][0] (n번째 집에 R을 칠했을 때의 최소비용)을 구하려면
dp[0][0] (첫번째 집을 R로 칠했을때) 값을 INF로 설정해 주는 것이다.
그러면 R로 시작하지 않는 것이 보장된다.
위 수행을 R, G, B에 대해서 한 번씩 수행하고 그때 나오는dp[n][0],dp[n][1],dp[n][2] 값을 저장하여 그 중 최소값이 전체 최소비용이 된다.
구현
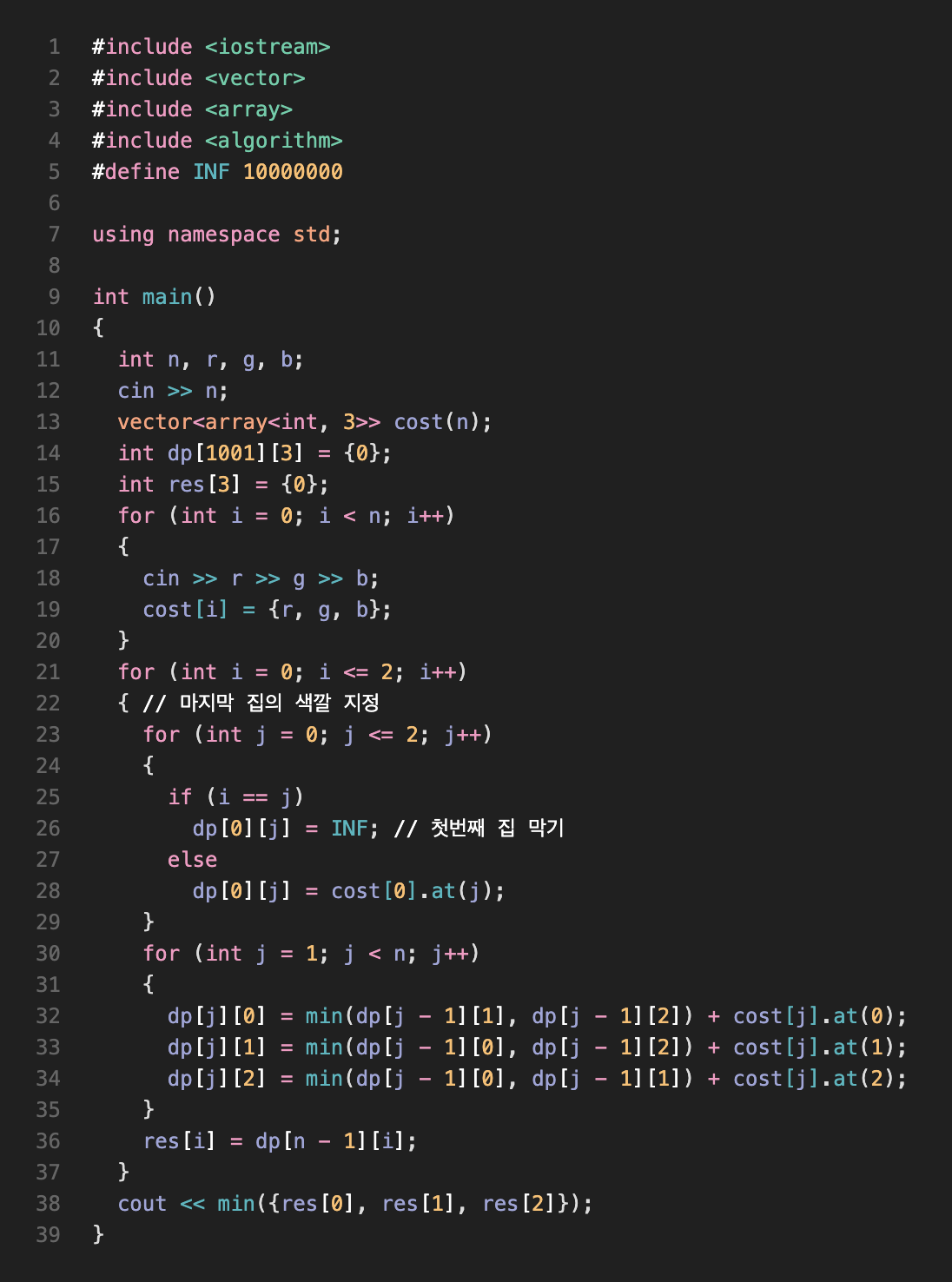
후기
DP에서의 제약조건을 걸 때 그래프 탐색과 같이 INF를 설정하는 테크닉을 배웠다.
DP가 익숙해질 때까지 노력하자...
그리고 C++ array 자료구조를 처음 사용해봤다.
(사실 있는지도 몰랐는데)
array<타입, 크기>와 같이 선언하여 접근시 .at(인덱스)를 통해 참조가 가능한데,
해당 자료구조를 사용했던 이유가 튜플에서의 인덱스 접근 시 변수 사용이 불가능해서 였다.
tuple 자료형에서 참조 시 get<변수>(튜플명)에서 <> template 자리에 변수가 안들어가졌다.
get<j>(cost[0]) -> cost[0].at(j) 로 바꿔서 사용해서 문제를 해결했다.
