The Small-World Problem(1967) - Stanley Milgram
문제 정의
- 우리는 이 세상에 있는 임의의 X와 Z가 서로 아는 사이인지의 문제를 풀고 싶다.
- 이 문제의 가장 기본적인 아이디어는 X와 Z라는 사람이 서로 모를 때 X는 Y를 통해 Z와 이어져있을 수 있다라는 것이다.
- 우리는 X와 Z가 아는가라는 질문에서 X와 Z가 몇 다리를 거치면 서로 알 수 있을까라는 질문으로 조금 수정해볼 수 있다.
문제에 대한 다양한 관점
철학적 관점
- 이에 대한 해답으로 큰 두가지 철학적인 관점이 존재했는데
- 하나는 아무리 멀리 떨어진 사람들이더라도 지인이라는 매개를 이용하여 서로에게 도달할 수 있다라는 것이었다.
- 나머지 하나는 임의의 두 사람에게는 연결할 수 없는 간극이 존재할 수도 있다고 한다. 그 근거는 사람들은 특정한 그룹을 형성하며 살고 또한 그룹 간의 도약은 쉽지 않기에 교차하지않는 그룹이 존재하여 서로 연결하기 힘들 것이다라는 거이다.
이론적인 관점
- 이 문제를 조금 더 일반화 해보았을 때 2억 개의(당시 미국 인구인 것 같음) vertices 중 2개를 임의로 선택하였을 때 그 2개의 최단 거리를 구하는 문제로 볼 수 있다.
- 당시 MIT에서의 조사에 따르면 한 사람 당 약 500명의 지인을 가지고 있다고 한다.
- 즉 2억개의 vertices와 각각의 vertex는 500개의 incident edges를 가지는 그래프를 만들 수 있다.
실험적인 관점
- 임의로 실험자를 선정하여 그 실험자들에게 어느 지역에 사는 특정 사람에게 편지를 보내라고 시킨다.
- 만약 그 사람을 모를 경우 그 사람을 가장 잘 알 것 같은 사람에게 보내어 끝내 전달되도록 한다.
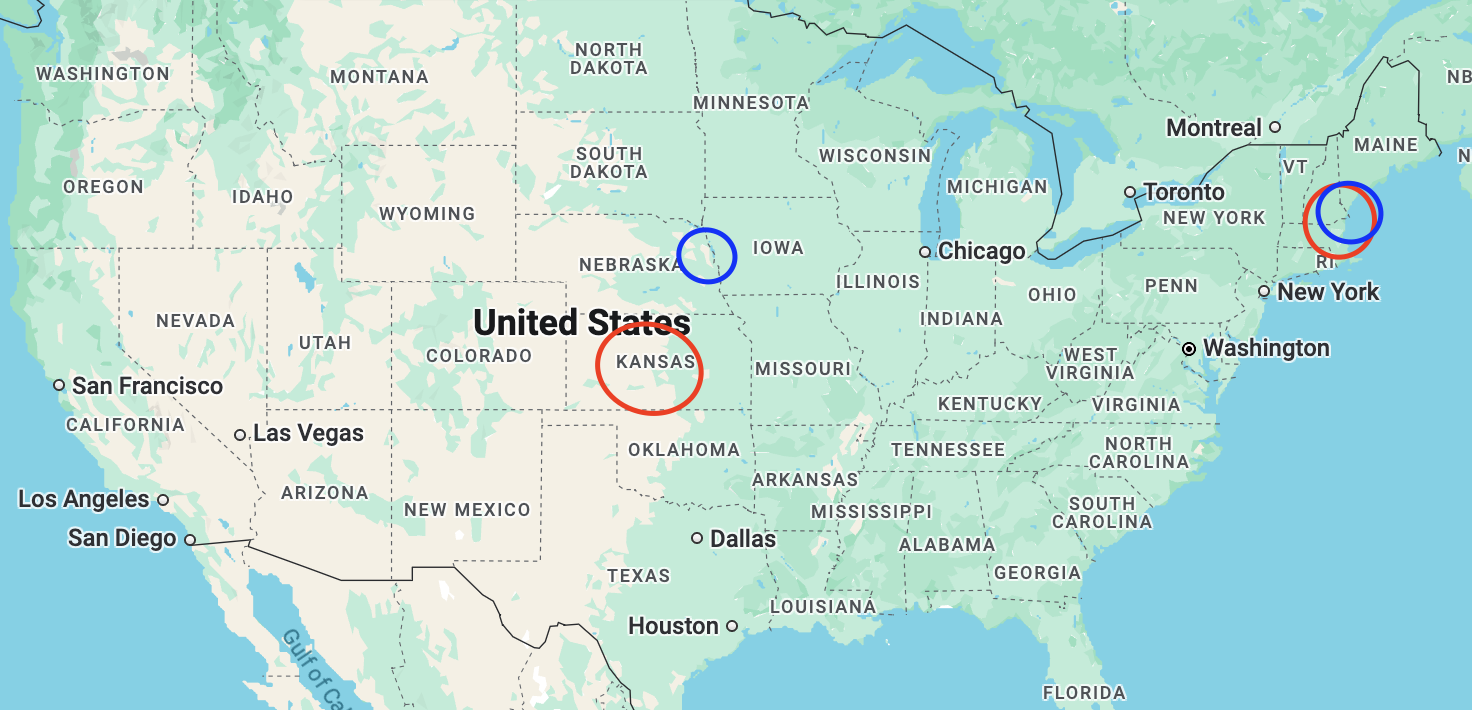
- 첫 실험에서는 Wichita, Kensas에서 시작하여 Cambridge에 사는 학생의 부인에게 전달되도록 하였다.
- 두번째 실험에서는 Omaha, Nebraska에서 시작하여 Boston에서 일하고 Sharon에 사는 증권 중개인에게 전달되도록 하였다.
- 실험의 첫번 째 사람은 문서가 든 폴더를 받는다.
- 문서에는 타깃사람의 이름과 정보를 가지고 있었다. 또한 실험에 대한 설명이 쓰여있었고 가장 중요한 지나온 사람들의 이름을 기록하는 공간이 있었다.
- 이 폴더를 타깃사람을 가장 잘 보낼 것 같은 사람에게 보내며 tracer card에 자신의 이름을 써서 보낸다.
실험 결과
- 2-10개의 중간다리를 거쳐 목표에 도착했고 약 5다리가 평균이었다.
실험의 긍정적인 관점
- 하지만 실제로는 이보다 더 적은 단계가 필요할 것이라고 한다.
- 사람들은 자신이 연락가능한 지인 중 해당 타깃을 알 것 같은 사람에게 연락을 돌리는데 때 항상 최선의 선택을 하는 것이 아니기에 그래프에서 최단 거리에 해당하지 않을 수 있다
- 그들은 문서에 있는 정보를 토대로 해당 타깃을 알 것 같은 사람을 추정하는데 이때 자신의 지인에 대한 정보를 완전히 알지 못하는 경우 판단에 있어 또한 제약을 받게 된다.
실험의 부정적인 관점
- 첫번째 실험은 160개로 시작했지만 오직 44개만 최종적으로 도달했고 126개는 도달하지 못하였다.
- 이는 10개의 다리보다 더 많이 걸리며 도달하는 길을 잃었을 가능성을 생각할 수 있다.
실험의 추가적인 통찰
- 왼쪽이 보내는 쪽이고 위쪽이 받는 쪽이라 하였을 때 같은 성별에게 전달하는 경향이 보였다.
남 여 남 58 13 여 18 56 - 123개가 친구나 지인에 의해 전달되었고 22개가 친족을 통해 전달되었다
- 이는 미국사회가 가족보다 지인이나 친구와 더 강한 연결을 가지는 것을 이유로 추정하고 이탈리아와 같이 친족간의 커뮤니케이션이 활발한 문화에서는 비율이 변할 수도 있다.
- 사회적 거리는 물리적 거리에 영향을 받지 않는다. 실제로 수백 피트 앞까지 전달된 편지가 최종적으로 전달되지 못한 채 끊기거나 거의 다 도착했는데 한참을 빙빙 돌다 마침내 도착한 경우도 볼 수 있었다.
추가적인 실험
- 정반대로 떨어져 있다고 생각하는 두 부류의 사람에게 전달하면 어떨까?
- 흑인-백인 사이를 전달하는 실험을 해보았다.
- 결과는 위와 동일하게 평균과 비슷한 5다리 정도로 나오게 되었다.
결론
Small World
- 서로 모르는 임의의 두 사람을 선택했을 때 약 5명의 사람만 거치면 서로에게 도달할 수 있다.
- 하지만 한가지 예외가 있다. A집단과 B집단이 완전히 격리되어있을 경우 A집단 내의 사람과 B집단 내의 사람은 절대 만날 수 없다는 것이다. 만약 섬에 사는 사람이 있고 이 섬은 육지와 교류가 일체 없다고 한다면 이 섬에 사는 사람은 육지사람과 절대 만날 수 없을 것이다.
느낀점
- 위 연구가 꽤 오래되고 편향에 대해 말이 많은 연구임에도 이 연구는 꽤나 의미가 있다
- 특히 우리가 실제로 특정 사람에게 물리적 혹은 실제로 도달하기 위해서는 약 5다리라고 하지만 사람을 그래프 위에 vertex로 나타냈을 때의 최단 거리와는 다르다고 생각한다.
- 본 연구에서도 나와있지만 내 생각에는 위 실험처럼 우리가 편지를 보낼 때 아무래도 편지를 조금 더 보내기 편한 사람을 기준으로 보냈을 것이고 예를 들어 직장상사, 편지를 주고받을 정도는 아닌 지인 등에게는 쉽게 보내지 못했을 것이다(비록 그 사람들이 더 적합해 보일지라도)
- 따라서 실제 그래프 상에서의 최단 거리는 이보다 같거나 오히려 적지 않을까라고 생각한다.
- 그럼에도 사실 이보다 유의미한 것은 그러한 최단거리가 아니라 실제로 우리가 사회적으로 도달할 수 있는 사회적 거리 라고 생각하고 앞으로의 연구 등에서도 이러한 사회적 거리를 구하는 연구가 필요하다고 생각한다
- 예를 들어 내가 별로 친하지 않은 친구(살면서 얼굴을 1번밖에 보지 않았다)의 지인이 BTS라고 한다. 또 내 절친의 사촌의 지인이 BTS라고 한다. 그렇다면 우리가 2다리를 거쳐서 BTS를 만나는 것이 빠를까 3다리를 거쳐서 BTS를 만나는 것이 빠를까에 대해 생각해보게 되었다.
