프로그래머스 피보나치 수

프로그래머스, 피보나치 수 문제

function solution(n) {
    const cache = [0,1] //피보나치 수열을 저장하는 공간
    
    //2번째 자리부터 시작하여 n까지의 수를 구하여야 하기 때문에 n+1
    for(let i=2; i < n+1; i++){
     	//2부터 시작하여 값을 cache에 넣고 그 값들로 다시 값을 구한다.
        cache.push((cache[i-2] + cache[i-1])%1234567)
    }
    return cache[n]
}

처음 부트캠프에서 피보나치 수열 알고리즘 보았을때는 풀이법을 봐도 이해가 잘 되지 않았는데, 다시 프로그래머스에서 피보나치 문제를 풀어보면서 이해가 되었다. 특히, 단순히 재귀로 푸는 것이 아니라 메모리에 저장하여 더 효율적으로 풀 수 있었다. 이해되지 않았던 캐쉬개념도 이해가 되며, 효율적인 코드를 작성할 수 있었다.

처음에는 단순하게 재귀함수로 풀어 보았다.

function solution(n) {
	if(n === 0) return 0
	if(n === 1) return 1

	return (solution(n-1) + solution(n-2))%1234567
}

피보나치 수는 0,1,1,2,3,5,8,13,21 ... 이런식으로 전의 수와 전전의 수를 더한 값이 계속 이어지는 수열이다.

처음 0과 1은 그대로 리턴하고 3번째 숫자(인덱스2)부터 규칙을 적용하여 재귀로 풀었다. 하지만, 큰 수가 들어갈 때는 재귀하는 횟수가 많아 콜스택 에러, 런타임 에러가 났다. 또, 함수를 한번 호출하면 두번의 호출을 더 하기 때문에 시간 복잡도는 O($2^n$)으로 매우 비효율적이다.

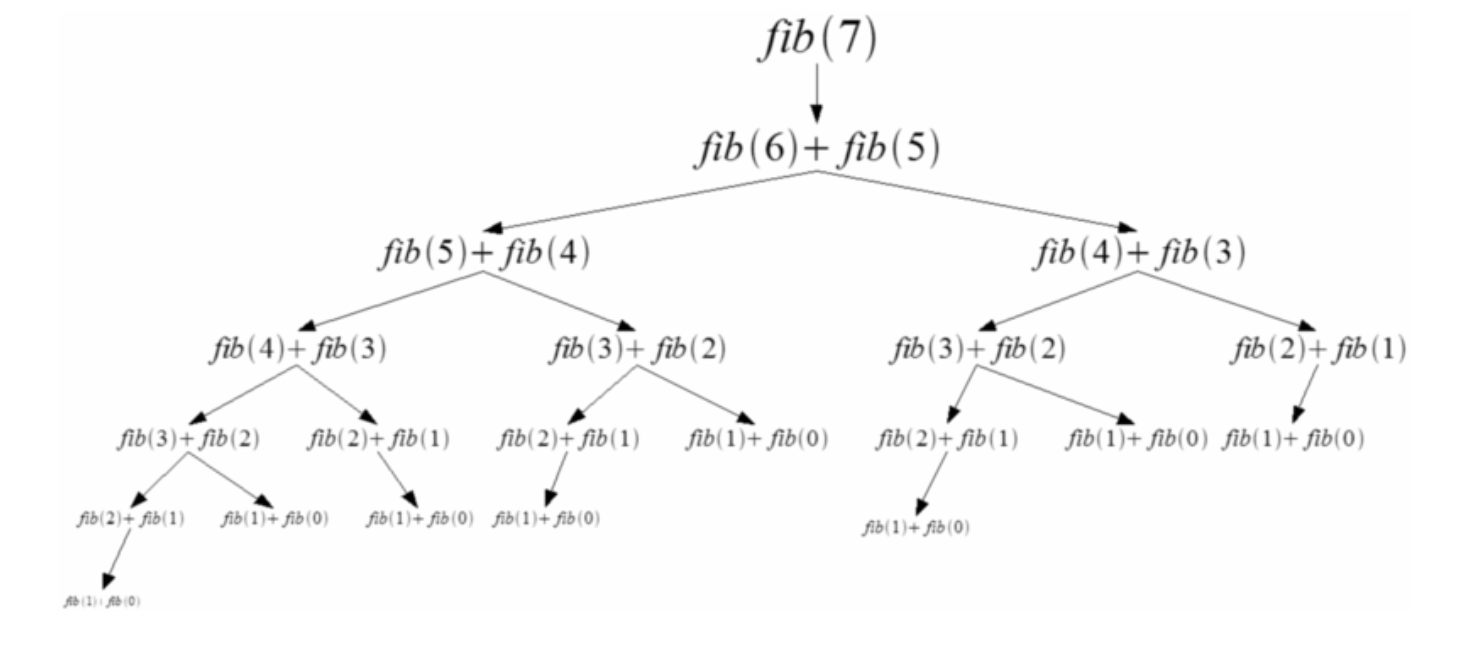
사진처럼 단지, 피보나치의 7번째 값을 구하기 위해서는 많은 계산 과정이 필요하다. 여기서 문제는 반복적인 계산 과정이 많다는 것이다. fib(3), fib(4) 등 반복적인 계산 과정이 많기 때문에 이미 구한 값들을 메모리에 저장하여 반복적인 과정을 없애면서 효율적인 코드를 작성할 수 있었다.

참고

피보나치