힙(heap)

• 완전 이진 트리에 있는 노드 중에서 키 값이 "가장 큰 노드"(max heap)나 키 값이 "가장 작은 노드"(min heap)를 찾기 위해서 만든 자료구조

개요

최대 힙(max heap)

• 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
• 부모 노드의 키 값 > 자식 노드의 키 값
• 루트 노드: 키 값이 가장 큰 노드

최소 힙(min heap)

• 최대 힙의 반대 개념

예시

<힙 구조 O>

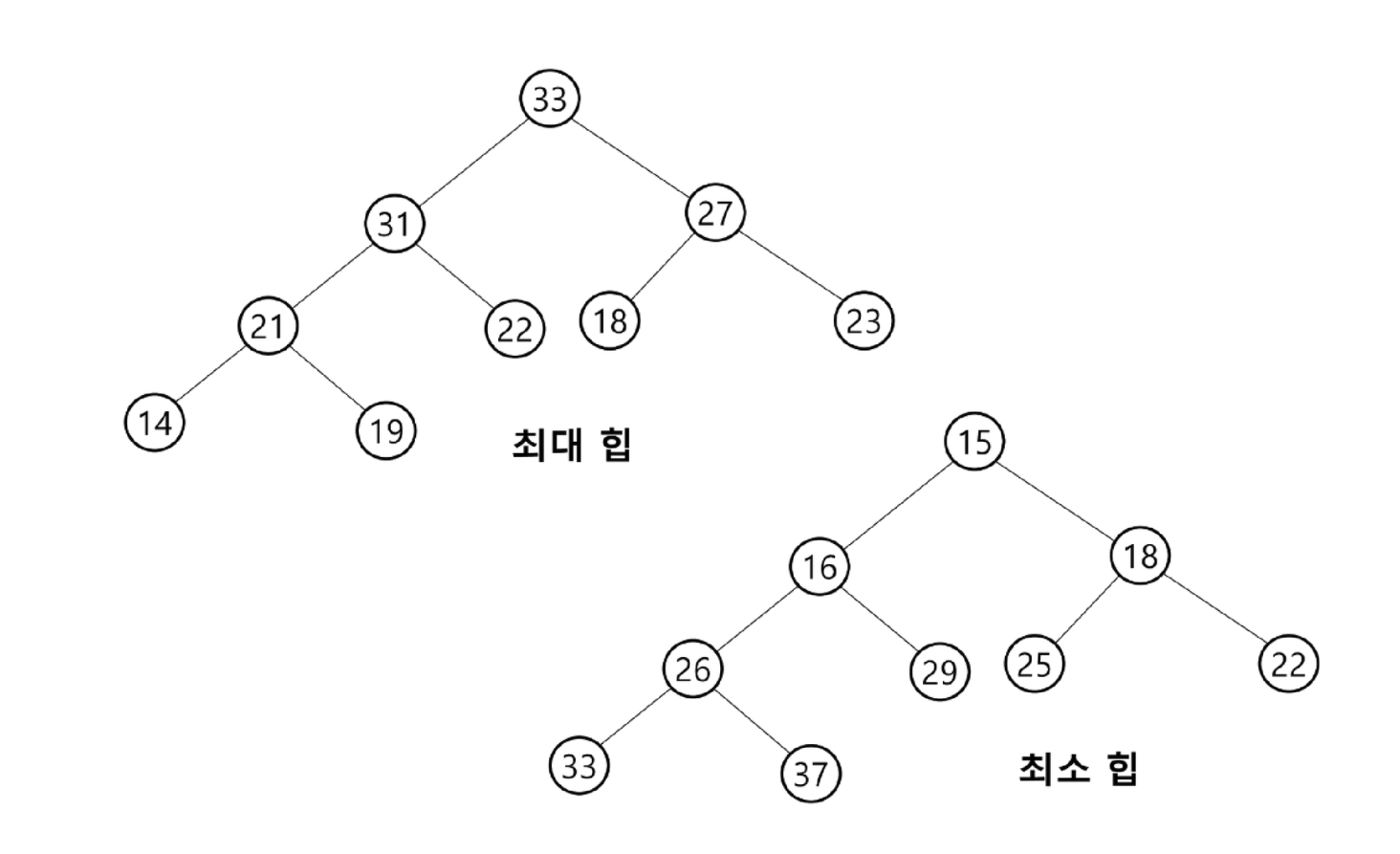
<힙 구조 X>

---

힙(heap) 연산

1. 삽입

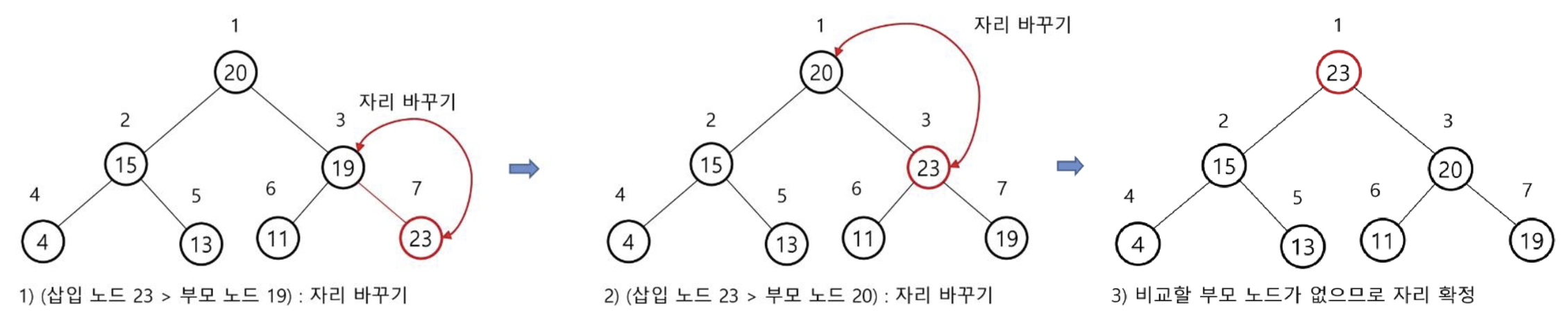
2. 삭제

---

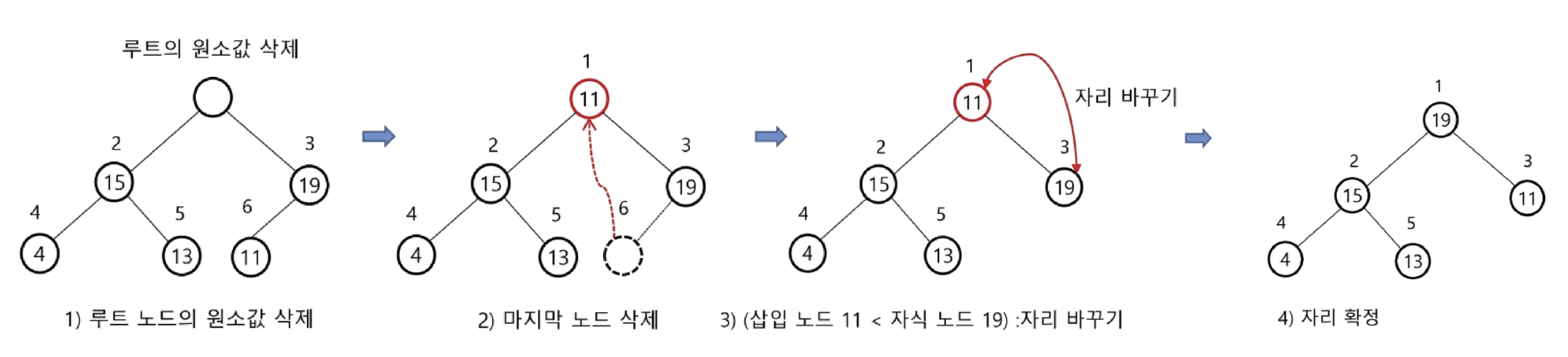
구현

class MaxHeap:
	def __init__(self):
		self.heap = []

	def heappush(self, item):
		self.heap.append(item)
		self._siftup(len(self.heap) - 1)

	def _siftup(self, idx):
		parent = (idx - 1) // 2
		while idx > 0 and self.heap[idx] > self.heap[parent]:
			self.heap[idx], self.heap[parent] = self.heap[parent], self.heap[idx]
			idx = parent
			parent = (idx - 1) // 2

	def heappop(self):
		if len(self.heap) == 0
			raise IndexError("힙이 비었습니다.")
		if len(self.heap) == 1:
			return self.heap.pop()
		root = self.heap[0]
		self.heap[0] = self.heap.pop()
		self._siftdown(0)
		return root

	def heapify(self, array):
		self.heap = array[:]
		n = len(array)
		for i in range(n // 2 - 1, -1, -1):
			self._siftdown(i)

	def _siftdown(self, idx):
		n = len(self.heap)
		largest = idx
		left = 2 * idx + 1
		right = 2 * idx + 2

		if left < n and self.heap[left] > self.heap[largest]:
			largest = left
		if right < n and self.heap[right] > self.heap[largest]:
			largest = right
		if largest != idx:
			self.heap[idx], self.heap[largest] = self.heap[largest], self.heap[idx]
			self._siftdown(largest)

heapq 모듈

• 최소 힙을 구현한 라이브러리
• 힙 함수 활용
  - heapq.heappush(heap, item) : item을 heap에 추가
  - heapq.heappop(heap) : heap에서 가장 왼쪽 원소를 pop
  - Heapq.heapify(x) : 리스트 x를 heap으로 변환 ( O(N) )

그러면 최대 힙은 어떻게? -> 값들을 모두 음수로 바꾸면 최소 힙으로 최대 힙처럼 사용 가능. 결과의 부호만 잘 처리하면 됨

우선순위 큐 (Priority Queue)

• 우선순위를 가진 항목들을 저장하는 큐
• FIFO 순서가 아니라 우선순위가 높은 순서대로 먼저 나가게 된다.
• 우선순위 큐를 구현하는 가장 효율적인 방법은 힙을 사용하는 것이다.
• 노드 하나 추가/삭제의 시간 복잡도가 O(logN) 이며, 최대값/최소값을 O(1)에 구할 수 있다.

예시

import heapq

priority_queue = []

heapq.heappush(priority_queue, (3, "3순위 작업"))
heapq.heappush(priority_queue, (1, "1순위 작업"))
heapq.heappush(priority_queue, (2, "2순위 작업"))

print(priority_queue)
# [(1, "1순위 작업"), (3, "3순위 작업"), (2, "2순위 작업")]

while priority_queue:
	task = heapq.heappop(priority_queue):
	print(task)

# (1, "1순위 작업")
# (2, "2순위 작업")
# (3, "3순위 작업")

백트래킹

개요

백트래킹 기법

• 어떤 노드의 유망성(promising)을 점검하여 유망하지 않다면 그 부모의 노드로 돌아가고(backtracking) 다음 자식 노드를 살핀다.
• 유망하다. = 해답이 될 가능성이 있다.
• 가지치기(pruning) = 유망하지 않다면 해당 노드를 가지 않는다. 나무(Tree)의 쓸모없는 가지를 치는 것.

백트래킹 절차

1. 상태 공간 트리의 깊이 우선 탐색(DFS)를 실시한다.
2. 각 노드가 유망한지 점검한다.
3. 만일 해당 노드가 유망하지 않으면, 그 노드의 부모 노드로 돌아가서 다른 노드 검색을 계속 진행한다.

백트래킹과 DFS 차이점

• DFS는 완전 탐색이다. 백트래킹은 가지치기를 통해 필요한 요소만 탐색한다. -> DFS를 pruning으로 최적화 하면 그게 백트래킹이다.

일반적인 코드 형태

def backtracking(node v):
	if promising(v):
		if there is a solution at v:
			find the solution
	else:
		for child of v:
			backtracking(child)