Codility Lesson 5-1: PassingCars

🤔 문제 분석

• N개의 int로 구성된 non-empty array A
• 연속된 원소는 도로 위의 연속된 자동차들을 의미
• 원소는 0 또는 1
  • 0: 동쪽으로 가는 차
  • 1: 서쪽으로 가는 차
• 목표는 교차하는 차의 pair를 세는 것
  • 교차하는 차의 쌍: (P, Q) (0 ≤ P(동쪽) < Q(서쪽) < N)
• 단, 쌍이 1,000,000,000개가 넘으면 -1 리턴

---

코딜리티 챕터 5는 Prefix Sums가 주제이다.

이 문제가 왜 구간합인지???????????❓ 꽤 오래 고민했다.

문제에서 요구하는 교차하는 차의 쌍은

동쪽으로 가는 차의 인덱스 P보다 큰! 인덱스 중에서, 서쪽으로 가는 차의 인덱스Q의 쌍이다.

그러니까 이게 또 무슨 말이냐면...

이런 말임. 배열 A의 구간 합은, 그 구간에서 서쪽으로 가는 차량의 수.

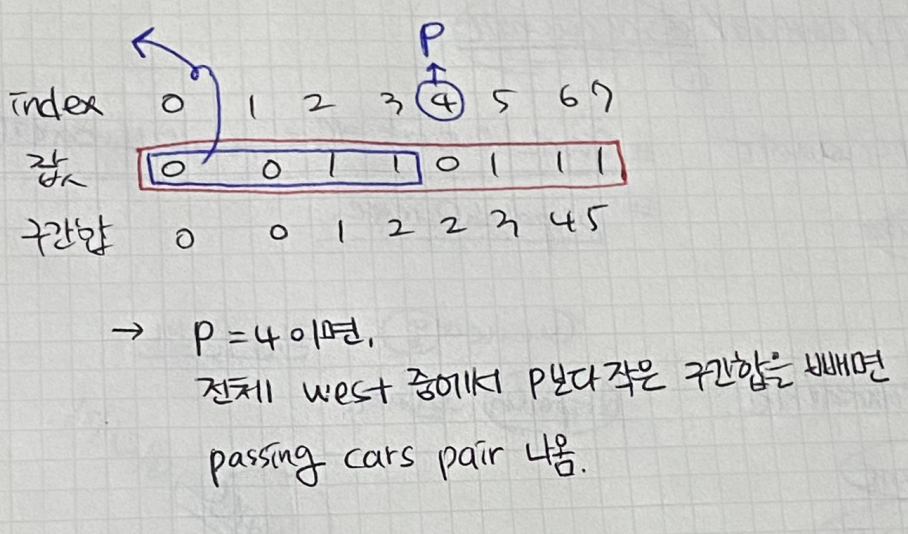
그런데 여기에서 P보다 Q가 무조건 커야 하니까,
서쪽으로 가는 전체 차의 합에서 Q 이전에 나타난 차들을 뺴주면 된다.

그렇게되면 원소 N개를 가진 Array A와 임의의 Q가 주어졌을 때 Q와 쌍을 이룰 수 있는 차량의 합 pairsAtQ는

pairsAtQ = 구간합[N] - 구간합[Q-1]

✍️ solution

첫 번째 시도

public func solution51(_ A : inout [Int]) -> Int {
    // 1의 누적합이 west의 갯수! -> prefixSums
    
    // prefixSums구하기 O(n)
    let count = A.count
    var pSum = Array(repeating: A[0], count: count)
    for i in 1..<count {
        pSum[i] = pSum[i-1] + A[i]
    }
    
    // 누적 구간합 구하기
    var totalPassingCount = 0
    for (index, value) in A.enumerated() {
        if value == 0 {
            let passingCount = pSum[count - 1] - (index == 0 ? 0 : pSum[index - 1])
            totalPassingCount += passingCount
        }
    }
    return totalPassingCount
}

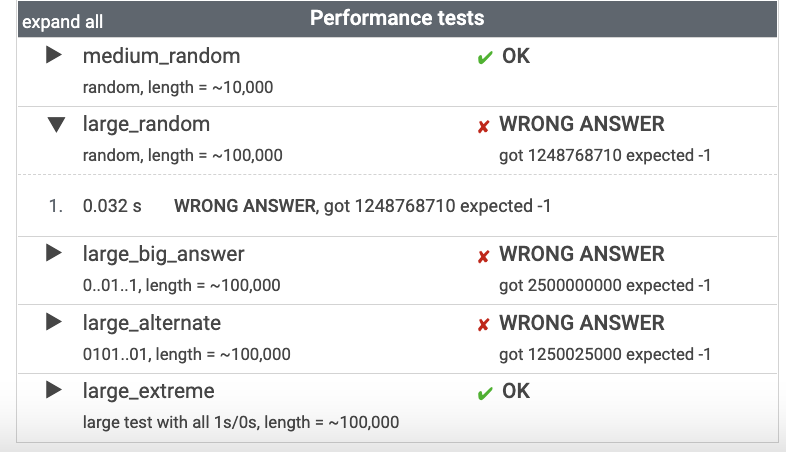
결과: 70%
놓친 부분은 아래의 예외 조건을 적어주지 않았다...👇
- 단, 쌍이 1,000,000,000개가 넘으면 -1 리턴

예외 조건 충족 해주기

public func solution51(_ A : inout [Int]) -> Int {
    // 1의 누적합이 west의 갯수! -> prefixSums
    
    // prefixSums구하기 O(n)
    let count = A.count
    var pSum = Array(repeating: A[0], count: count)
    for i in 1..<count {
        pSum[i] = pSum[i-1] + A[i]
    }
    
    // 누적 구간합 구하기 O(1)
    var totalPassingCount = 0
    for (index, value) in A.enumerated() {
        if value == 0 {
            let passingCount = pSum[count - 1] - (index == 0 ? 0 : pSum[index - 1])
            totalPassingCount += passingCount
            // 1000000000쌍이 넘었을 때 예외처리
            if totalPassingCount > 1000000000 {
                return -1
            }
        }
    }
    return totalPassingCount
}

결과: 100%

🍫끝

🔖 출처

• Codility Lessons 5.1: PassingCars