# 복잡도Complexity

❓확장성Scalability

• 데이터베이스 관점에서 확장성은 데이터베이스에서 저장이나 검색하는 데에 얼마나 오랜 시간이 걸리는지에 대한 것이다.
• 알고리즘에서, 확장성은 input 크기가 증가함에 따라 실행 시간과 메모리 사용 측면에서 알고리즘이 어떻게 수행되는지를 의미한다.
• 작은 양의 데이터에서는 expensive 알고리즘도 빠르게 느껴지지만, 데이터가 늘어남에 따라 expensive 알고리즘은 주체할 수 없어진다.

✍️ 오늘 배울 것

• 실행시간과 메모리 사용의 관점에서, 다양한 수준에 따른 Big O notation

# 시간 복잡도Time complexity

• 작은 양의 데이터에서는 요즘 기기들의 성능이 워낙 좋아서 expensive 알고리즘도 빠르게 느껴진다.
• 하지만 데이터가 증가하면, expensive 알고리즘의 비용이 증가하는 것이 확실히 보인다.
• time complexity는 인풋사이즈가 증가함에 따라 알고리즘이 동작하는 데에 필요한 시간의 척도이다.
• 여기에서는 일반적인 시간복잡도를 배우고, 어떻게 식별하는지identify 배운다.

1. Constant time

• Constant time algorithm: 인풋 사이즈와 상관없이 일정하게 걸리는 시간

func checkFirst(names: [String]) {
  if let first = names.first {
    print(first)
  } else {
    print("no names")
  }
}

• names배열의 사이즈는 이 함수가 동작하는 데에 아무런 영향도 미치지 않는다.
• names에 10개가 들어있든, 100만개가 들어있는 이 함수는 오직 배열의 첫 번째 원소만을 확인한다.

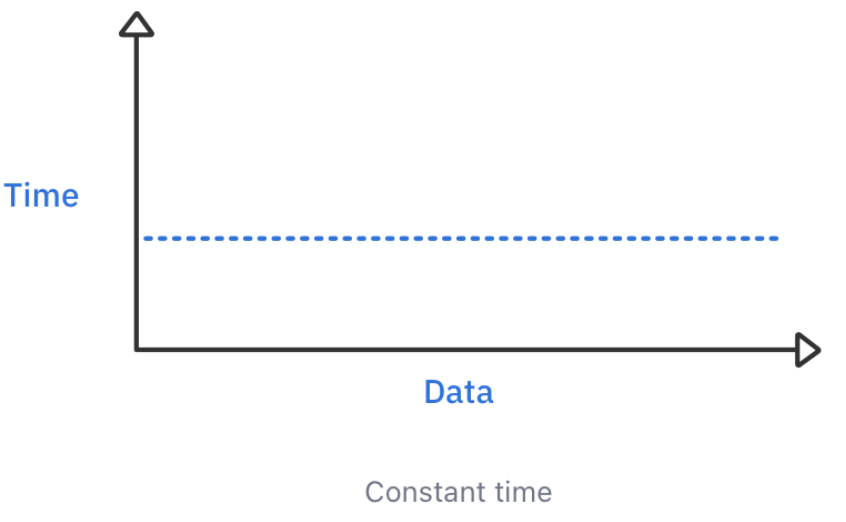
🌠출처 - raywenderlich - Data structures algorithms in swift v.4.0

• Big O notation: 시간 복잡도의 다양한 크기를 간단하게 나타내기 위해 사용하는 표기법
• Constant time complexity ⇒ O(1)
  
  

2. Linear time

func printNames(names: [String]) {
  for name in names {
    print(name)
  }
}

• 여기에서는 배열의 크기가 증가함에 따라, 그 크기만큼 for loop의 반복 횟수가 증가한다.

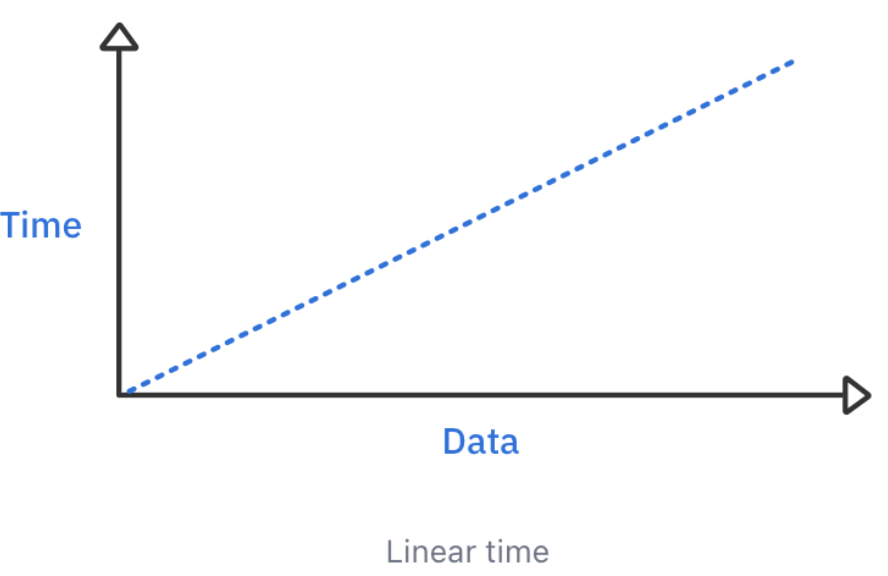
🌠출처 - raywenderlich - Data structures algorithms in swift v.4.0

• Linear time complexity ⇒ O(n)
  
  

🙋 두 개의 루프를 돌면서, 여섯개의 O(1)을 호출한다면, O(2n+6)?

👉 time complexity는 성능의 high-level shape를 말한다. 따라서 루프가 몇 개인지는 계산하지 않는다. 모든 상수는 Big O notation에서 삭제된다. O(2n+6)은 O(n)과 같다.

비록 이 책의 중심적인 관심사는 아니지만, 절대 효율을 위한 최적화는 중요할 수 있다. 기업들은 Big O notation이 무시하는 상수의 경사slope를 줄이기 위해 연구 개발에 수백만 달러를 쏟아부었다. 예를 들어 GPU에 최적화된 알고리즘(O(n))은 일반 CPU 버전 알고리즘(O(n) )보다 100배 더 빨리 실행될 수 있다. 비록 우리는 이런 종류의 최적화는 무시하겠지만, 이런 속도조절은 중요하다.

3. Quadratic time

• n squared
• 인풋 사이즈의 제곱 만큼 소요된다.

func printNames(names: [String]) {
  for _ in names {
    for name in names {
      print(name)
    }
  }
}

• names 배열을 돌면서, 모든 원소들을 출력한다.
• 만약 10개의 이름이 원소로 있다면, 10번 돌면서 10개를 출력하기 때문에 시간복잡도는 10*10 = 100이다.
• 이전의 시간복잡도들과 다르게, Quadratic time은 데이터 사이즈의 증가에 따라 빠르게 통제를 벗어날 수 있다.

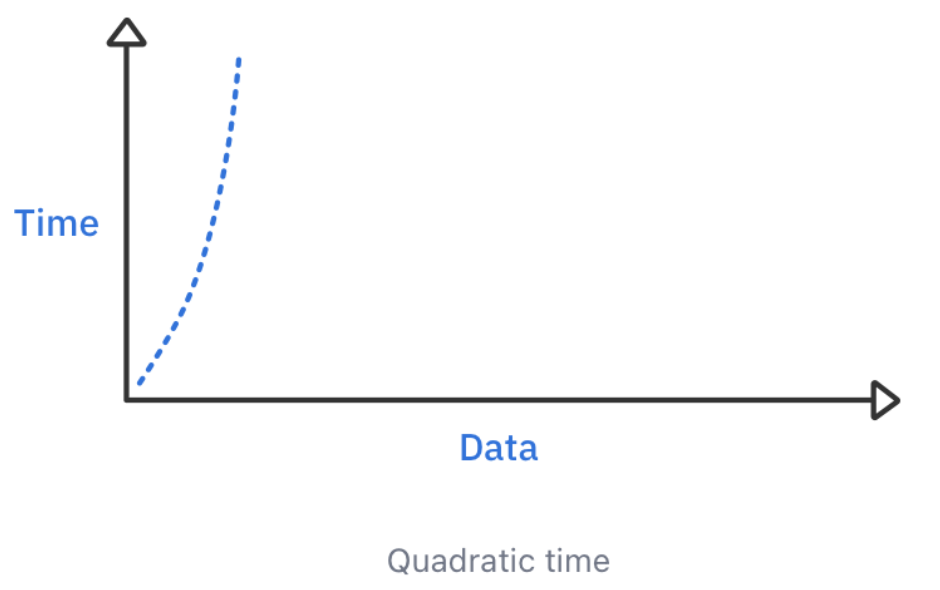
🌠출처 - raywenderlich - Data structures algorithms in swift v.4.0

• Quadratic time complexity ⇒ O(n²)
• linear time algorithm이 언제나 quadratic time algorithm보다 빠르다.
  
  

4. Logarithmic time

• 지금까지는 모든 원소를 한 번 이상 검사하는 시간 복잡도였다.
• 원소들의 일부만을 검사해서 더 빠른 런타임을 가져오는 방법도 있다.
• 인풋 데이터에 일부 가정을 함으로써 지름길을 가져온다.
• 예를 들어서, 정렬된sroted 배열의 경우, 특정 값이 들어있는지 검사하는 가장 빠른 방법은?
• 일반적으로는 결론에 다다를 때까지 모든 원소를 검사하는 linear algorithm을 이용하고, 이는 O(n)이다. 이 역시 좋지만, 정렬된 배열의 경우에는 더 좋은 솔루션이 있다.

let numbers = [1, 3, 56, 66, 68, 80, 99, 105, 450]

func naiveContains(_ value: Int, in array: [Int]) -> Bool {
  for element in array {
    if element == value {
      return true
    }
  }

  return false
}

• 중간 값을 확인하여, 필요한 비교의 횟수를 절반으로 줄일 수 있다.

func naiveContains(_ value: Int, in array: [Int]) -> Bool {
  // array가 비어있으면 false를 리턴하고 종료
  guard !array.isEmpty else { return false }

  let middleIndex = array.count / 2

  if value <= array[middleIndex] {
    for index in 0...middleIndex {
      if array[index] == value {
        return true
      }
    }
  } else {
    for index in middleIndex..<array.count {
      if array[index] == value {
        return true
      }
    }
  }

  return false
}

• 중간 값을 비교한 후, 배열 원소들의 절반 만을 비교한다.
  

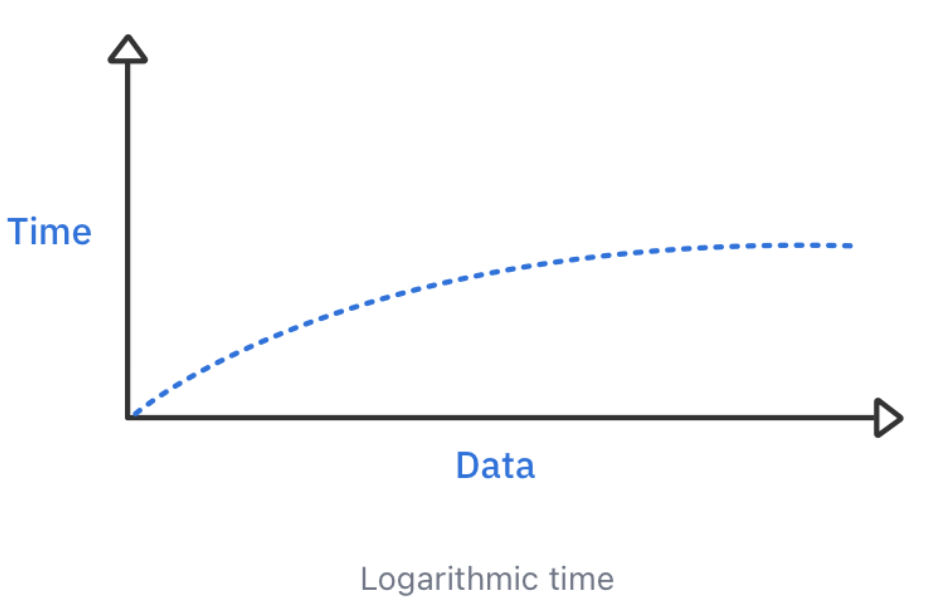
🌠출처 - raywenderlich - Data structures algorithms in swift v.4.0

• 인풋 데이터가 증가할수록, 더 많은 효과가 나타난다.
• approach horizontal
• 이런 알고리즘이 필요한 상황은 거의 없지만, 매우 강력하다.
• Logarithmic time complexity ⇒ O(log n)

🙋 로그 베이스 2 ? 10 ?

👉 로그 베이스는 2. 하지만 성능의 모양shape이 핵심이므로, 로그 베이스는 중요하지 않다.

5. Quasilinear time

• linear time보다는 성능이 좋지 않지만, quadaratic time보다는 월등하다.
• 이는 일반적으로 사용하게 될 알고리즘이다.
• sort
• Quasilinear time complexity ⇒ O(n log n)
  • multiplication of linear and logarithmic time
  • 성능: logarithmic < quasilinear < linear
• linear보다 성능이 좋지 않지만, 많은 다른 유형의 복잡도에 비해 좋다.

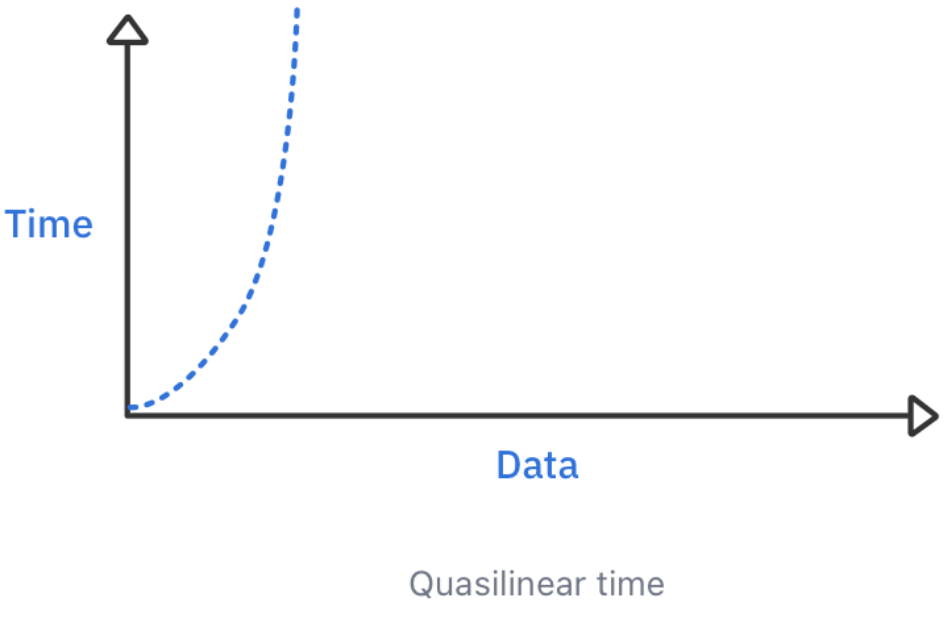
🌠출처 - raywenderlich - Data structures algorithms in swift v.4.0

• quadratic과 모양이 유사하지만, 그렇게 드라마틱하게 증가하지는 않는다.
• 그래서 큰 데이터 셋에 상대적으로 회복력resilient이 있다.
  
  

6. Other time complexities

• polynomial time, exponential time, factorial time, ...
• time complexity는 high-level overview of performance이다.
• 이를 통해 알고리즘의 속도를 판단할 수 없다. → 같은 시간 복잡도를 가지고 있더라도, 속도가 다를 수 있다.
  
• 작은 데이터 셋에서는 이는 실제 속도의 정확한 척도가 아닐 수 있다.

  → 작은 데이터 셋의 경우, 메모리 할당은 알고리즘에서 비교해야 하는 원소의 수보다 많은 비용이 들 수 있다.

  
  

7. Comparing time complexity

func sumFromOne(upto n: Int) -> Int {
  var result = 0
  for i in 1...n {
    result += i
  }
  return result
}

sumFromOne(upto: 10000)

• 위 함수의 시간 복잡도는 O(n)

func sumFromOne(upto n: Int) -> Int {
  (1...n).reduce(0, +)
}
sumFromOne(upto: 10000)

• 위 함수의 시간 복잡도 역시 O(n)
• 위의 두 함수의 시간 복잡도는 같지만 아래의 함수가 실행 속도가 더 빠르다. 그 이유는 표준 라이브러리에 compiled code이기 때문이다.

func sumFromOne(upto n: Int) -> Int {
  (n + 1) * n / 2
}
sumFromOne(upto: 10000)

• 위 함수의 시간 복잡도는 O(1)
• 상수 시간 복잡도는 언제나 낫다.
  
  

🔖 출처

• Raywenderlich - Data structures algorithms in swift v4.0