
학교강의에서 언급된 방법들을 정리한 글입니다.
네이버 블로그에 포스팅한 글 중 가장 조회수가 높았던, 끊임없이 검색 유입되었던 글이다. 딥러닝을 접하는 누구라도 꼭 한 번은 만나게 될 과적합 문제. 2020년도 1학기 통계학과 딥러닝 전공수업을 수강하면서 얻은 팁들을 이곳에도 공유하고자 한다.
1. 서론
딥러닝 모델을 돌리다보면 필연적으로 만나게 되는 과적합...오버피팅...overfitting...
좋은 모델을 만드는건 모델의 성능을 높이는 것이고, 이는 과적합을 해결하는 것과 상당한 연관성을 가진다. 과적합 없이 성능을 높이는게 핵심이기 때문이다. 하지만, 모델의 층을 늘릴수록, 즉 더욱 깊은 모델을 구성할수록 필요한 파라미터(모수)의 개수가 늘어나고, 이렇게 되면 train data에만 딱 들어맞지, 처음 보는 test data를 집어넣었을 땐 엉망진창인 모델이 될 가능성이 커진다.
일반적으로 과적합은 모델 학습과정에서 valid loss가 지속적으로 감소하다가 증가하는 지점부터 발생한다고 정의된다. 과적합 없이 모델의 성능을 높이는건 상당히 어려운 일이다. 하이퍼파라미터(초모수)를 조정하며 지속적으로 train과 valid loss, accuracy를 점검해야하는데, 말이 쉽지 하이퍼파라미터 조정하는게 특히 처음 접하는 입장에선 어디부터 어떻게 손을 대야할지 막막한 부분이다.
통계학을 전공하시는 교수님(열정 of 열정맨)은 딥러닝의 고질병 overfitting 문제를 통계학의 관점에서 풀고자 여러 방면으로 고민을 하셨고, 이를 매주 제출하는 과제에 피드백으로 제시해주셨다. 따라서, 이제 언급할 해결책 중 몇 가지는 중요한 통계학적 의미를 내포하고 있다.
2. 본론
그래서 과적합을 어떻게 해결하느냐.
물론! 가장 좋은 방법은 train data의 양을 늘리는 것!
그러나 우리가 데이터를 늘리고 싶다해서 늘릴 수 있는게 아니겠지요,,, data augmentation(데이터 증식) 방법도 있긴 하지만 이건 순수 데이터를 늘리는게 아니라 train 데이터를 가공해서 새로운 버전을 만드는 방법이기 때문에 논외로 두겠다.
과적합은 모수가 많아질수록 심화된다. 층이 깊어질 수록(layer 가 늘어날 수록) 모수가 늘어날 수 밖에 없는데.. 그럼 1개의 layer로만 모델을 구성해야하는건가..? 그건 "Deep" learning이라고 할 수 없는데? 적게는 3~4개, 많게는 수십개의 층을 쌓아야 하기 때문에 여러가지 규제 기법들을 활용하여 과적합을 해소하고자 하는 것이다. 차례로 만나보도록 하자.
2.1. Dropout (드롭아웃)
랜덤으로 노드를 꺼버리자. 파라미터(모수) 무시해버리기~
학회강의에서 말하기로는 뉴럴넷이 알코올을 먹은 것 마냥 중간 노드 학습을 끊어버리는 방법이다. 입력값의 일부를 0으로 두기 때문에 역전파시 파라미터 업데이트가 되지 않고, 이는 모형의 불확실성을 증가시켜 과적합 해결에 기여한다.
드롭아웃 비율은 경험적으로 판단할 일, 과적합이 심하지 않다면 0.2~0.5 사이를 추천하고 너무 심하다 싶으면 과감하게 0.8로 설정해보자.
층마다 비율을 얼마나 다르게 해야할지에 대해서도 고민이 될 수 있는데, 나의 경우에는 노드 수가 많은 층의 드롭아웃 비율을 우선적으로 높여준다. 노드 수가 많다는 것은 그만큼 생겨나는 모수가 많아진다는 것이고 이는 과적합을 심화시킬 수 있기 때문이다.
물론 드롭아웃만 한다고 해서 과적합을 해결할 수 있는건 아니다. 아래 등장할 regularization 등의 방법과 같이 적절하게 써야한다. stackoverflow 사이트에 여러 사람들의 경험치가 묻어난 질문과 답변이 많으니 이 부분은 끊임없이 구글링하며 공부하는것이 좋겠다.
2.2. L1(Lasso)/L2(Ridge) Regularization
학습에 기여하지 못하는 모수를 0으로 만들어버리자~
아래 수식과 같이 손실함수에 람다항을 추가해서 일종의 페널티를 주는 방법이다.
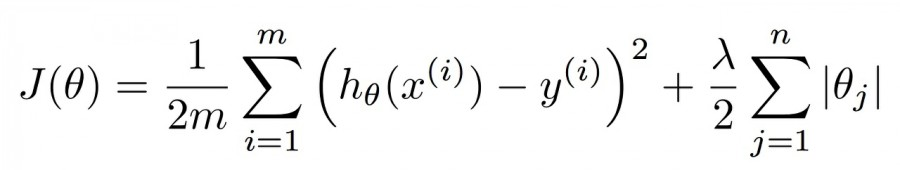 L1 Regularization(절댓값)
L1 Regularization(절댓값)
 L2 Regularization(제곱)
L2 Regularization(제곱)
자세한 증명은 이 블로그를 참고하길 바란다.
내가 기록하고 싶은 내용은 regularization을 가급적 출력층에 사용하는 것이 좋다는 것이다. 교수님께서는 regularization이 통계학의 가설검정과 유사하다고 하셨는데, 가설검정 시 t값이나 F값, 혹은 p-value를 통해 유의미한 변수인지 아닌지를 판단하는 것처럼 regularization은 loss를 줄이는데 기여하지 못하는 모수를 0(L1) 또는 0에 가까운(L2) 값으로 제한하는 기능을 한다. 보통 L2 regularization이 L1보다 더 많이 쓰인다. 실제로 적용해봤을 때 효과가 두드러지게 나타난 규제기법이었다.
여기서 잠깐!
<Q. Dropout과 Regularization을 동시에 사용해야 하는가?>
이 질문에 대한 답변은 교수님 버전과 구글링 버전이 달라서 혼란스러웠다.
- 교수님: 두 기법은 상호보완관계, 하나만 쓰면 안되고 둘 다 써야한다.
- 구글링: 두 기법은 상호보완 관계, 보통 둘 다 쓰는게 성능이 더 높은데 하나만 쓸지 둘 다 쓸지는 경험적으로 판단할 문제다. 즉, 케바케! 데바데!
실제 실험을 해보았을 때에는 구글링 답변처럼 모델마다 결과가 달랐다. 어떤 모델은 두 기법 모두 쓰는게 효과가 좋았고 또 어떤 모델은 하나씩만 쓰는게 더 좋았다. 개인적으로 구글링 입장에 동의하고, 일반적으로 둘 다 쓰는게 성능이 더 높다고는 하니 둘 다 실험해보는 것을 추천한다!
2.3. 출력층 직전 은닉층의 노드 수를 줄여라.
출력직전 모수를 줄이는게 가장 효과가 좋다. 왜냐구?
통계학에서 오버피팅을 해결하는 방법은 쓸데없는 변수를 제거해서 입력변수 x의 수를 줄이는 것인데(t-test 등을 통해 significant하지 않은 변수를 제거한다) 통계학의 관점에서 출력층 직전 은닉층 노드 수는 설명변수의 수가 된다. 따라서 의미있는 설명변수들을 남기기 위해/생성하기 위해 출력직전 노드 수를 확 줄여버리는 것이다.
교수님이 고안해내신 교수님만의 방법이라고 하시길래, 상당히 신빙성 있어서 실제로 써봤는데 대체로 잘 먹힌다!
나는 주로 출력 범주의 수가 20이하인 경우, FCL(Fully Connected Layer) 마지막 층의 노드 수를 32로 줄인다. 만약 출력 범주의 수가 100 이상으로 넘어갈 경우엔 그에 맞춰서 마지막 층 노드 수를 결정한다.
cf) 비슷한 이야기로 과적합을 막으려면 모수(parameter)의 수를 줄여야 하는데, 은닉층 자체를 줄이거나 은닉층 노드 수를 줄이면 된다. 이때 터무니없이 막 줄이면 안되고, 조절해보면서 적당한 선을 찾아야 한다. CNN에서는 kernel size, pooling size, filter 수를 줄이면 된다.
2.4. Batch Normalization(배치정규화)
뉴럴넷에서 각 활성함수의 미분값은 역전파 과정에서 계속 곱해지기 때문에 굉장히 중요하다. 시그모이드 함수의 경우 일정수준 이상 혹은 이하의 값이 입력되었을때 미분값이 0에 가깝게 되는데, 이때 파라미터 업데이트과정에서 0에 가까운 값이 지속적으로 곱해지면 vanishing gradient(기울기 소실) 문제가 발생한다. 이렇게 되면 파라미터 업데이트가 거의 일어나지 않고 수렴 속도도 아주 느리게 되어 최적화에 실패하게 되는데, 이 문제를 해결하는 방법으로는 배치정규화 외에도 relu 등의 활성함수를 사용하거나 가중치 초기화(weight initialization)을 적용하는 방법이 있다.
배치정규화는 mini batch 별로 분산과 표준편차를 구해 분포를 조정한다. 역전파시 파라미터 크기에 영향을 받지 않기 때문에 좋다고 한다.
배치정규화는 각 은닉층에서 활성함수 적용 직전에 사용되어야한다. 일반적으로 선형결합-배치정규화-활성함수-드롭아웃 순으로 은닉층 연산이 진행된다.
2.5. 그 외 참고하면 좋을 사항들
1. epoch의 증가는 과적합 해결을 위한 수단이 아니라 모니터링 수단이다.
단순하게 epoch만 늘려주면 train data의 loss는 줄고 accuracy는 높아지기 때문에 train data의 loss와 accuracy는 valid 결과와 비교하기 위한 참고사항일 뿐이다. epoch 수를 늘리면 valid와 train loss가 교차하는 지점이 발생한다. 일반적으로 valid loss가 감소하다가 증가하는 시점을 과적합으로 정의하기 때문에 이 지점에서 적당한 epoch을 결정한다. 이는 early stopping과도 관련이 있다.
2. epoch이 증가하면서 train loss 와 valid loss가 수렴해야 가장 좋다.
교차점에서 epoch을 결정하더라도 train과 최종 test loss와 accuracy를 비교해야한다. 이러한 점검은 cross-validation으로 진행해야한다.
3. batch_size는 과적합과 관련이 없다. 모수의 수렴 문제와 관련이 있다.
배치사이즈가 작을 수록 수렴속도는 느리지만 local minimum에 빠질 가능성은 줄어든다. 반면 배치사이즈가 클 수록 학습진행속도와 수렴속도가 빨라지지만 항상 빨리 수렴하는 것은 아니다. 작은 데이터셋이라면 32가 적당하다고 하는데 이 역시도 구글링하다보면 수많은 의견들이 존재한다. 적당히 참고해가면서 실험해보면 좋겠다.
3. 결론
대부분의 규제 기법들은 모형의 불확실성을 증가시켜 일반화에 용이하도록 만드는 것이었다. 이 원리를 이해하면 흩어져있던 개념들이 한 데 모을 수 있을 것이다.
위 방법들을 사용하면 과적합은 해소되는데 문제는 모델의 전체적인 성능이 상당히 하락하는 경우가 있다. 1학기에 수행했던 과제 기준으로는 코랩에서 10 에폭까지만 학습시키기 때문에 이 문제가 더 두드러지는데, 사실 에폭을 상당히 많이 늘린다면, 즉 학습을 더 오래 시키면 성능이 더 오를 것이라 생각한다. 그리고 실제 모델 학습시킬때 10 에폭은 터무니 없이 작은 수치다..ㅎ 하지만 코랩의 gpu 사양으로 에폭을 크게 두는건...무리이긴 하다.
딥러닝은 명확한 정답이 없어서 더 어렵게 느껴지지만 과적합에 지지 않도록 다양한 방법을 시도해보도록 하자! 화이팅!
저도 공부하고 있는 입장이라 피드백은 언제나 환영입니다. 혹여 제가 잘못 이해하고 있는 부분이 있다면 지적해주세요.
안녕하세요! 좋은 글 감사합니다. 그런데 질문이 있습니다. 배치 사이즈가 작을수록 어째서 극소점에 빠질 확률이 줄어드는 것일까요? 데이터를 조금씩 보기 때문에 오히려 더 극소점에 빠질 수 있을거라고 생각했는데 궁금합니다..