[Algorithms] Stack, Queue, DFS, BFS
DFS, BFS를 이해 전 스택, 큐, 재귀함수를 알아야 하는데 재귀함수는 이미 블로그 포스팅이 되어 있으니 스택 큐를 간단하게 정리해보고 시작하려고 합니다.
Stack
- 스택의 큰 특징은 후입선출(LIFO) 가장 최근에 들어온 데이터가 가장 먼저 나가는 개념이다.
public static void main(String[] args) {
// 스택 생성
Stack<Integer> stack = new Stack<>();
// 스택에 원소 추가 (push)
stack.push(1);
stack.push(2);
stack.push(3);
// 스택에서 원소 제거 (pop)
int poppedElement = stack.pop();
// 스택 맨 위의 원소 확인 (peek)
int topElement = stack.peek();
// 스택이 비어있는지 확인
boolean isEmpty = stack.isEmpty();
// 스택의 크기 확인
int size = stack.size();
}
}
Queue
- 큐는 스택과 반대로 선입선출(FIFO) 가장 처음 들어온 데이터가 먼저 나가는 개념
public class SimpleQueueExample {
public static void main(String[] args) {
// 큐 생성
Queue<String> queue = new LinkedList<>();
// 큐에 원소 추가 (offer)
queue.offer("Alice");
queue.offer("Bob");
queue.offer("Charlie");
// 큐에서 원소 제거 (poll)
String removedElement = queue.poll();
// 큐 맨 앞의 원소 확인 (peek)
String frontElement = queue.peek();
// 큐가 비어있는지 확인
boolean isEmpty = queue.isEmpty();
// 큐의 크기 확인
int size = queue.size();
}
}
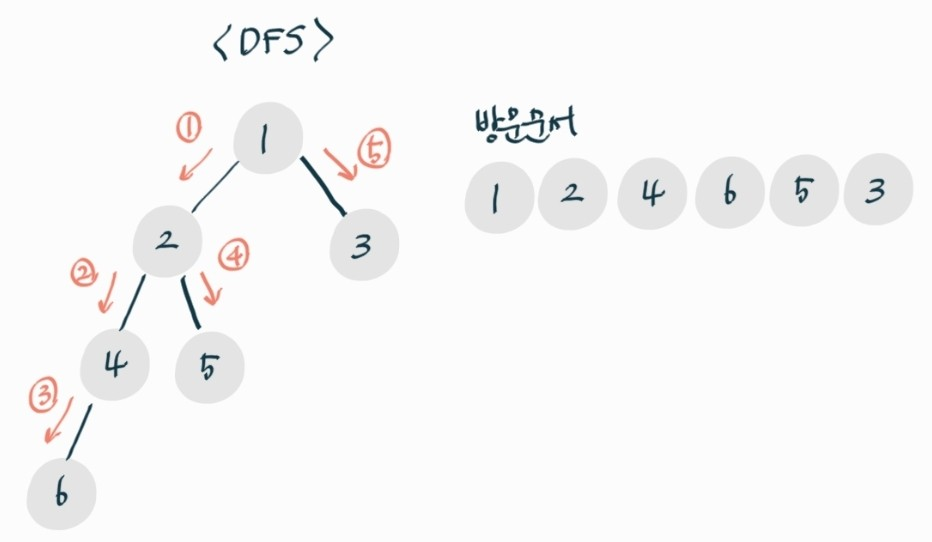
DFS (Dreadth-First Search)
깊이 우선 탐색
-
시작 정점 방문 후 다음 분기로 넘어가기 전 해당 분기 완벽하게 탐색
-
스택, 재귀함수 두 가지 방법으로 풀 수 있다.
-
일반적으로 재귀함수를 통해 구현한다.
-
모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
-
너비 우선 탐색보다 좀 더 간단함
-
검색 속도 자체는 너비 우선 탐색에 비해서 느림
-
장점
최선의 경우 빠르게 해를 찾음 -
단점
찾은 해가 최적 해가 아닐 가능성이 있음
최악의 경우 해를 찾는데 시간이 가장 오래 걸린다.
class Graph {
private int V;
private LinkedList<Integer> adj[]; // 링크드리스트의 배열
// constructor
Graph (int v) {
V = v;
adj = new LinkedList[v];
// v개의 LinkedList 선언 및 생성
for (int i = 0; i < v; ++i) {
adj[i] = new LinkedList();
}
}
void addEdge (int v, int w) { // v번째 LinkedList 에 w를 삽입
adj[v].add(w);
}
// DFS 함수
void DFS(int v) { // v를 시작노드로!
boolean visited[] = new boolean[V]; // 각 노드이 방문 여부를 저장하기 위해
DFSUtil(v, visited);
}
// DFS에서 호출되는 함수
void DFSUtil(int v, boolean visited[]) {
// 현재 노드를 방문한 것으로 체크 (visited의 v번째 요소를 true로)
visited[v] = true;
System.out.println(v + " ");
// 방문한 노드와 인접한 모든 노드를 가지고 온다
Iterator<Integer> it = adj[v].listIterator();
while (it.hasNext()) {
int n = it.next();
// 방문하지 않은 노드면 해당 노드를 다시 시작 노드로하여 DFSUtil을 호출
if (!visited[n])
DFSUtil(n, visited); // 재귀호출!
}
}
}
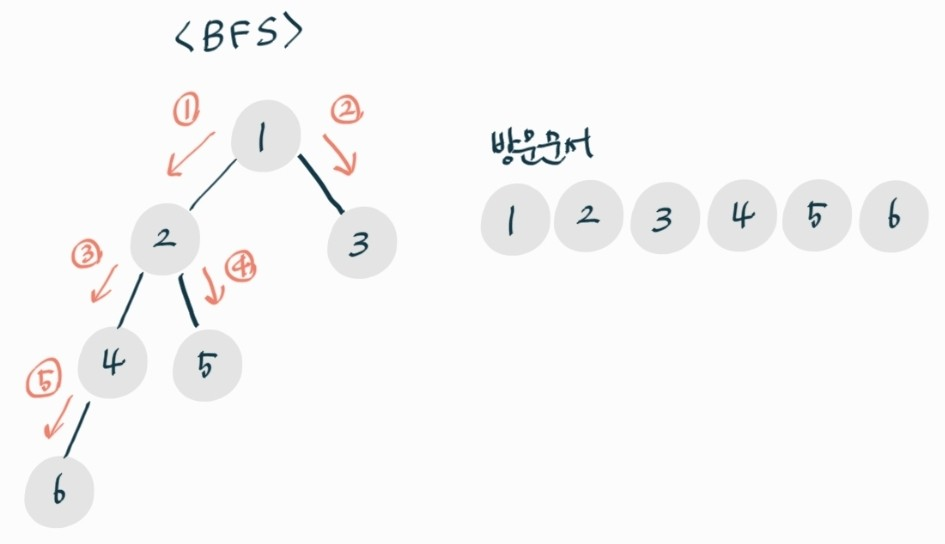
BFS(Breadth-First Search)
너비 우선 탐색
- 시장 정점 방문 후 가까운 정점 우선 방문
- 큐를 사용해서 문제를 풀 수 있다.
- 장점
최적 해 찾음 보장 - 단점
최소 실행보다 오래 걸림
class Graph {
private int V;
private LinkedList<Integer> adj[]; // 링크드리스트의 배열
// constructor
Graph (int v) {
V = v;
adj = new LinkedList[v];
// v개의 LinkedList 선언 및 생성
for (int i = 0; i < v; ++i) {
adj[i] = new LinkedList();
}
}
void addEdge (int v, int w) { // v번째 LinkedList 에 w를 삽입
adj[v].add(w);
}
// DFS 함수
void BFS(int s) {
boolean visited[] = new boolean[V]; // 각 노드이 방문 여부를 저장하기 위해
LinkedList<Integer> queue = new LinkedList<Integer>();
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
// 방문한 노드를 큐에서 추출하고 값을 출력
s = queue.poll();
System.out.println(s + " ");
// 방문한 노드와 인접한 모든 노드를 가져온다.
Itertor<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
// 방문하지 않은 노드면 방문한 것으로 표시하고 큐에 삽입
if (!visited[n]) {
visited[n] = true;
queue.add();
}
}
}
}
}
알고리즘에 약해서 코테를 더 많이 풀어보면서 공부를 해야 될거같다..
참고
https://developer-mac.tistory.com/64
https://velog.io/@lucky-korma/DFS-BFS%EC%9D%98-%EC%84%A4%EB%AA%85-%EC%B0%A8%EC%9D%B4%EC%A0%90
https://velog.io/@smallcherry/Java-AlgorithmBFSAndDFS
