[자료구조] 그래프 입문

맹쥐·2025년 4월 3일

정글-개발일지

목록 보기

15/24

현실 세계는 관계의 연속이다.
사람과 사람, 도시와 도시, 웹페이지와 웹페이지 사이처럼 수많은 객체들이 복잡하게 연결되어 있다.

이런 관계를 표현하기에 가장 적합한 자료구조가 바로 "그래프(Graph)”이다.

1. 그래프란?

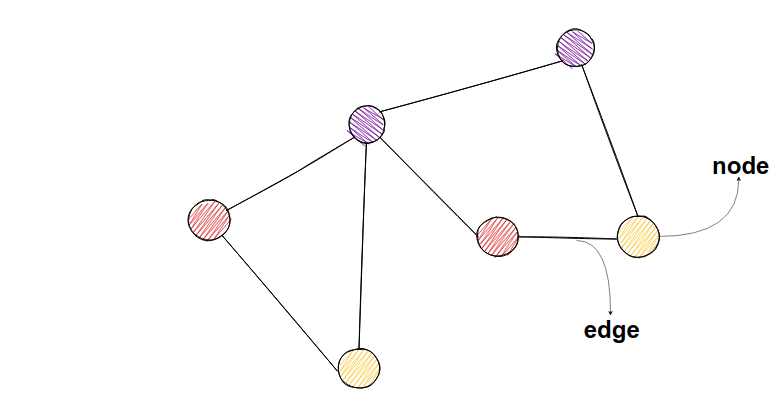
그래프는 정점(Vertex, Node)과 간선(Edge)의 집합입니다. 정점은 데이터를 담는 단위이고, 간선은 정점 간의 관계를 표현한다. 예를 들어, SNS에서 유저는 정점, 친구 관계는 간선이다.

2. 그래프의 종류

그래프는 간선의 방향성과 가중치에 따라 여러 가지로 나눌 수 있다.

무방향 그래프(Undirected Graph): 간선에 방향이 없다. A와 B가 연결되어 있으면 A→B, B→A 양방향으로 이동 가능하다.
방향 그래프(Directed Graph, Digraph): 간선에 방향이 있다. A→B는 존재하지만 B→A는 아닐 수도 있다.
가중치 그래프(Weighted Graph): 간선에 숫자값(거리, 비용 등)이 부여된다. 길 찾기, 네트워크 비용 계산 등에 활용됩니다.
비가중치 그래프(Unweighted Graph): 간선마다 동일한 비용 또는 비용을 고려하지 않는 그래프이다.
연결 그래프(Connected Graph)
- 그래프의 모든 정점이 하나로 이어져 있음 (직접 또는 간접 연결)
비연결 그래프(Disconnected Graph)
- 일부 정점이 다른 정점과 전혀 연결되지 않음
사이클 있음: 시작점과 끝점이 같은 경로가 존재 (3개 이상의 정점 필요)

사이클 없음(Acyclic): 어떤 경로도 자기 자신으로 되돌아오지 않음

🙋🏻‍♀️ DAG란 ?

DAG는 Directed Acyclic Graph의 약자로, 방향성이 있으면서 사이클이 없는 그래프를 의미한다.

Directed: 간선에 방향이 있음 (A → B)

Acyclic: 어떤 정점에서 시작해서 다시 자기 자신으로 돌아오는 사이클(순환)이 없음

즉, "돌고 돌지 않는 단방향 그래프"이다.

예를들어, 강의 선수 과목 시스템에 사용된다.

수강하려면 먼저 들어야 하는 과목이 있는 경우 (예: 알고리즘 → 머신러닝)

🧠 DAG의 특징

특징 설명
사이클 없음 절대 순환 불가. 무한 루프 발생 X
정점 간 순서 존재 A → B라면, A가 B보다 먼저 일어나야 함
위상 정렬 가능 선후 관계가 있는 정점들을 정렬 가능
그래프 탐색이 안전 무한 루프 걱정 없이 DFS/BFS 가능

특징	설명
사이클 없음	절대 순환 불가. 무한 루프 발생 X
정점 간 순서 존재	A → B라면, A가 B보다 먼저 일어나야 함
위상 정렬 가능	선후 관계가 있는 정점들을 정렬 가능
그래프 탐색이 안전	무한 루프 걱정 없이 DFS/BFS 가능

3. 그래프 표현 방법

그래프는 크게 두 가지 방식으로 구현할 수 있다.

📌 인접 행렬(Adjacency Matrix)

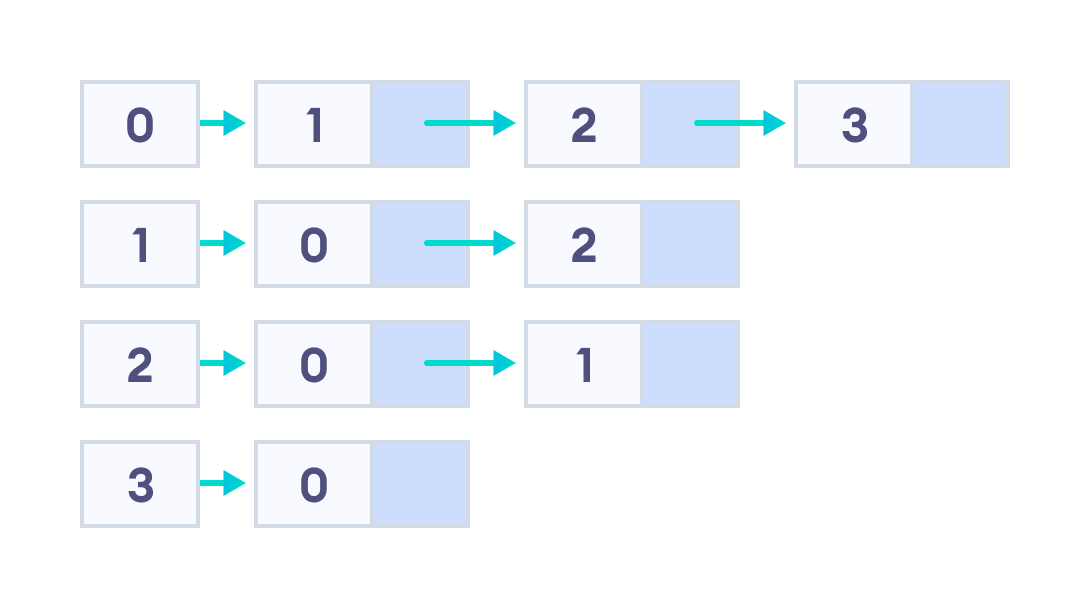
- n개의 정점이 있을 때 n x n 2차원 배열을 사용한다.
- [i][j]가 1이면 i번 정점에서 j번 정점으로 간선이 있다는 의미이다.
- 간선을 빠르게 확인할 수 있으나, 메모리 사용량이 많고 희소 그래프에는 비효율적이다.

📌 인접 리스트(Adjacency List)

- 각 정점마다 연결된 정점 목록을 리스트로 저장한다.
- 메모리 효율이 뛰어나고, 대부분의 경우 인접 리스트가 선호된다.

4. 그래프의 핵심 용어

정점(Vertex): 데이터를 담는 노드이다.
🔹 노드(Node)란?

노드 = 데이터를 저장 + 다른 노드와의 연결 정보를 담는 단위

자료구조에 따라 모양은 조금씩 다르지만, 공통적으로는 아래 두 가지 정보를 가진다.
1. 데이터(Data): 해당 노드가 담고 있는 값
2. 포인터 또는 연결 정보: 다음 노드를 가리키거나(연결 리스트), 연결된 노드 목록을 갖는 구조(트리나 그래프)
간선(Edge): 정점 간의 연결이다.
차수(Degree): 정점에 연결된 간선의 수이다. 방향 그래프에서는 진입 차수(In-degree)와 진출 차수(Out-degree)를 나눈다.
경로(Path): 정점들을 잇는 간선의 연속이다.
사이클(Cycle): 시작점과 끝점이 같은 경로이다.
연결 그래프(Connected Graph): 모든 정점이 연결되어 있는 그래프이다.
트리(Tree): 사이클이 없고 연결된 그래프입니다. n개의 정점이 있다면 n-1개의 간선을 가진다.
DAG(Directed Acyclic Graph): 방향이 있고 사이클이 없는 그래프이다. 작업 순서 정리 등 위상 정렬에서 많이 활용된다.