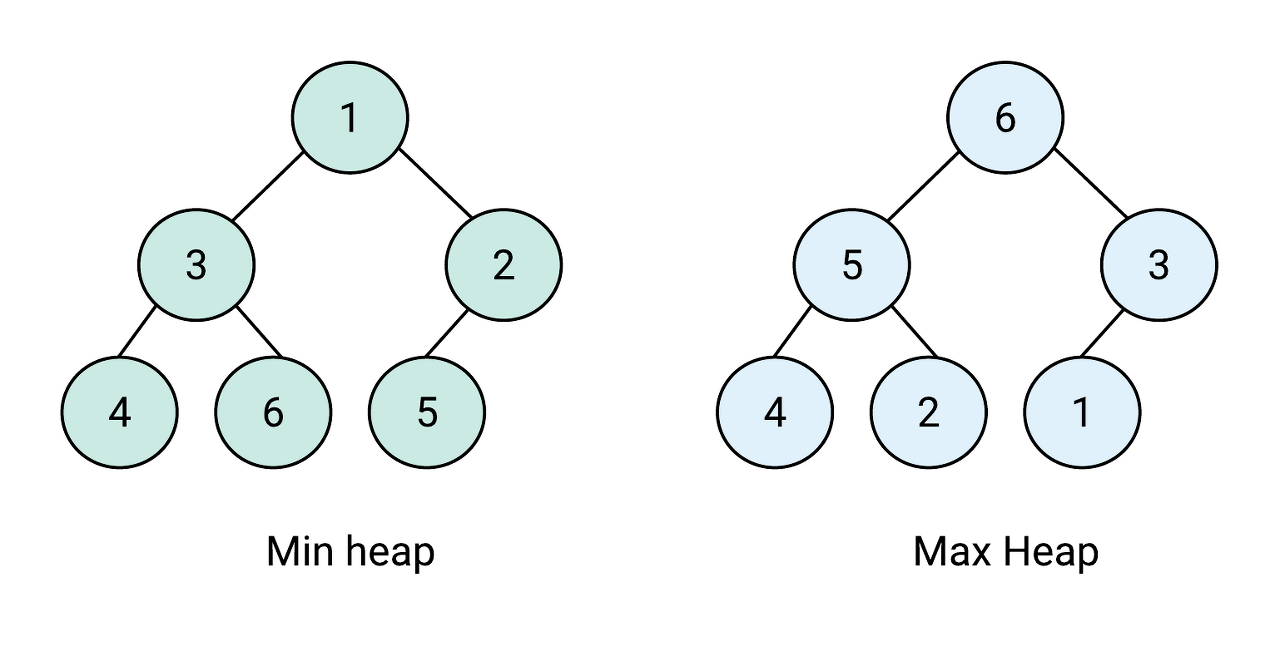
💡 우선순위 큐 & 힙 관계

• 우선순위 큐는 "동작 방식"에 가까운 개념
  • → 우선순위 높은 것 먼저 꺼내자
• 힙은 "이걸 구현하는 실제 자료구조"

우선순위 큐를 효율적으로 만들기 위해 → "힙"이라는 자료구조를 이용하는 것이다.

우선순위 큐(추상 자료형)
 └── 힙으로 구현하는 경우가 많음 (O(log N))

---

☑️ 힙이란?

• 완전 이진트리의 일종으로 우전순위 큐를 위하여 만들어진 자료구조이다.
• 부모와 자식 간의 우선순위 규칙 유지
  (부모 ≤ 자식 → 최소 힙 / 부모 ≥ 자식 → 최대 힙)
• 배열로도 표현 가능

---

☑️ 이진 탐색 트리 (BST) vs 힙 (Heap)

구분	이진 탐색 트리 (BST)	힙 (Heap)
정렬 기준	왼쪽 < 부모 < 오른쪽 (이진 탐색 성질)	부모 ≤ 자식 (Min Heap) / 부모 ≥ 자식 (Max Heap)
탐색 목적	빠른 탐색 (검색)	빠른 "최댓값" or "최솟값" 추출
탐색 시간	O(log N) - 원하는 값 찾기	O(1) - 루트가 항상 최댓값 or 최솟값
트리 구조	보통 비균형 가능 (skewed)	항상 완전 이진 트리 (좌→우로 꽉 채움)
활용	검색, 정렬된 데이터 관리	우선순위 큐 (priority queue)

---

✅  힙의 유형

1️⃣ 최소 힙 (Min-Heap)

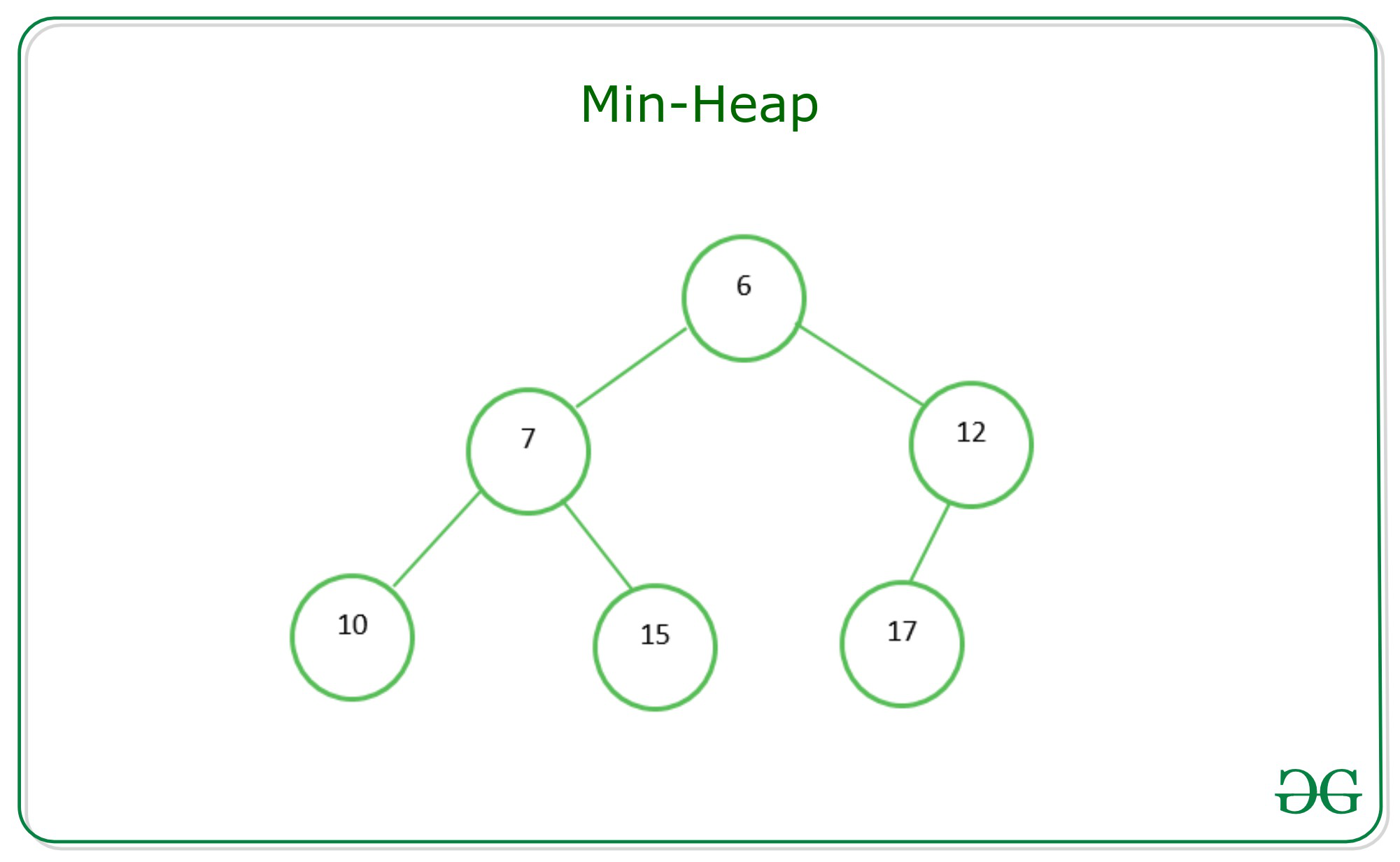
• 부모 ≤ 자식

2️⃣ 최대 힙 (Max-Heap)

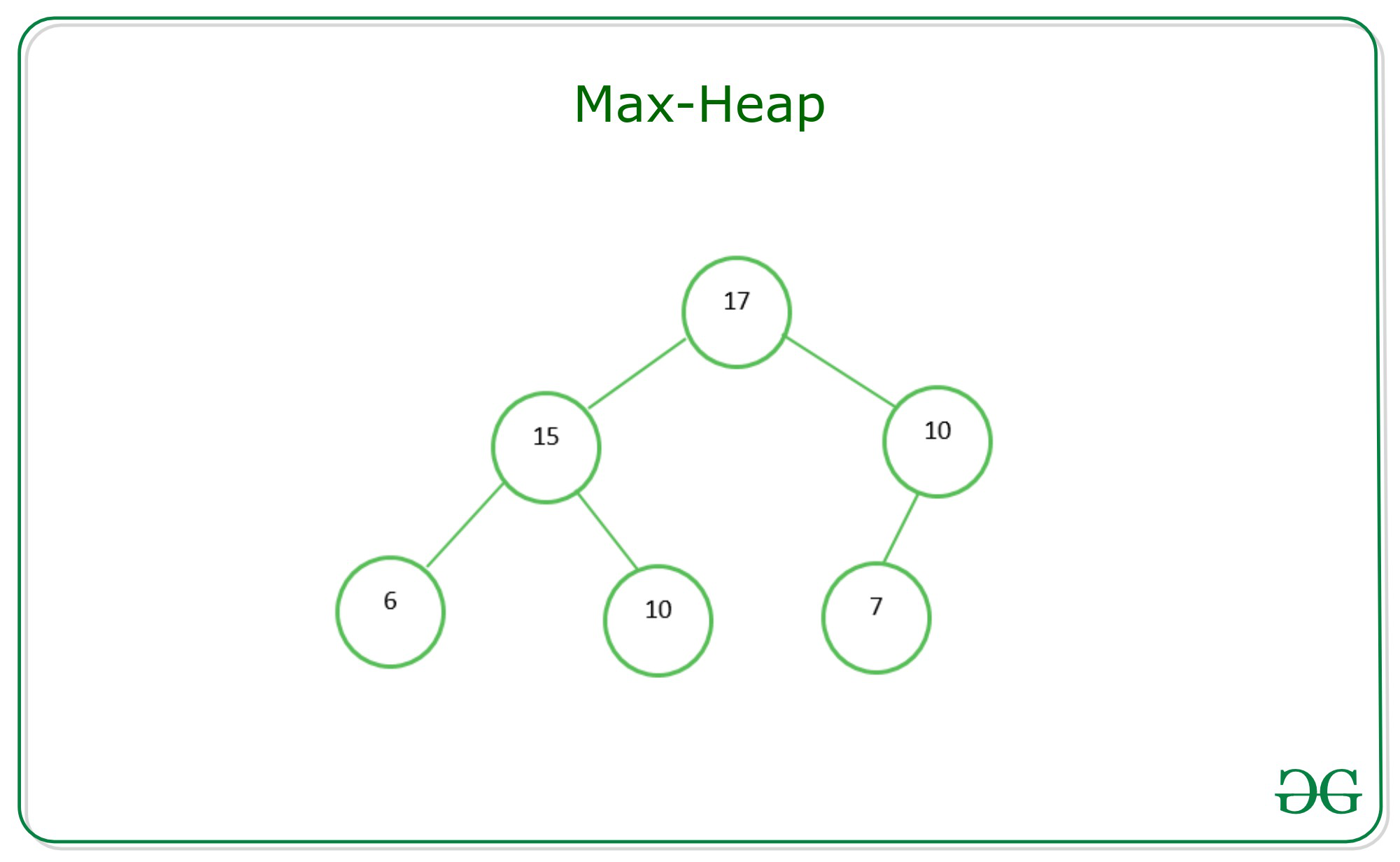
• 부모 ≥ 자식

---

 heapq란?

파이썬 표준 라이브러리에서 제공하는

힙 기반의 우선순위 큐 모듈

• Min-Heap 형태로 동작 (항상 "가장 작은 값"이 루트)
• 내부적으로 리스트 기반의 완전 이진 트리 구조 사용

---

☑️ heapq 기본 사용법

import heapq

pq = []
heapq.heappush(pq, 5)
heapq.heappush(pq, 3)
heapq.heappush(pq, 7)

print(heapq.heappop(pq))  # 3 (가장 작은 값부터 나옴)

---

✅ 주요함수

1) heapq.heappush(리스트, 값)

→ 힙에 값 삽입

2) heapq.heappop(리스트)

→ 힙에서 최솟값 추출

3) heapq.heapify(리스트)

→ 일반 리스트를 힙으로 변환

---

☑️ heapify는 어떻게 동작하는가?

arr = [7, 3, 5, 2, 8]
heapq.heapify(arr)
print(arr)  # [2, 3, 5, 7, 8] (heap 형태로 재정렬)

‘heapify’ 는 주어진 리스트를 한 번에 힙 구조로 재정렬하는 함수이다.

힙 구조로 재정렬된 리스트는 일반적인 오름차순 정렬이 아닌, 부모 ≤ 자식 관계를 만족하는 트리 형태로 배열된다. 이 과정을 통해 리스트가 힙으로 변환되며 이후 heappush, heappop 등의 힙 연산이 가능해진다.

---

☑️ 그렇다면 heapq를 어떻게 처음부터 구현해야 할까?

1. 빈 리스트를 준비한다.
2. heapq.heappush()로 값을 하나씩 넣어가며 힙 구조를 만들어 나간다.
3. 이후 heapq.heappop()으로 항상 최솟값을 뽑아가며 사용한다.

예시 구현

import heapq

# Step 1: 빈 힙 준비
pq = []

# Step 2: 값 삽입 (삽입할 때마다 자동으로 heapify-up 수행)
heapq.heappush(pq, 9)
heapq.heappush(pq, 4)
heapq.heappush(pq, 6)
heapq.heappush(pq, 2)
heapq.heappush(pq, 7)

# Step 3: 최솟값부터 하나씩 pop
while pq:
    print(heapq.heappop(pq))

이 코드에서는 삽입할 때마다 O(log N)의 시간복잡도로 자동으로 힙 구조가 유지된다.

---

☑️ 직접 힙을 구현하면 어떻게 되는가?

파이썬의 heapq 모듈 대신 직접 힙을 구현할 수도 있다. 대표적인 방법은 다음과 같다.

직접 구현한 Min-Heap 예시

class MinHeap:
    def __init__(self):
        self.heap = [0]  # 0번 인덱스는 비워두어 인덱스 계산을 편하게 함

    def push(self, val):
        self.heap.append(val)
        self._heapify_up(len(self.heap) - 1)

    def pop(self):
        if len(self.heap) <= 1:
            return None
        if len(self.heap) == 2:
            return self.heap.pop()
        root = self.heap[1]
        self.heap[1] = self.heap.pop()
        self._heapify_down(1)
        return root

    def _heapify_up(self, idx):
        while idx > 1 and self.heap[idx] < self.heap[idx // 2]:
            self.heap[idx], self.heap[idx // 2] = self.heap[idx // 2], self.heap[idx]
            idx //= 2

    def _heapify_down(self, idx):
        while idx * 2 < len(self.heap):
            min_child = self._get_min_child(idx)
            if self.heap[idx] > self.heap[min_child]:
                self.heap[idx], self.heap[min_child] = self.heap[min_child], self.heap[idx]
                idx = min_child
            else:
                break

    def _get_min_child(self, idx):
        if idx * 2 + 1 >= len(self.heap):
            return idx * 2
        if self.heap[idx * 2] < self.heap[idx * 2 + 1]:
            return idx * 2
        else:
            return idx * 2 + 1

직접 힙을 구현하면 동작 원리를 깊이 이해할 수 있으며, 필요에 따라 Max-Heap 또는 커스텀 힙을 만들어낼 수 있다.