대표적인 자료구조의 예시
선형 구조: 자료가 순서를 가지고 연속되어 있음
ex) 스택, 큐
비선형 구조: 선형 구조에 해당하지 않는 자료구조
ex) 트리, 그래프
트리에 대해 알아보기 전에, 간단하게 그래프부터 알아보도록 하자.
그래프
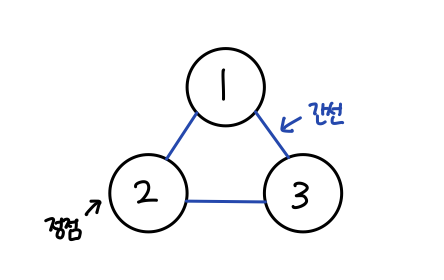
특징
- 정점(vertex)과 간선(edge)으로 이루어져 있는 자료구조
- 정점: 자료, 상태 등 뭔가를 담고 있음 ('노드'라고도 한다.)
- 간선: 정점 간의 관계를 나타냄 - 방향이 있을수도, 없을 수도 있다.
방향이 있는 간선을 포함한 그래프를 유향 그래프라고 한다.
- 경로: 어떤 정점에서 다른 정점에서 이동하기 위해 거치는 모든 정점
ex) 정점 3에서 정점 1로 이동하는 경로 중 하나는 3 - 1- 사이클: 어떤 정점에서 출발하여 자기 자신의 정점으로 다시 돌아오는 경로
ex) 정점 3의 사이클 중 하나는 3 - 2 - 1 - 3
트리
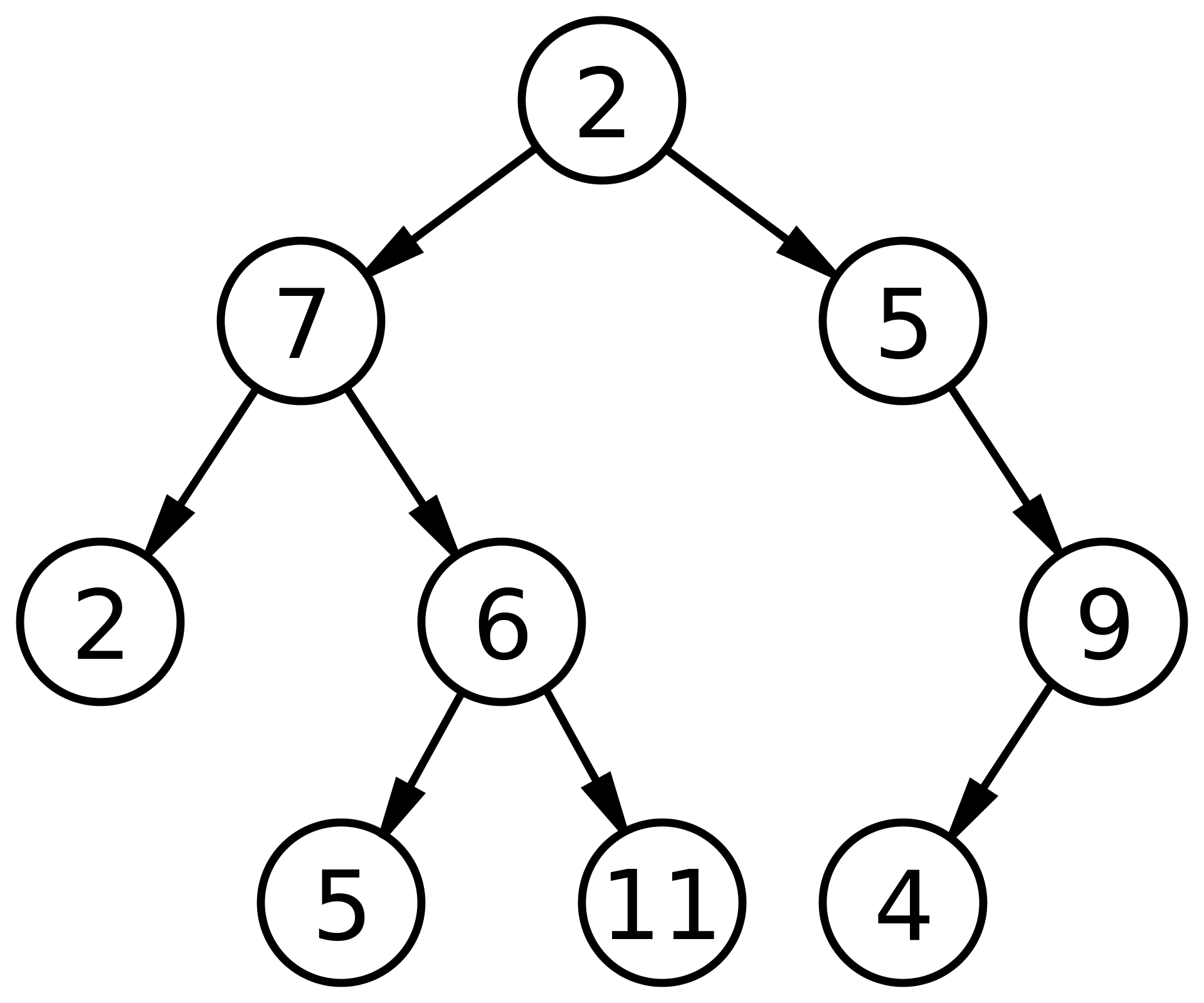
그래프 중에서도 아래의 특별한 성질을 갖는 그래프를 트리라고 한다.
특징
- 트리의 간선들은 모두 방향성을 갖는다.
- 어떤 정점을 가리키는 정점의 개수는 최대 1개이다.
- 어떤 정점에서 다른 정점으로 이동할 수 있는 경로는 1개다.
- 트리는 사이클을 갖지 않는다.
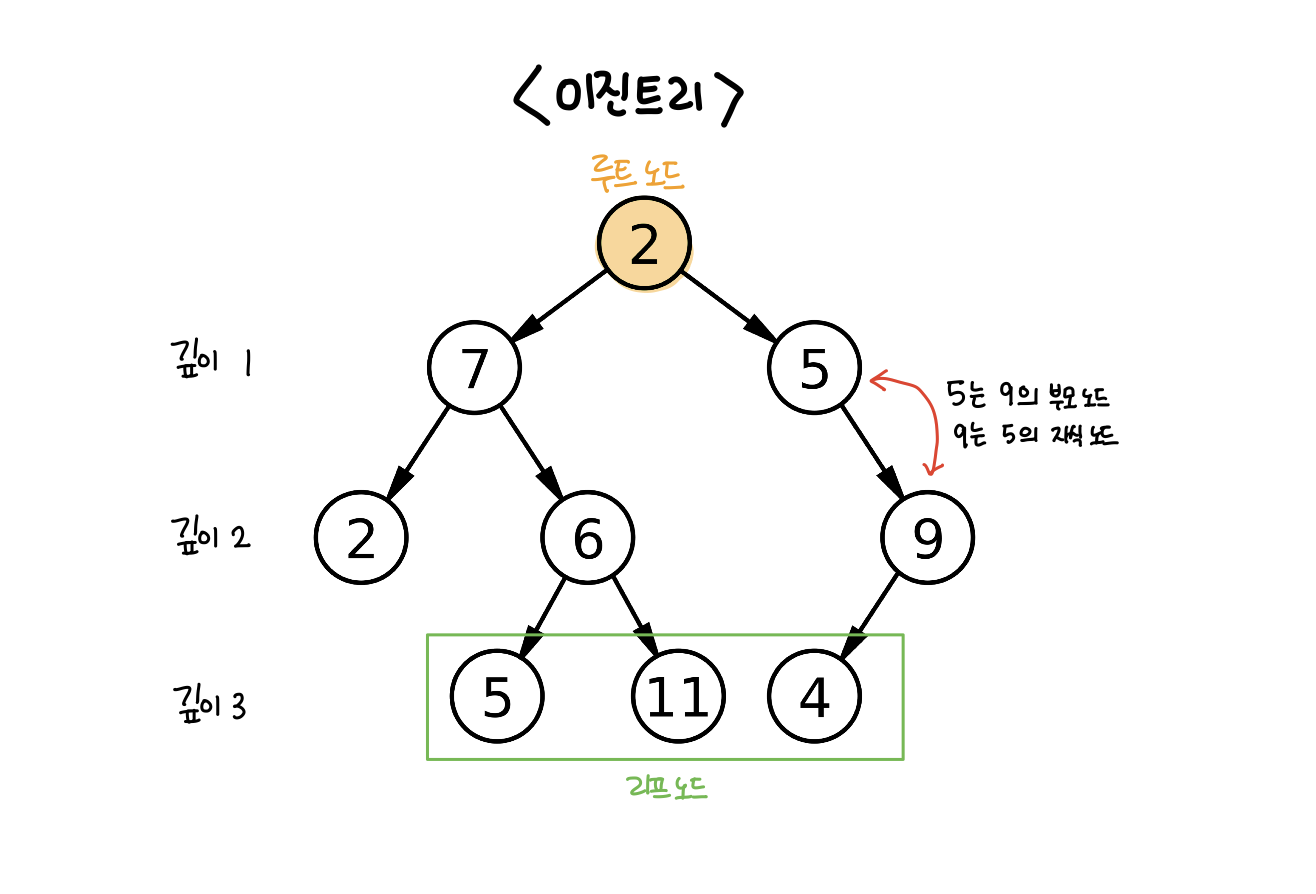
용어 정리
- 루트 노드: 트리에서 다른 어떠한 정점도 가리키지 않는 정점
- 깊이: 루트 노드로부터의 거리
- 리프 노드: 가리키는 정점이 없는 정점들
- 이진 트리: 각 정점들이 자식 노드를 최대 2개까지만 갖는 트리
- 완전 이진 트리: 마지막 깊이를 제외하고 모든 정점이 완전히 채워져 있으며, 마지막 깊이의 정점들은 가능한 한 왼쪽에 있는 트리 (위 그림에서 깊이 3의 노드들이 없으며, 노드 5의 자식 노드가 없다고 가정하면 완전 이진 트리의 모습이 됨)
임의의 정점 A가 다른 정점 B를 가리킬 때
A를 B의 부모 노드라고 하고, B를 A의 자식 노드라고 한다.
구현
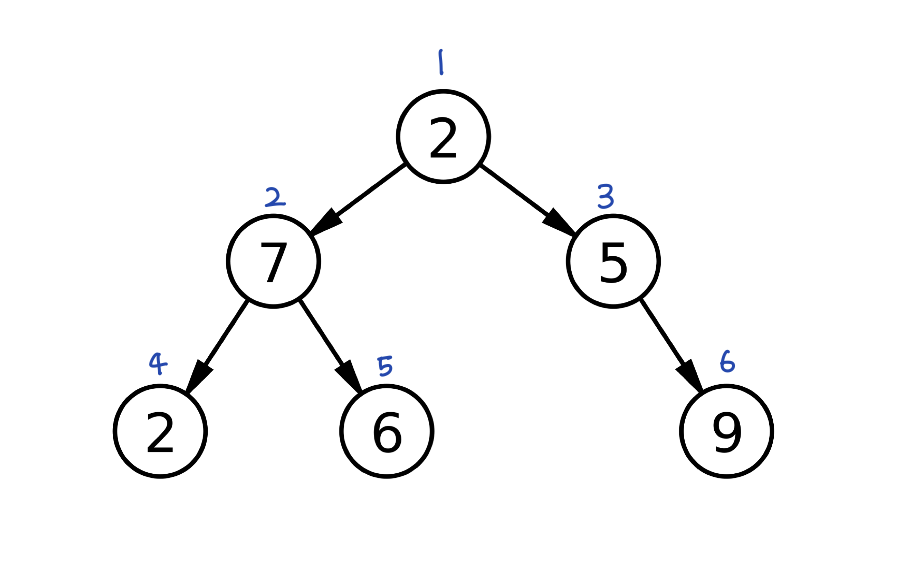
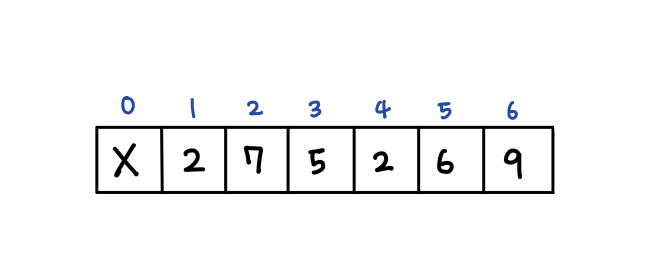
다음과 같이 루트 노드부터 순서대로 번호를 붙인다.
어떤 정점의 번호가 n이면 왼쪽 자식은 2n, 오른쪽 자식은 2n+1 이다.
따라서, 배열로 완전 이진 트리를 표현할 수 있게 된다.
class Tree:
def __init__(self, i, l, r) :
self.index = i
self.left = l
self.right = r
def addNode(self, i, l, r) :
# 트리 내의 정점 i에 대하여 왼쪽자식을 l, 오른쪽 자식을 r로 설정
if self.index == None or self.index == i : #트리가 비어있을 때
self.index = i
self.left = Tree(l, None, None) if l != None else None
# l에 값이 있다면 왼쪽 자식 정점 아래로 트리 생성, 값이 없다면 왼쪽은 None
self.right = Tree(r, None, None) if r != None else None
# r에 값이 있다면 오른쪽 자식 정점 아래로 트리 생성, 값이 없다면 오른쪽은 None
return True # 성공적으로 작동함을 알려주기
else : # 트리가 비어있지 않을 때 -> 재귀적으로 들어가기
flag = False
# flag가 True가 될 때까지 무한대로 탐색한다.
# 왼쪽 노드가 유효하면 왼쪽부터 탐색 시작
if self.left != None :
flag = self.left.addNode(i, l, r)
# 성공하면 flag=True가 되고 addNode 완료
# 왼쪽에서 실패했고, 오른쪽 노드가 유효하다면 오른쪽도 탐색 시작
if flag == False and self.right != None :
flag = self.right.addNode(i, l, r)
# 계속 재귀를 해서 언젠가는 맞는 addNode가 일어나며 트리 생성
return flag트리 순회
비선형 구조인 트리는 자료의 순서가 존재하지 않는다.
트리에 들어있는 자료에 접근하기 위해서는 트리의 모든 노드에 방문하는 순회를 해야 한다.
트리를 순회하는 방법에는 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)가 있다.
✔️ 깊이 우선 탐색(DFS)
DFS는 세 가지 방법이 있으며, 정점을 언제 방문하는지에 따라 순서가 달라지고, 재귀 호출을 이용한다는 기본적인 개념 자체는 동일하다.
(전체 트리를 순회하기 위해 서브 트리를 순회 = 순회를 위한 순회 = 재귀 호출!)
또 재귀 호출은 스택의 특성을 이용하므로 스택을 이용한다고 볼 수 있다.
1. 전위 순회
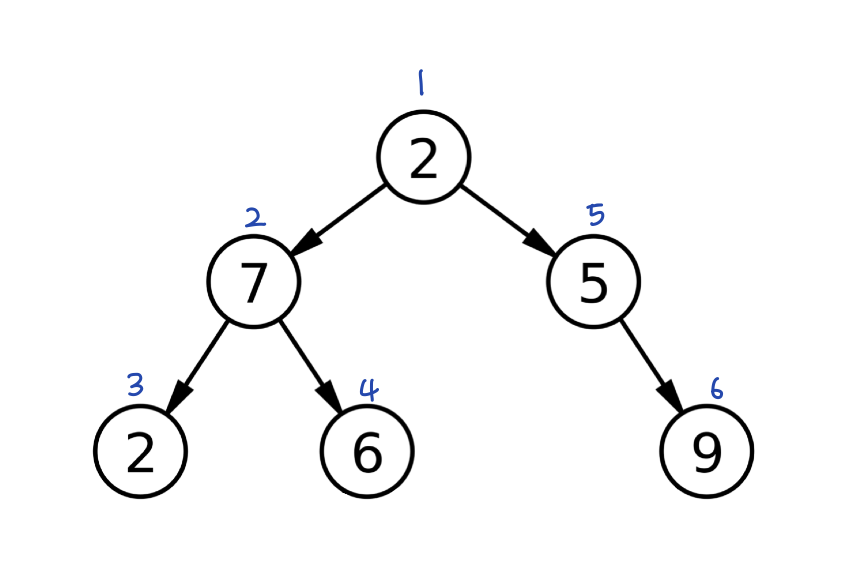
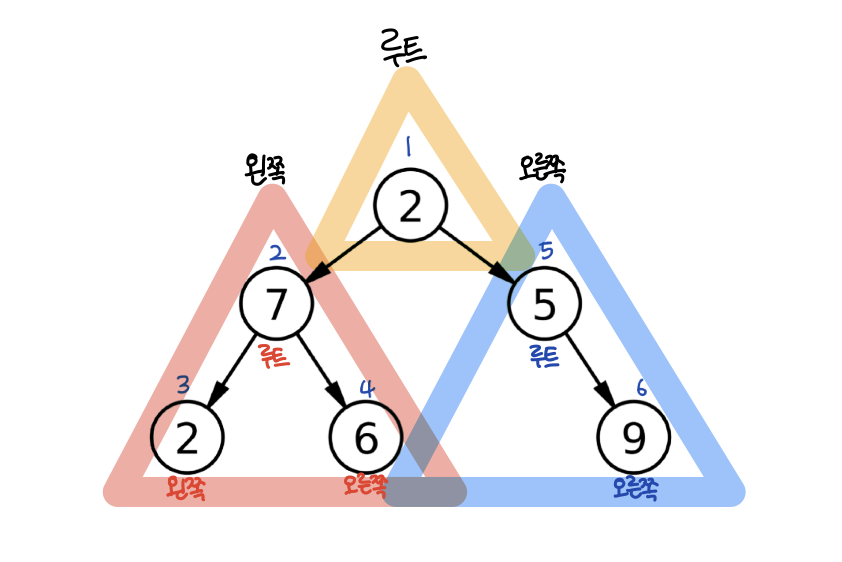
루트 방문 -> 왼쪽 서브트리 순회 -> 오른쪽 서브트리 순회
(자세히 보면 서브트리 안에서도 똑같은 규칙으로 순회한다!)
2. 중위 순회
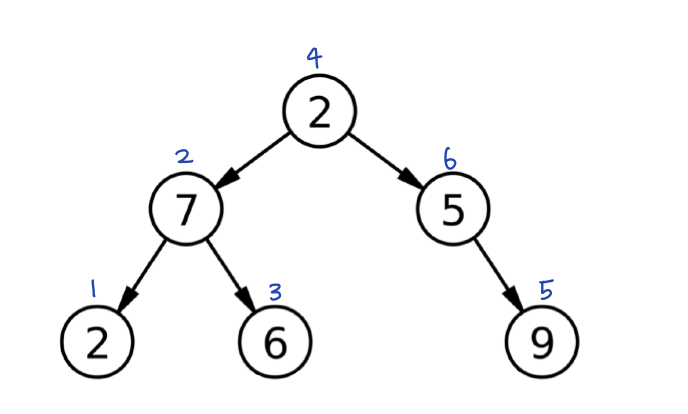
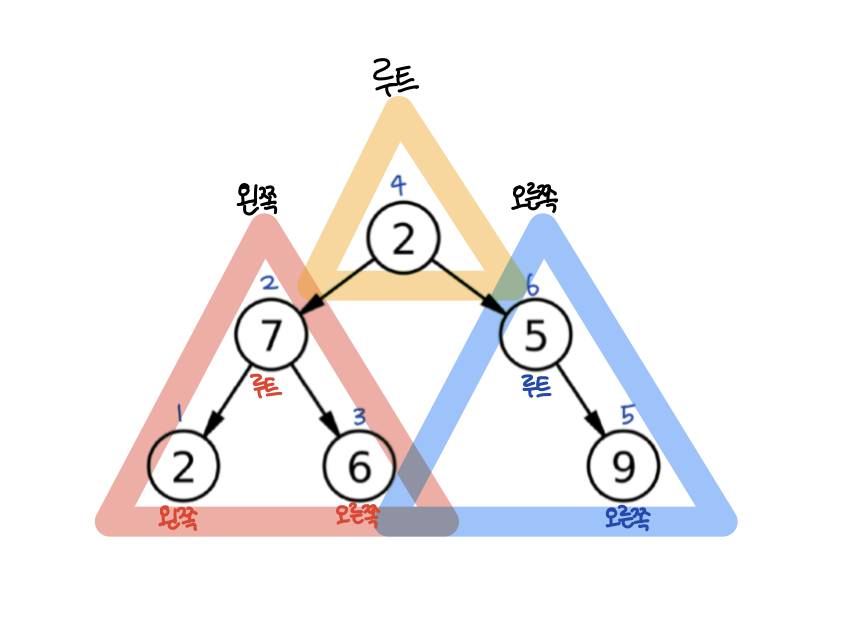
왼쪽 서브트리 순회 -> 루트 방문 -> 오른쪽 서브트리 순회
(자세히 보면 서브트리 안에서도 똑같은 규칙으로 순회한다! 22)
3. 후위 순회
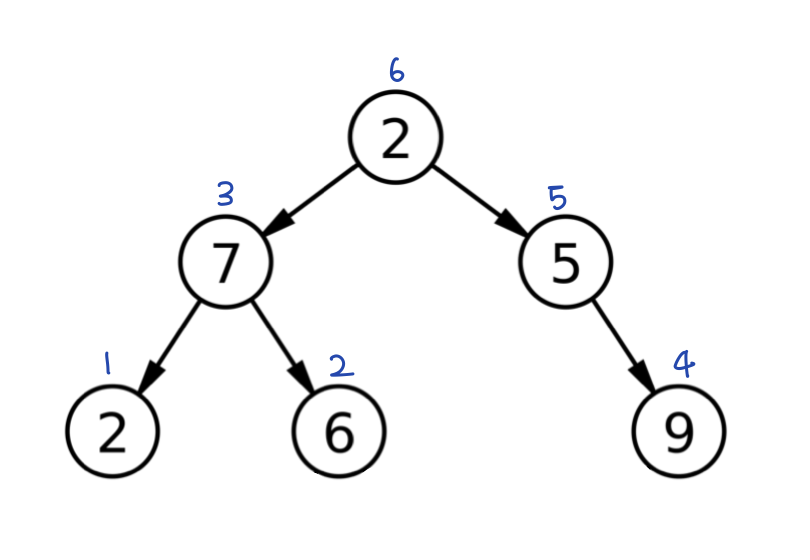
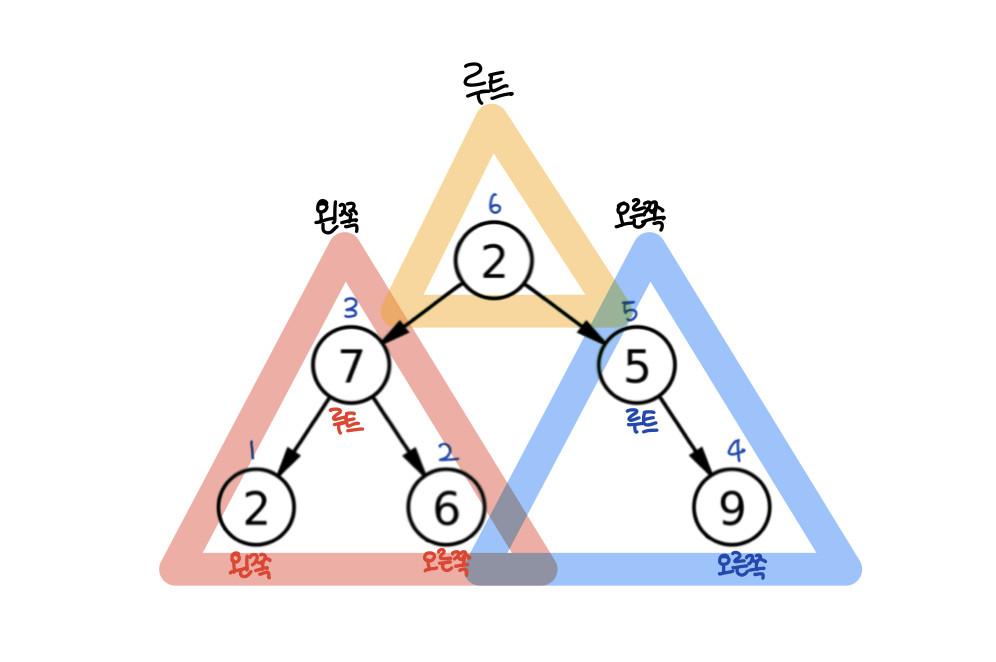
왼쪽 서브트리 순회 -> 오른쪽 서브트리 순회 -> 루트 방문
(자세히 보면 서브트리 안에서도 똑같은 규칙으로 순회한다! 33)
코드 구현
이를 토대로 코드를 구현해보자.
def preorder(tree) : # 전위순회
result = []
result.append(tree.index) # 루트 방문
if tree.left != None: # 왼쪽 서브트리 순회
result += preorder(tree.left)
if tree.right != None: # 오른쪽 서브트리 순회
result += preorder(tree.right)
return result
def inorder(tree) : # 중위순회
result = []
if tree.left != None: # 왼쪽 서브트리 순회
result += inorder(tree.left)
result.append(tree.index) # 루트 방문
if tree.right != None: # 오른쪽 서브트리 순회
result += inorder(tree.right)
return result
def postorder(tree) : # 후위순회
result = []
if tree.left != None: # 왼쪽 서브트리 순회
result += postorder(tree.left)
if tree.right != None: # 오른쪽 서브트리 순회
result += postorder(tree.right)
result.append(tree.index) # 루트 방문
return result
### 사용
from tree import Tree
def main():
'''
첫 번째 줄에 노드의 개수를 나타내는 정수 n이 입력
두 번째 줄부터 n줄에 걸쳐 정수 a b c가 공백으로 구분되어 입력
-> 정점 a가 왼쪽 자식으로 b, 오른쪽 자식으로 c를 갖는다는 의미
만약 노드의 자식 노드가 없다면 -1이 주어진다.
<입력 예시>
5
1 2 3
2 4 5
3 -1 -1
4 -1 -1
5 -1 -1
<출력 예시>
1 2 4 5 3
4 2 5 1 3
4 5 2 3 1
'''
myTree = Tree(None, None, None)
n = int(input())
for i in range(n) :
myList = [int(v) for v in input().split()]
if myList[1] == -1 :
myList[1] = None
if myList[2] == -1 :
myList[2] = None
myTree.addNode(myList[0], myList[1], myList[2])
print(*preorder(myTree))
print(*inorder(myTree))
print(*postorder(myTree))
if __name__ == "__main__":
main()✔️ 너비 우선 탐색(BFS)
BFS는 현재 정점과 이웃한 정점일수록 먼저 방문해야 하므로 FIFO 자료구조인 큐를 이용하여 구현한다.
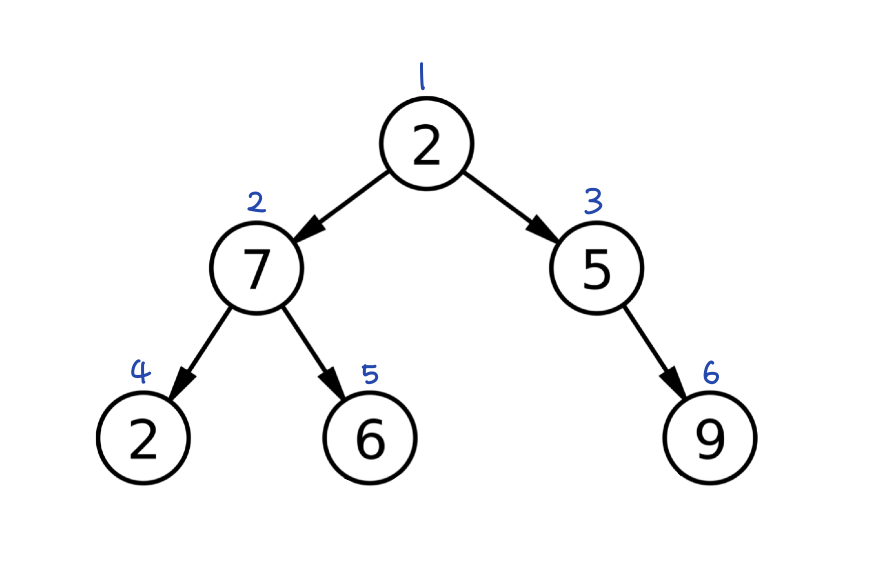
- 루트노드 2에 방문할 때 인접한 노드인 [7, 5]를 큐에 push - [7, 5]
- 노드 7를 pop하며 인접한 노드인 [2, 6]을 큐에 push - [5, 2, 6]
- 노드 5를 pop하며 인접한 노드인 [9]을 큐에 push - [2, 6, 9]
- 큐에 남아있는 노드들을 순서대로 push
코드 구현
from queue import Queue
def BFS(tree) :
q = Queue()
q.put(tree)
result = []
# q에 뭔가 들어있다면(방문할 노드가 남았다면) 계속 반복을 한다.
# = 더이상 방문할 노드가 없을 때 종료한다.
while len(q.queue) > 0:
cur = q.get()
if cur == None:
continue
result.append(cur.index) #방문
q.put(cur.left)
q.put(cur.right)
return result
### 사용
# 사용 코드는 위와 동일
# 출력값은 1 2 3 4 5트리의 사용
컴퓨터에서 트리를 활용하는 예시는 대표적으로 항상 정렬된 상태를 유지하는 자료구조인 이진 탐색 트리가 있다.
이진 탐색 트리에서 어떤 정점의 왼쪽 서브 트리는 그 정점보다 같거나 작은 정점들로만, 오른쪽 서브 트리는 그 정점의 값보다 큰 정점들로만 이루어져 있다.
정렬된 자료구조에서 사용할 수 있는 탐색 알고리즘인 이진 탐색을 이용하면 효율적으로 연산이 가능하다!
시간복잡도
삽입: O(n)
삭제: O(n)
탐색: O(logn)
자세한 내용은 다음 포스팅에서,,,