아직 내가 구현까지 하기엔 조금 어려운 레벨이긴 한 것 같지만
강의를 듣고 머리 속에서 희미해지기 전에 정리해보고자 한다..!

먼저 자료구조 중 트리, 그 중에서도 '이진 트리'에 대해 가볍게 알아보자.

🌲 트리 용어 설명

• 깊이: 루트 노드에서 해당 노드까지 도달하는데 사용하는 간선의 개수 (깊이-간선)
• 높이: 루트 노드에서 해당 노드까지 도달하는데 지나간 노드의 개수 (높이-노드)
• 내부 노드: 자식이 있는 노드
• 외부 노드(=단말 노드, leaf): 자식이 없는 노드 (트리의 맨 끝 라인)
• 노드의 차수: 노드의 자식 수
• 트리의 차수: 해당 트리에 있는 모든 노드의 차수 중 최댓값

🌲 이진 트리: 트리의 자식 수가 2 이하(0, 1, 2)인 트리

• 높이가 N인 이진 트리의 최대 노드 개수는 2^N-1개 이다.

정 이진 트리

• 모든 노드의 차수가 0 또는 2인 이진 트리

포화 이진 트리

• 정 이진 트리에서 모든 단말 노드의 깊이가 같은 이진 트리 (완벽한 삼각형 모양)
• 높이가 H인 포화 이진 트리의 노드 개수는 2^H-1개 이다.
• 깊이가 D인 포화 이진 트리의 단말 노드(leaf) 개수는 2^D개 이다.
  -> 인덱스 트리(indexed tree)에서 사용

완전 이진 트리

• 노드가 왼쪽에 몰려있고 마지막 레벨을 제외하면 포화 이진 트리의 구조를 가진 이진 트리
  -> 힙(heap)에서 사용

🌲 이진 트리의 표현

• 일차원 배열을 이용(0번 인덱스는 비워두고, N+1개)
• 배열에 트리 노드를 레벨 순, 왼쪽에서 오른쪽으로 저장한다.
  이진 트리에서 부모 노드의 왼쪽 자식은 부모노드*2 (=항상 짝수),
  오른쪽 자식은 부모노드*2+1 (=항상 홀수)
  자식의 부모 노드는 자식/2

가볍게 라고 한것치곤 꽤나 길어졌지만 ㅎㅎㅎ..
이것까지 기억해야 인덱스 트리에 접근할 수 있기 때문에 정리해보았다!

인덱스 트리 (Indexed Tree)

만약, 어떤 배열의 구간 합을 구하는 문제가 주어진다면 배열의 누적합을 구해 필요한 만큼만 빼 주는 방법으로 간단하게 구할 수 있을 것이며 그 때의 시간복잡도는 O(N)일 것이다.
그런데 중간에 배열의 어떤 값이 바뀐다면, 누적합 방법을 사용할 수 없다.
이럴 때 인덱스 트리를 사용하면 아주 좋다.
시간복잡도는 아래에서 더 자세히 다루겠지만 O(MlogN)이다!

• 인덱스 트리: 포화 이진트리 형태의 자료구조
• 각 노드는 다음과 같은 의미를 가진다.
  1. 리프 노드: 배열에 적혀있는 수
  2. 내부 노드: 왼쪽 자식과 오른쪽 자식의 합
• 리프 노드의 개수가 N개 이상인 포화 이진트리는 높이가 최소 logN이다.
• 리프 노드의 개수가 N개보다 많아 비어있는 공간이 발생할 경우 구조에 지장이 가지 않게 초기값을 설정한다. (ex: 합을 구할 경우 초기값을 0으로 준다)
  
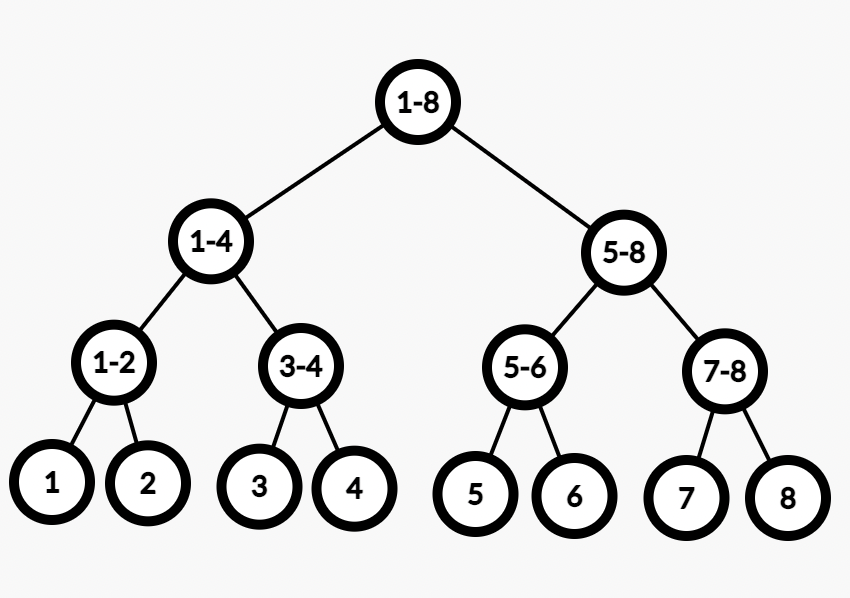
  각 노드에 적혀있는 값은 a~b까지의 합을 뜻한다.

인덱스 트리 또한 배열로 표현하는데, 배열에서는 1~8이 인덱스를 뜻하고, 각 구역의 합이 데이터로 들어가서 [3, 2, 4, 5, 1, 6, 2, 7]의 형태가 된다. (형식상 설명으로 인덱스 0은 뺐다)
트리에는 적혀있지 않지만 1-2는 1구역~2구역의 합인 5, 3-4에는 9, 1-4에는 14... 와 같은 식으로 담겨있다.
(합의 값은 트리 만드는 프로그램의 특성 상 적지 못했다... 좀 기울어져있어도 넘어가도록 하자 프로그램 만지다가 홧병날뻔 ㅂㄷㅂㄷ)
leaf는 무조건 2의 거듭제곱 형태로만 가능하며, 지금은 데이터가 8개라 leaf도 8개지만 만약 9개였다면 16개의 배열을 생성해야 한다.
그렇다면 배열에는 리프 노드에 대한 정보만 담겨 있는건데, 내부 노드까지 구현하려면 어떻게 해야할까?
Top-Down 방식과 Bottom-Up 방식 두 가지가 있다.
다시 한번 말하지만 누적합 중 값이 변경되는 문제에 사용하기 좋은 방법이다! 자신 노드의 자신의 합이 포함된 부모 노드의 값만 변경해주면 되기 때문에 빠르다.

공통점

• S: leaf의 시작점이자 leaf의 사이즈를 뜻한다. 2의 제곱수로 항상 짝수이다.
  S를 통해 많은 것을 알 수 있는데, 이를테면 내부 노드의 마지막 인덱스는 S-1이고, 노드의 총 개수는 S+(S-1) = 2S-1 이다. (배열은 0을 비워주므로 2S)
  또 leaf node에서 i번째 데이터의 인덱스는 S+i-1 이다.
• N: leaf에 있는 노드의 총 개수이다. S와 다를 수 있으니 개념 혼동에 주의하자.

차이점은 두 가지 방식을 살펴본 후 서술하려 한다.

Top-Down 방식

특징

• DFS 기반의 트리 탐색 (재귀 호출)
• 가지치기 가능: 내려가다가 쓸모없는 데이터임을 확인하면 손절 가능
• Top-Down으로만 해결 가능한 문제들이 있음 (x번째로 빠른 수 등 카운팅 쿼리 문제)

Init(left, right, node)

• 배열에 값을 넣는 과정
  
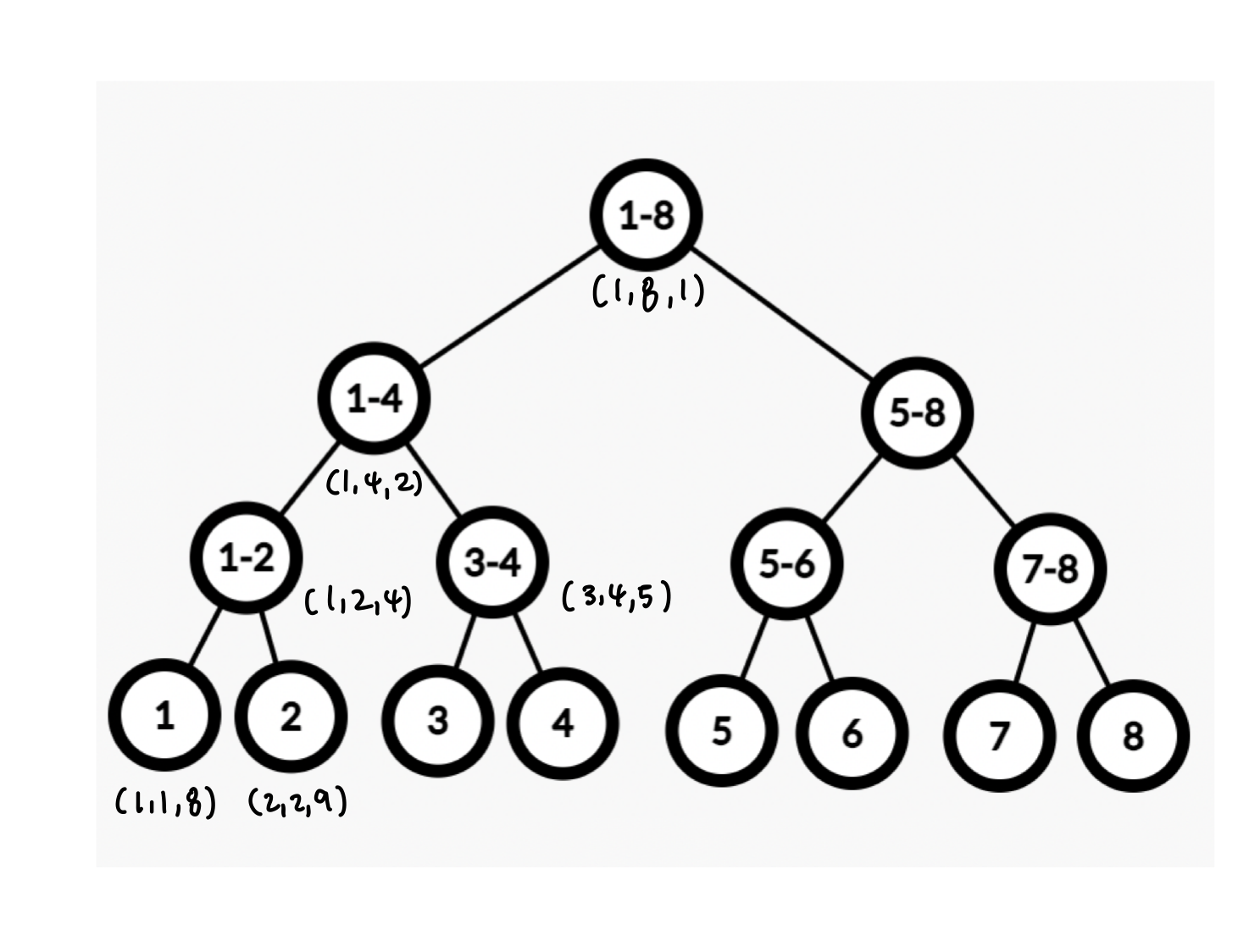
• Root부터 시작: init(1, 8, 1) 여기서 8은 N이 아닌 S!
• 내부 노드일 경우 (if left != right): leaf만 left==right. 개인의 합만 갖고 있음
  - 왼쪽 자식 init(left, mid, node*2) 호출
  - 오른쪽 자식 (mid+1, right, node*2 + 1) 호출
  - 왼쪽 + 오른쪽 자식 값 합쳐서 노드에 저장
  - 노드의 값 리턴
• 리프 노드일 경우 (if left == right)
  - 노드에 배열의 값 저장
  - 노드의 값 리턴

Query(left, right, node, queryLeft, queryRight)

• 부분합을 구하는 과정
• 쿼리는 세가지 경우로 나눌 수 있다.
  - 연관 없음
  - 판단 가능
  - 판단 불가

ex) 인덱스 3~7의 부분합을 구하고 싶은 경우

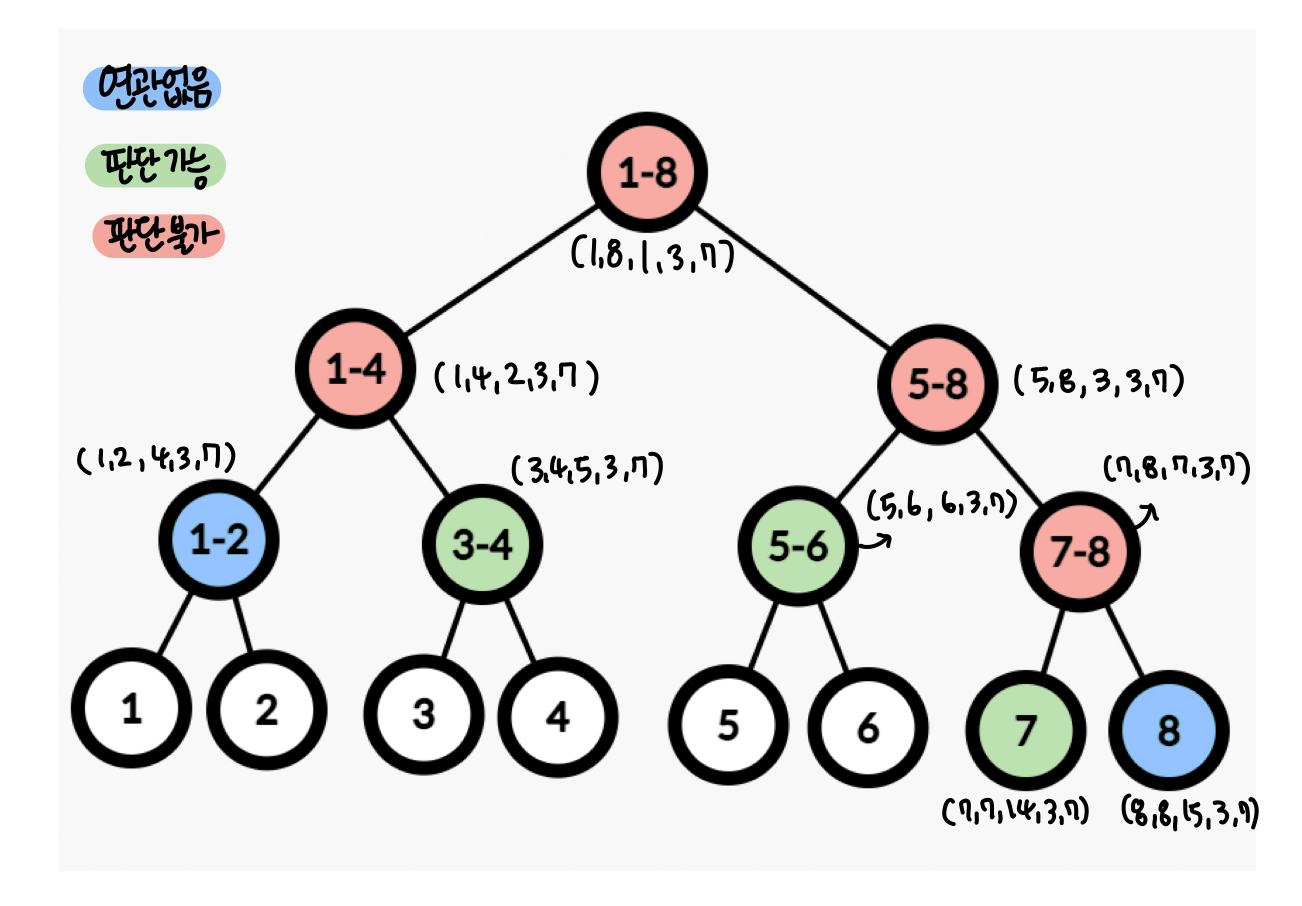
• Root부터 시작: query(1, 8, 1, 3, 7)
• 노드가 쿼리 범위 밖: 연관 없음 -> 무시
• 노드가 쿼리 범위 안에 들어옴: 판단 가능 -> 현재 노드의 값 리턴
• 노드가 쿼리 범위에 걸쳐있음: 판단 불가
  - 왼쪽 쿼리(1, mid, node*2, 3, 7)를 호출
  - 오른쪽 쿼리 (mid+1, r, node*2+1, 3, 7)을 호출
  - 왼쪽 + 오른쪽 쿼리 값을 합쳐서 리턴
  

Update(left, right, node, target, diff)

• leaf 노드의 값을 갱신하는 과정

ex) leaf 노드의 3번째 값을 4->2로 변경하고 싶은 경우

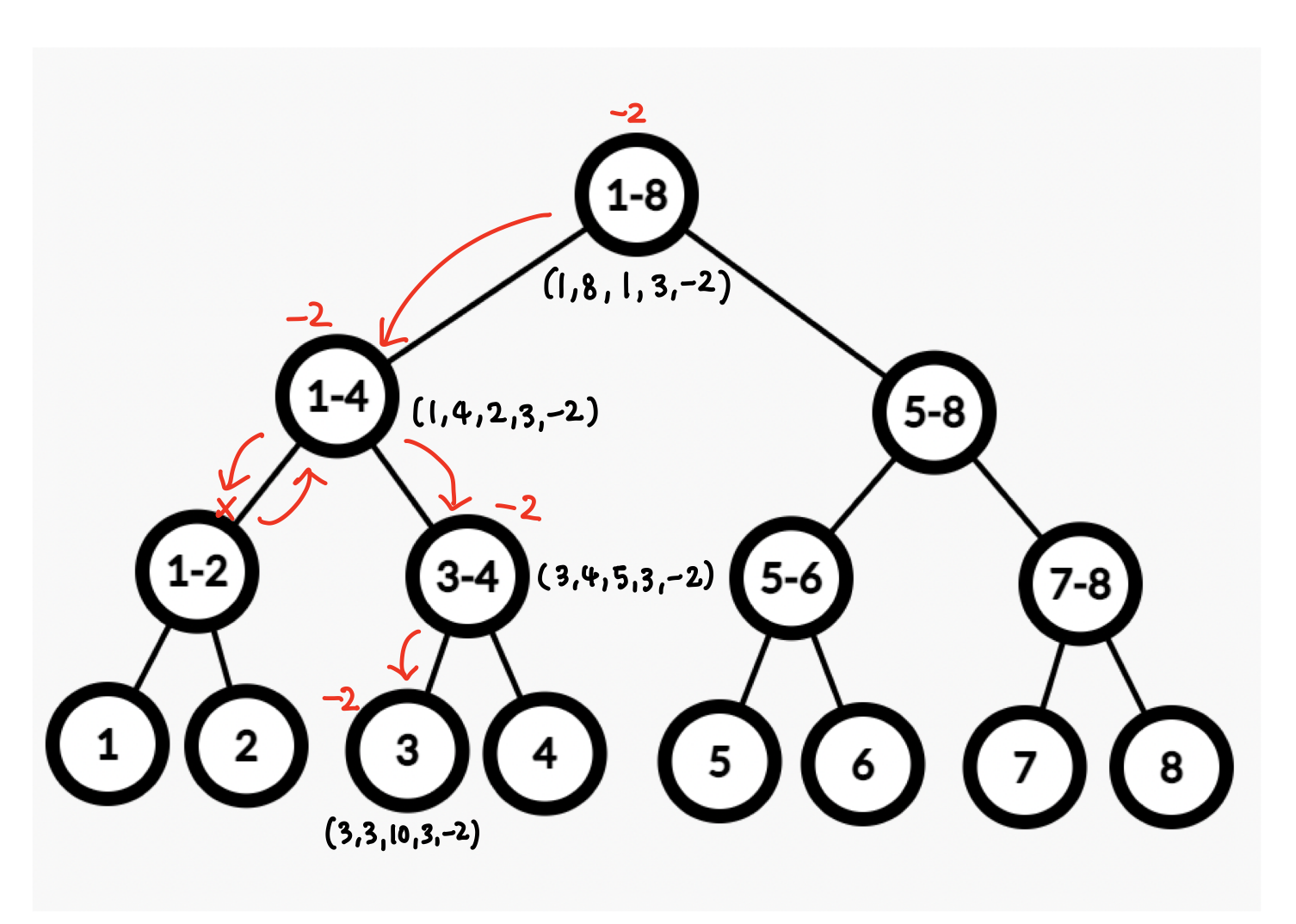
• S=8이므로 배열에서 A[S+3-1] = A[3] = 4 임을 알 수 있고,

• diff는 변경값-원래값 = 2 - 4 = -2이다.

• value가 아닌 diff를 이용해야 leaf로 내려가는 과정에서 변경하려는 노드와 관련된 노드들의 값도 변경할 수 있다!

• 노드가 target 미포함: 연관 없음 -> 무시

• 노드가 target 포함: 현재 노드에 diff 반영
  - 자식이 있을 경우

  • 왼쪽 update(l, mid, node*2, 3, -2)
  • 오른쪽 update(mid+1, r, node*2+1, 3, -2)

Bottom-Up 방식

특징

• 반복문 기반 이동
• index의 홀짝 특성을 이용함: S, 왼쪽 노드는 짝수 / 오른쪽 노드는 홀수
• 부모 = 노드/2 이용
• 코드가 단순하며 수행속도가 미세하게 빠름

Init

• leaf부터 순회: [S] ~ [S+N-1] 순회하며 노드에 배열의 값 저장 (배열에 8번부터 15번까지 저장됨)
• 내부노드 순회: leaf 순회가 끝나면 [S-1] ~ [1]까지 1씩 감소하며 순회 (배열에 7번부터 1번까지 감소하며 저장됨)
  - 왼쪽 자식: index*2
  - 오른쪽 자식: index*2 + 1
  - 왼쪽 + 오른쪽 자식 값을 합쳐서 노드에 저장
  

Query(queryLeft, queryRight)

ex) 인덱스 3~7의 부분합을 구하고 싶은 경우

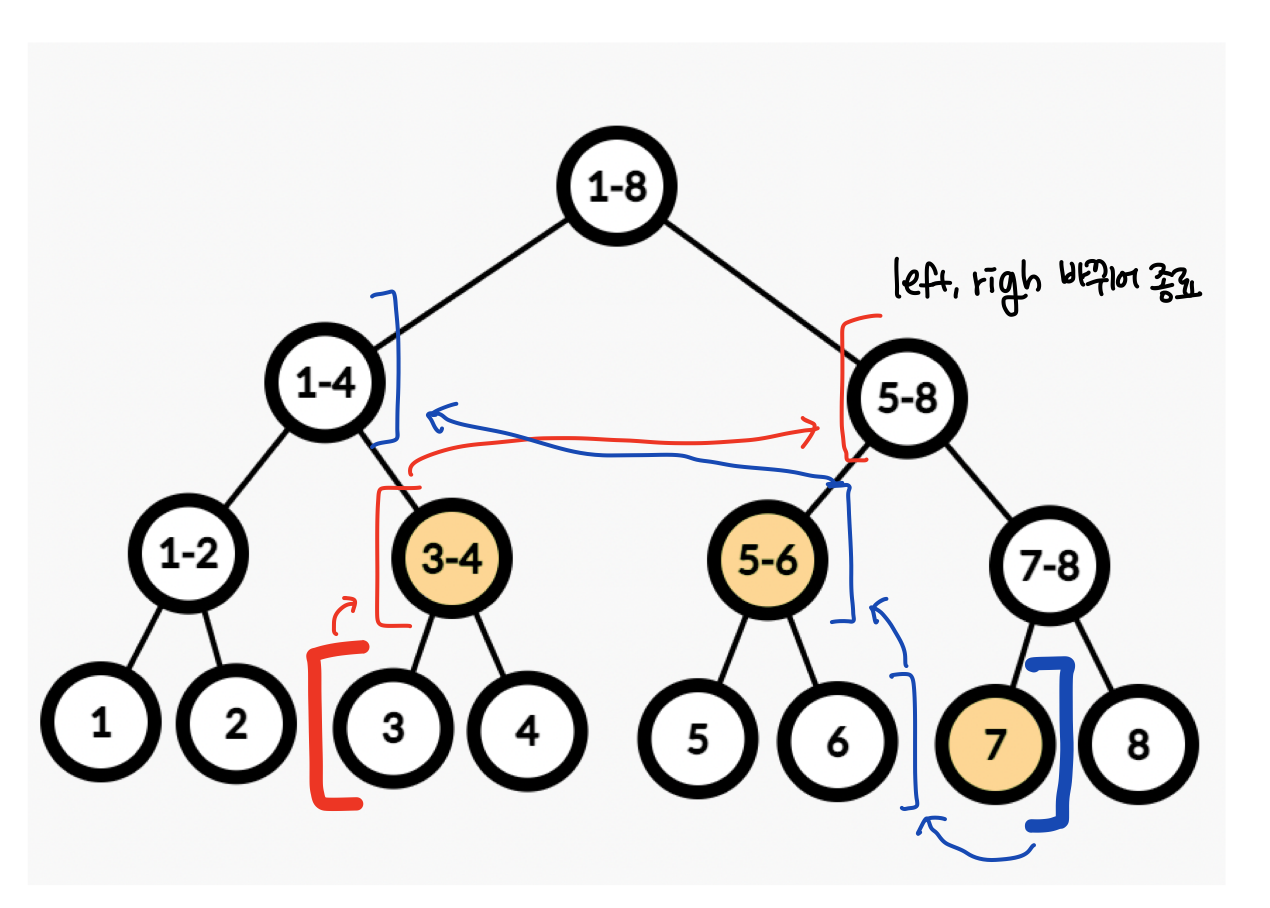
• leaf 노드부터 시작: query(3,7)
  - nodeLeft = S + queryLeft - 1
  - nodeRight = S + queryRight - 1
• while (nodeLeft <= nodeRight): 왼쪽과 오른쪽 부분합 구간이 뒤바뀌면 반복 종료
• leftNode 분기 조건
  - 짝수일 경우, 좌우 노드 모드 포함되므로 부모 값 사용 가능 -> leftNode = leftNode / 2로 leftNode 이동
  - 홀수일 경우, 부모 값을 사용할 수 없고 본인 노드만 사용 가능 -> 현재 노드 값 추가 -> leftNode = (leftNode + 1) / 2로 leftNode 이동
• rightNode 분기 조건
  - 짝수일 경우, 부모 값을 사용할 수 없고 본인 노드만 사용 가능 -> 현재 노드 값 추가 -> rightNode = (rightNode - 1) / 2 로 rightNode 이동
  - 홀수일 경우, 좌우 노드 모드 포함되므로 부모 값 사용 가능 -> rightNode = rightNode / 2 로 rightNode 이동
  

Update(target, value)

ex) leaf 노드의 3번째 값을 4->2로 변경하고 싶은 경우

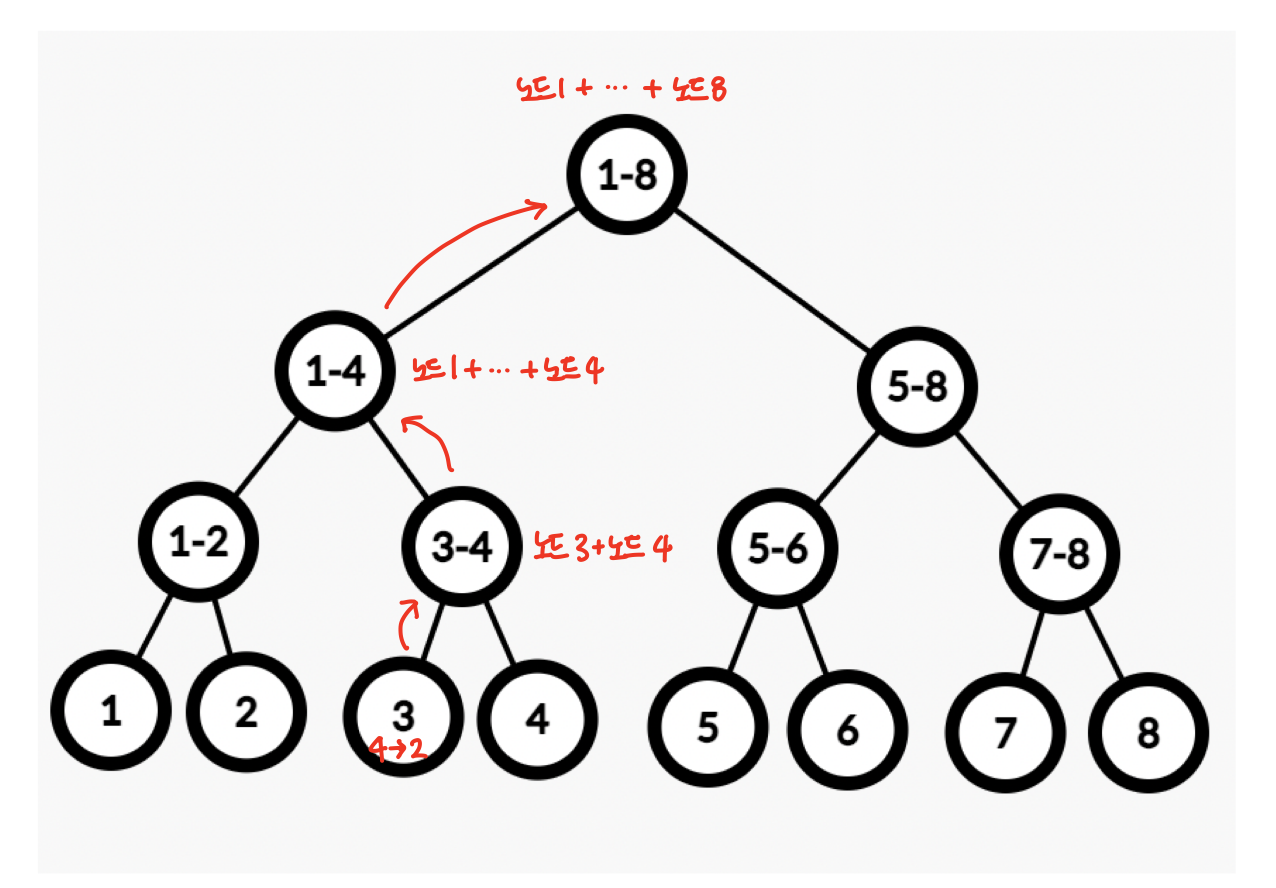
• value 대신 diff 써도 가능
• node = S + target - 1 로 바로 leaf에 접근 가능
• leaf 노드부터 시작: update(3, 2)
• 노드를 해당 값으로 갱신
• 부모로 이동: node / 2
• while (node >= 1): root에 도달할 때까지 반복
  - 좌측(node*2)과 우측(node*2 + 1) 합을 노드에 저장
  - 부모로 이동: node / 2
  

차이점

• 어떤 범위를 통으로 갱신하는 경우 bottom-up 방식이 편하다.
• 하지만 bottom-up은 전체를 순회해야 한다.
  -> 0, 1로 이루어진 데이터의 경우 top-down 방식이 유리하다.

끝으로

오늘 강의를 들으며 많이 벅차고 힘들었는데 3시간 가까이 글을 작성하며 어느 정도 정리된 것 같다. 역시 블로그 포스팅은 시간이 많이 들지만 이해에는 직빵이다... 라는 생각을 하며 간만의 포스팅을 마친다.
다음 포스팅은 시간복잡도, DFS/BFS 에 대해 다루고 싶은데 주말에 쓸 수... 있겠지...? ^^
아무튼 끝!