합승 택시 요금
[문제]
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.
[제한사항]
- 지점갯수 n은 3 이상 200 이하인 자연수입니다.
- 지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 즉, 출발지점, A의 도착지점, B의 도착지점은 서로 겹치지 않습니다.
- fares는 2차원 정수 배열입니다.
- fares 배열의 크기는 2 이상 n x (n-1) / 2 이하입니다.
- 예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (6 x 5 / 2 = 15)
fares 배열의 각 행은 [c, d, f] 형태입니다.- c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
- 지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 요금 f는 1 이상 100,000 이하인 자연수입니다.
- fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, [c, d, f]가 있다면 [d, c, f]는 주어지지 않습니다.
- 출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.
[입출력 예]
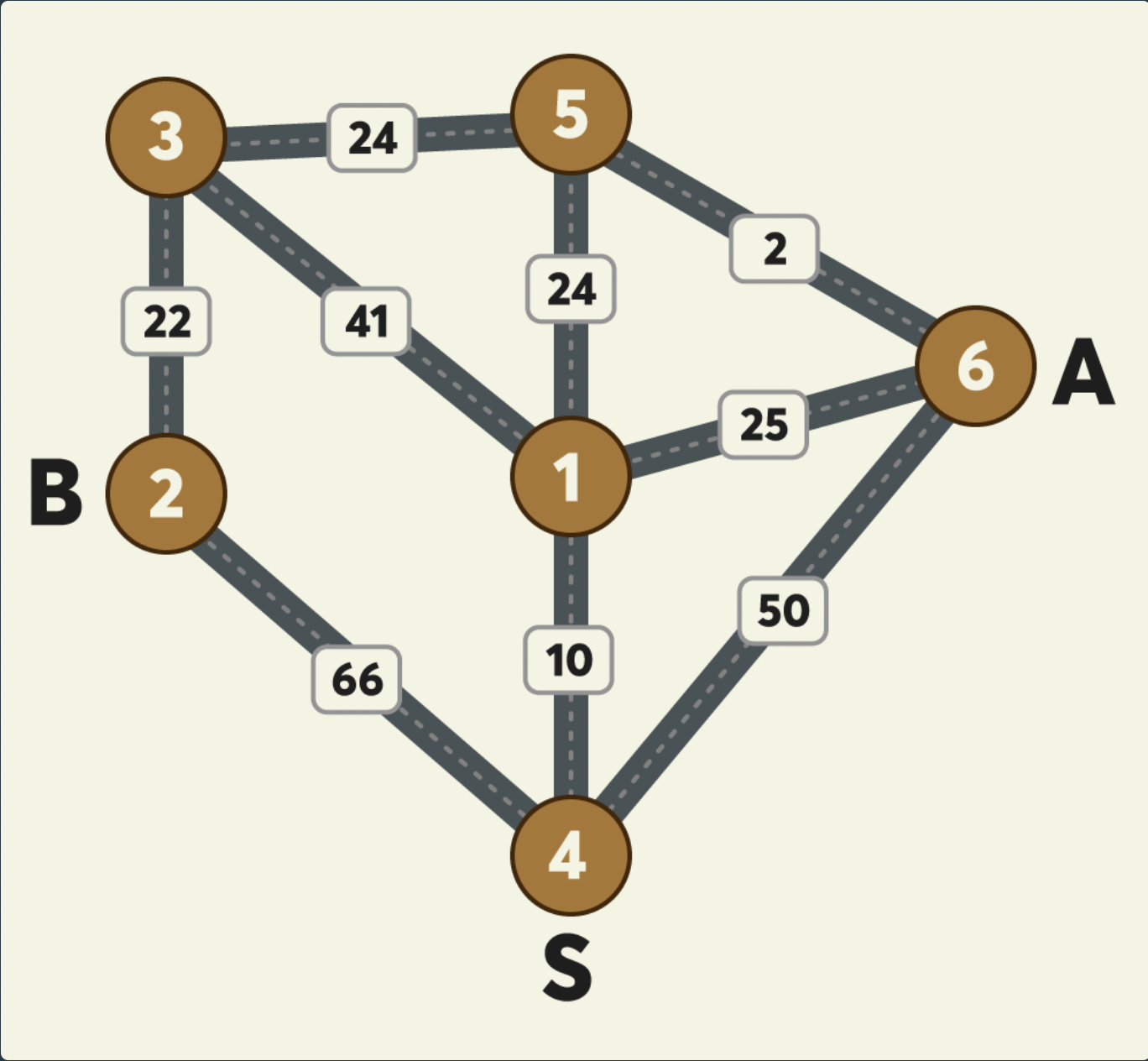
n s a b fares result 6 4 6 2 [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]] 82 7 3 4 1 [[5, 7, 9], [4, 6, 4], [3, 6, 1], [3, 2, 3], [2, 1, 6]] 14 6 4 5 6 [[2,6,6], [6,3,7], [4,6,7], [6,5,11], [2,5,12], [5,3,20], [2,4,8], [4,3,9]] 18
concept
- 어느 구간에서 합승을 해야할 지 골라야 한다.(floyd warshall)
- 각각의 합승 구간에서 도착 지점까지 최소경로로 이동해야 한다. (floyd warshall을 이용하여 각각의 경로를 거쳐 가는 최소 비용을 미리 구해놓기)
- 그래프의 정보를 간선의 정보로 저장x -> floydwarshall은 그래프로 표현하는 것이 편함
- 완전탐색
Code
INF = 987654321
def solution(n, s, a, b, fares):
answer = INF
#그래프 선언 -> 최소비용을 구해야하므로 INF로 설정후 갱신
graph = [[INF for _ in range(n+1)] for _ in range(n+1)]
#0번째 노드는 사실상 필요 없음.
for i in range(1, n+1):
graph[i][i] = 0
#양방향 그래프
for fare in fares:
graph[fare[0]][fare[1]] = graph[fare[1]][fare[0]] = fare[2]
#floyd warshall
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])
#경유지 (k까지 같이 갔다가 최소비용으로 각자의 목적지로 이동)
for k in range(1,n+1):
answer = min(answer, graph[s][k]+graph[k][a]+graph[k][b])
return answer참고
- floyd warshall 시작점과 도착점의 최소 비용을 구하는 알고리즘.
- 어찌보면 하나의 경로만 거쳐 지나가는 최소비용을 구하는 것처럼 보이지만,, 잘 생각해보면
ex) 1->2->3->4의 이동 경로 1->4로의 최소 비용이라면, 1->3으로 도착하는 경로의 최솟값은 1->2->3으로 설정될 것이다.. - 다익스트라로도 구현해볼것 나중에..^^
- 만약, 최소한의 이동경로를 구하라고 한다면..?
