📌 활성함수
- 신경망: 선형모델 + 활성함수
- 비선형함수 => nonlinear로 변형
- 선형모델의 잠재벡터 z에 개별적으로 적용하여 새로운 잠재벡터 H를 만든다.
- 활성함수가 없으면 딥러닝은 선형모델과 차이가 없다.
1. Sigmoid 함수
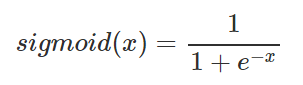
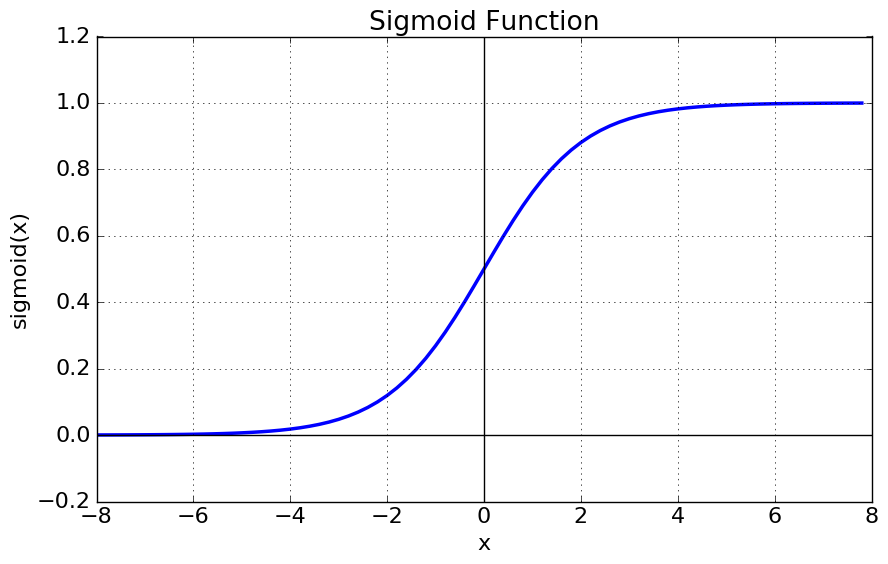
- = Logistic 함수
- 함수값이 [0,1] 로 제한된다
- 중심값이 0.5 이다
- Vanishing Gradient 문제
2. Hyperbolic Tangent (tanh)
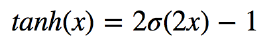
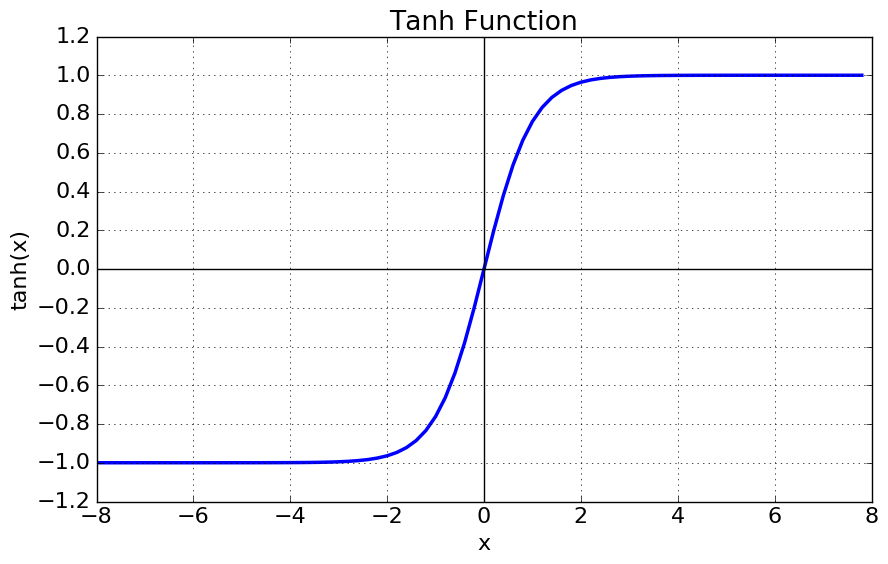
- 함수값이 [-1,1] 로 제한된다
- 중심값이 0 이다
- Vanishing Gradient 문제
Sigmoid와 tanh의 Vanishing Gradient 문제
Sigmoid의 미분
-
전개
-
Sigmoid의 도함수 그래프
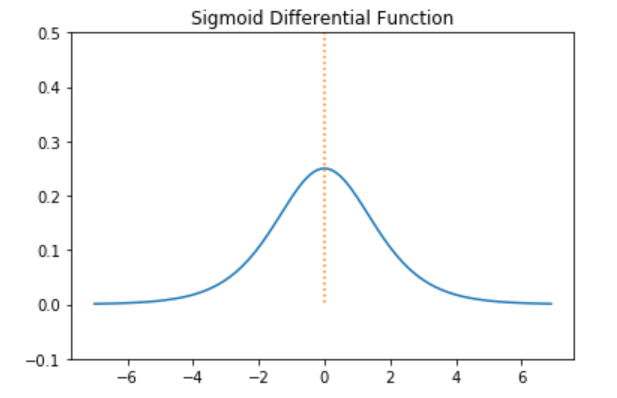
-
Sigmoid 미분값 범위 : (0, 0.25]
tanh의 미분
-
전개
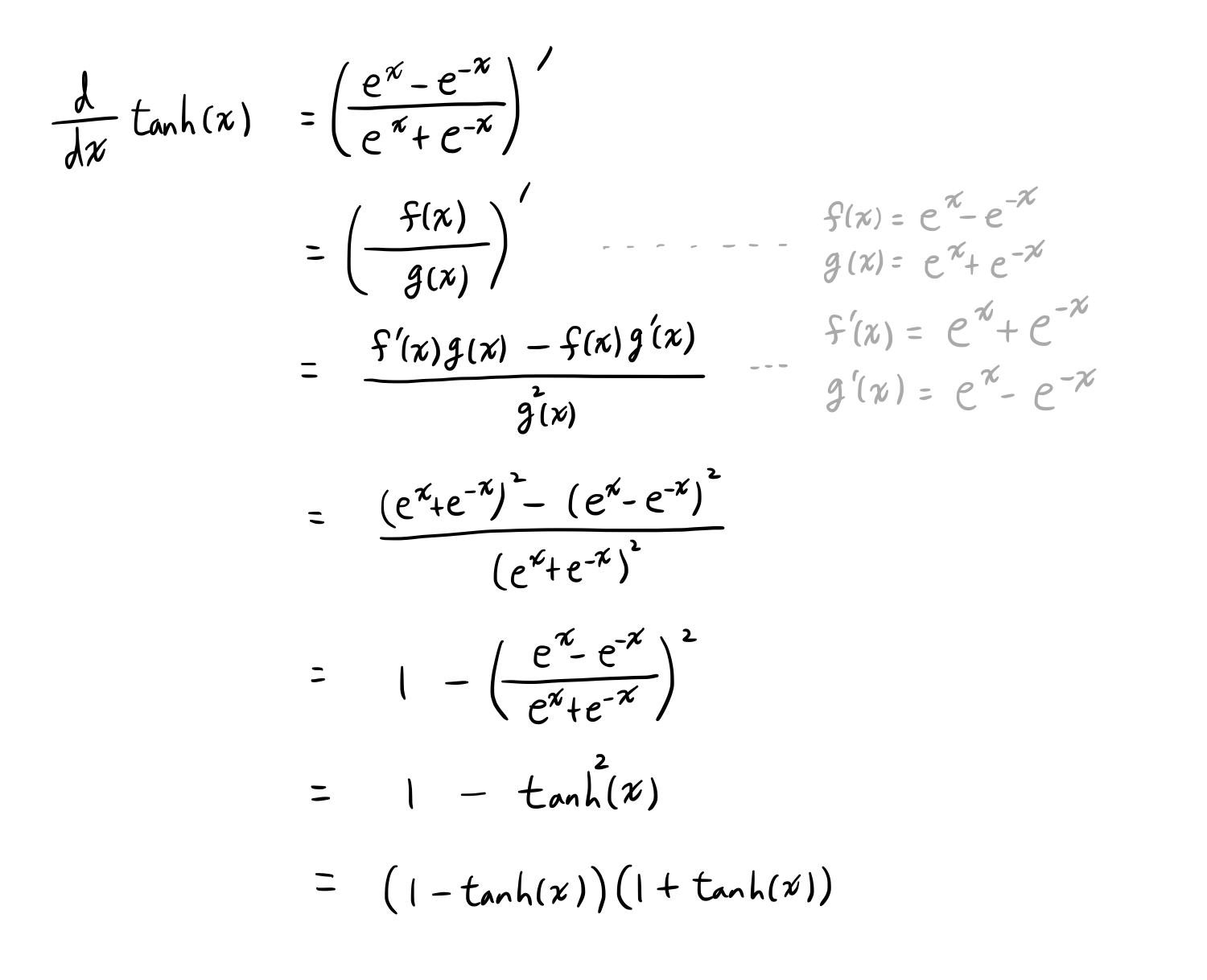
-
tanh의 도함수 그래프
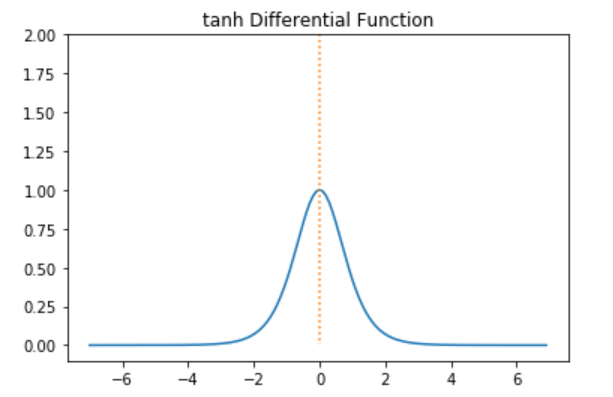
-
tanh의 미분값 범위 : (0, 1]
back propagation 과정에서 연쇄적으로 활성화함수의 미분값을 곱해야 하는데, Sigmoid와 tanh은 미분 최대값이 작기 때문에 층이 깊을수록 값이 작아져 최소까지 업데이트할 수 없는 문제가 발생한다. 이를 기울기 소실, Vanishing Gradient라고 한다.
이 문제를 ReLU 활성화함수를 통해 해결할 수 있다.
3. Rectified Linear Unit (ReLU)
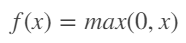
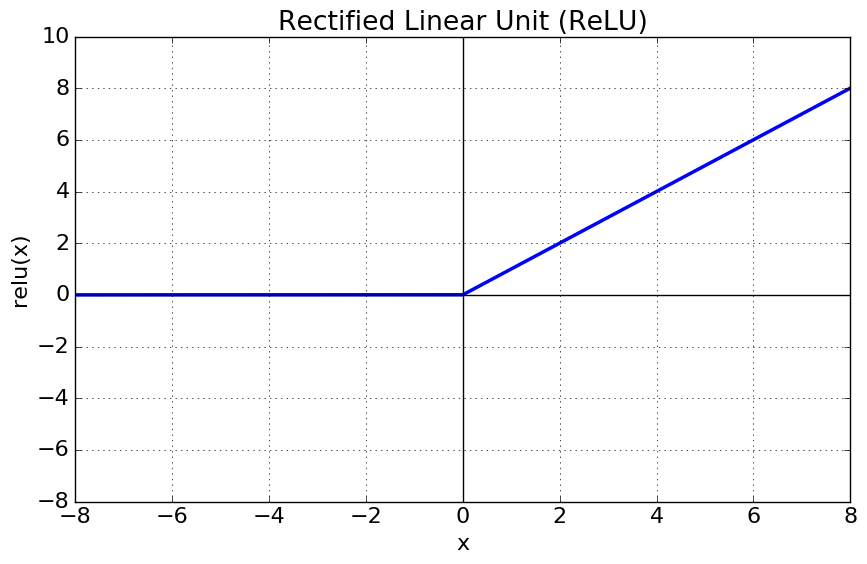
- x > 0 : 기울기 1인 직선, x < 0 : 값 0
- Sigmoid, tanh에 비해 연산이 빠르다
- Sigmoid, tanh에 비해 Gradient가 출력층과 멀리 있는 Layer까지 전달할 수 있다
- 특정 범위에서 neuron 이 죽게 된다
- 선형이 아닌 비선형
- 양 극단값이 포화되지 않음
ReLU의 미분
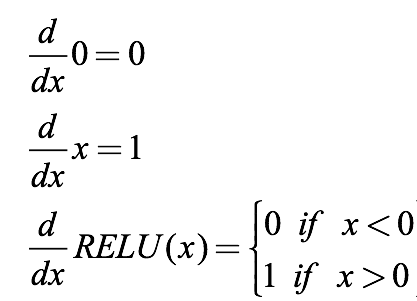
- ReLU의 도함수 그래프
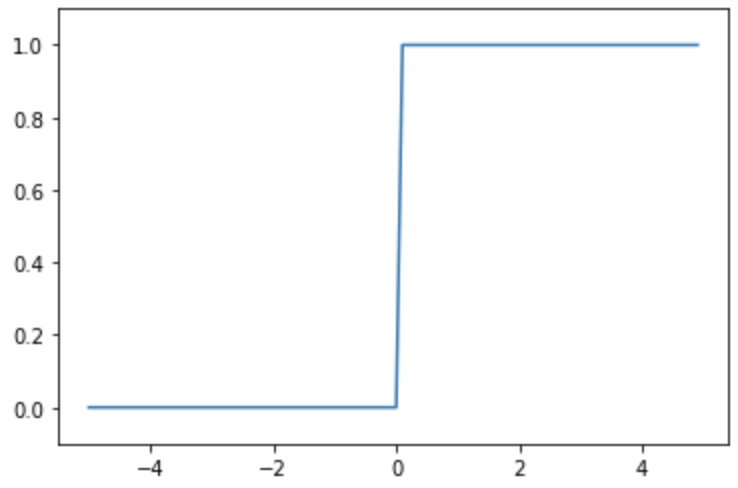
다음엔 Leaky ReLU를 다룰 것.


Vanishing Gradient 는 딥러닝 학습에서 자주 나오는 문제입니다.
수식으로 이를 설명하는 방법에 대해서 알아두면 더 좋을 것 같습니다!
추가로 Dead ReLU 문제와 Leaky ReLU도 더 공부해보세요!