1. Finality (완결성)

블록체인에서 블록이 한번 포함되고 나면 되돌릴 수 없음을 의미한다.

• 확률적 finality
  블록을 되돌릴 수 없다는 것을 확률적으로만 보장한다. 비트코인의 합의 알고리즘이 사용하는 방식으로 블록이 추가로 생성될 수록 앞쪽에 있는 블록의 finality가 증가하는 방식이다. 거래소에 비트코인을 입금하면 6개의 블록 컨펌을 기다린 이후 거래가 가능한 이유는 거래소에서 확률적으로 finality를 체크하기 때문이다.

• 절대적 finality
  블록이 한 번 블록체인에 포함되면 어떤 경우에도 해당 블록을 되돌릴 수 없음을 보장하는 방식이다. 텐더민트와 같은 BFT 계열의 합의 알고리즘이 절대적 finality를 보장한다.

두 가지 finality의 성격만 보았을 때는 절대적 finality가 무조건 좋아보이지만, 사실 여기에는 트레이드오프 관계가 있다. 절대적 finality는 쉽게 얻어지지 않는다. 이 문제에 대해 Eric Brewer의 CAP 정리를 함께 살펴볼 필요가 있다.

1-1. CAP 이론

CAP 이론은 인터넷을 통해 서비스를 제공하고 싶다면 서비스 제공자가 보장해야 할 3가지 특성에 대한 것이다.

일관성 (Consistency)

사용자는 항상 최신 정보를 서비스 받는 것을 보장한다. 모든 사용자는 항상 동일한 데이터를 조회한다.

한 노드에서 특정 데이터의 처리가 완료되었을 때 다른 노드가 동시다발적으로 업데이트된 정보에 접근할 수 있어야 한다.

가용성 (Availability)

서비스가 중단되지 않음을 보장한다. 일부 노드가 중단되어도 다른 노드들에게 영향을 주지 않아야 한다.

오류가 없는 노드가 발송한 메시지는 오류가 없는 모든 노드로부터 응답받을 수 있어야 한다. 또한 데이터 저장소에 대한 모든 동작이 오류가 없는 모든 노드로부터 성공적으로 리턴을 받아야 한다.

CAP 이론에서 가용성은 응답 시간을 고려하지 않는다. 실제 사용에 있어서 응답시간은 매우 중요한 요소이지만, CAP 이론에서는 응답을 아무리 늦게 보내도 받기만 하면 된다.

네트워크 분할 허용 (Partition Tolerance)

네트워크의 어느 한 지점과 연결이 끊어져도 서비스가 중단되지 않음을 보장한다. 네트워크 장애로 메시지를 손실하더라도 시스템은 정상 동작해야 한다.

네트워크 노드간 통신이 어려워 네트워크가 사실상 분할되었을 때에도 최종 사용자 입장에서는 문제 없이 네트워크를 이용할 수 있어야 한다. 최종 사용자는 분산 네트워크가 여러 개의 노드로 나뉘었다는 사실을 인지하지 못하도록 해야 한다. 일부 노드간 연결이 끊어지더라도 우회하여 연결될 수 있다면 서비스는 중단되지 않는다.

모든 분산 네트워크는 네트워크 파티션 허용을 보유할 수 밖에 없다. 노드간 통신이 불안정하더라도 네트워크가 정상적으로 동작해야한다는 것이 분산 네트워크의 가장 중요한 특성이기 때문에, 분할 허용을 가정하지 않는다면 분산 네트워크라는 의미가 없어진다. CAP 이론에서 분할 허용은 기본으로 전제된다.

1-2. CAP의 상관관계

CAP 정리에 따르면 모든 분산 네트워크는 위의 3가지 특성 중 2가지만 달성 가능하다. 분산 네트워크에서는 네트워크 분할을 피할 수 없으므로 사실상 모든 분산 네트워크는 일관성과 가용성 둘 중 하나를 선택해야 함을 의미한다.

dApp 개발자는 finality 보장에 숨어 있는 트레이드 오프 관계를 이해하고 dApp의 성격에 맞는 적절한 체인을 선택하는 것이 좋다.

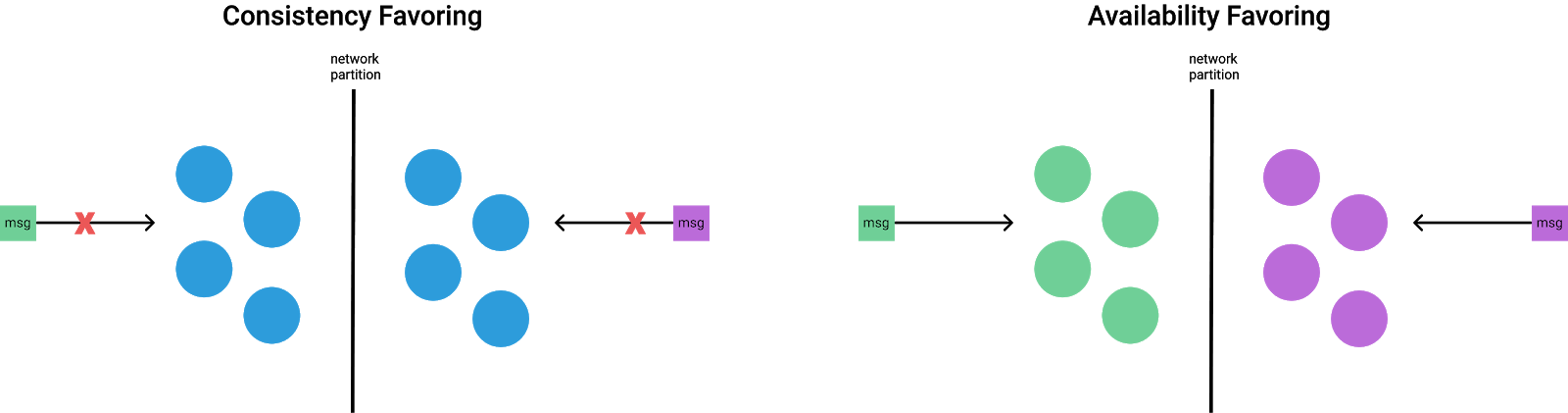
CP 시스템

절대적 finality를 선택한 체인은 네트워크 분할 상황에서 일관성(Consistency)를 보장한다.

완벽한 일관성을 갖는 분산 시스템에서의 데이터 변경은 모든 노드에 복제되어야 완료된다. 하나의 노드라도 문제가 있으면 트랜잭션은 실패한다. 노드가 늘어날수록 지연 시간은 길어진다.

AP 시스템

확률적 finality를 선택한 체인은 네트워크 분할 상황에서 가용성(Availabiltiy)를 보장한다.

완벽한 가용성을 갖는 분산 시스템에서는 모든 노드가 어떤 상황에서라도 응답할 수 있어야 한다. 네트워크에 문제가 발생하여 어떤 노드에 replication이 제대로 이루어지지 않아도 가용성을 위해 해당 노드에 접근한 사용자에게 데이터를 반환한다. 일관성이 깨지는 것은 당연하고 사용자는 문제 발생을 인지하지도 못할 것이다.

CA 시스템

일관성과 가용성을 동시에 만족하기 위해서는 네트워크 장애를 허용하지 않아야 한다. 하지만 이러한 네트워크는 구성이 불가능하다. P는 무조건 선택되어야 한다.

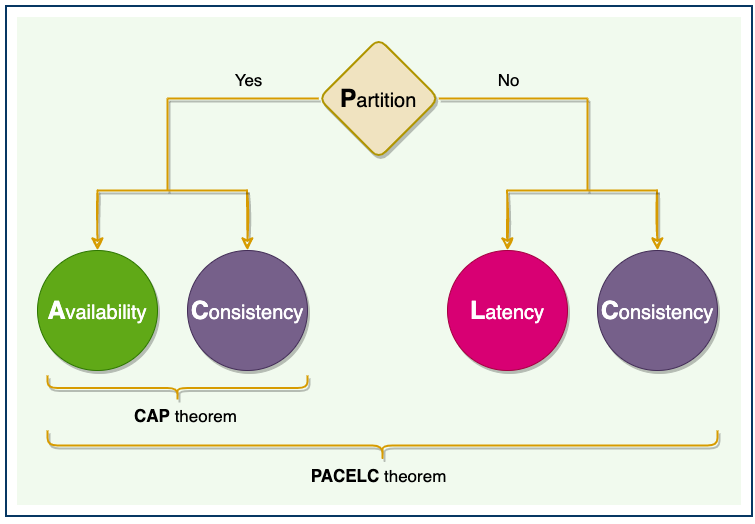
2. PACELC 이론

CAP 이론에 따르면 분산 시스템은 CP이거나 AP여야 한다.

완벽한 CP 시스템에서는 하나의 트랜잭션이 다른 모든 노드에 복제된 후에 트랜잭션이 완료된다. 이는 가용성 뿐만 아니라 성능의 희생을 필요로 한다. 단 하나의 노드라도 문제가 있다면 이 트랜잭션은 무조건 실패한다. 노드가 늘어날 수록 지연 시간은 길어진다. 완벽한 AP 시스템에서는 모든 노드가 어떤 상황에서라도 응답할 수 있어야 한다. 하나의 노드가 네트워크 분할로 고립되어 일관성이 깨졌다 하더라도 어쨌든 응답만 한다면 완벽한 가용성을 갖추게 된다.

따라서 완벽한 CP 시스템과 완벽한 AP 시스템은 쓸모가 없다. 이 상충관계에서는 둘 중 하나를 선택해야 하는 것이 아니라 일관성과 가용성의 허용 수준을 요구사항에 맞게 선택해야 한다. 하지만 CAP 이론은 네트워크이 분할되지 않은 정상 상황에 대해 설명하지 못한다.

PACELC 이론은 CAP 이론으로 부족한 부분을 보완하기 위해 네트워크 장애 상황과 정상 상황으로 나누어 설명하는 이론이다. 네트워크 분할이 발생했다면 CAP 이론에서 제시한 가용성과 일관성 사이의 trade-off가, 그렇지 않다면 지연시간과 일관성 사이의 trade-off가 있음을 의미한다.

• 네트워크 분할 상황 (CAP 이론)
  분할 상황은 물리적인 네트워크의 분할만을 의미하지 않고 노드끼리 데이터를 주고받을 때 타임아웃이 발생하는 모든 경우를 포함한다. 분할 상황에서는 단일 노드에 접근할 수 없기 때문에 일관성을 포기하고 가용성을 제공할지, 가용성을 포기하고 일관성을 유지할지의 정도를 결정해야 한다.

• 네트워크 정상 상황
  모든 노드에 업데이트를 반영해 일관성을 유지하기 위해 긴 대기/응답 시간을 가질지, 일관성을 포기하고 짧은 지연시간을 가질지의 정도를 결정해야 한다.

PACELC가 제시하는 분류 기준에 따라 비즈니스에 가장 적합한 방식을 선택해야 한다.

🖋 블록체인 시스템은?

CAP 이론의 관점에서 일반적으로 블록체인은 일관성보다는 가용성을 충족하는 AP 시스템이다. PACLEC 이론의 관점에서 블록체인은 일관성 보다 가용성과 지연시간을 중시한 분산 시스템이다. 하지만 충분한 완결성이 부여된 블록에 대해서는 높은 확률로 일관성을 보장하는 확률적 finality 분산 시스템이다. 현재 상태에 대해서는 가용성과 지연시간을, 과거 상태에 대해서는 일관성을 중시한다고 볼 수도 있다.

📌 Reference
https://kwangyulseo.com/2019/08/14/cap-%EC%A0%95%EB%A6%AC%EC%99%80-%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8-finality/
https://ohjongsung.io/2019/05/01/cap-%EC%9D%B4%EB%A1%A0%EA%B3%BC-pacelc-%EC%9D%B4%EB%A1%A0
https://luv-n-interest.tistory.com/854
https://medium.com/curg/%EB%8D%B0%EC%9D%B4%ED%84%B0%EB%B2%A0%EC%9D%B4%EC%8A%A4-%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8-%EA%B7%B8%EB%A6%AC%EA%B3%A0-%ED%8A%B8%EB%A6%B4%EB%A0%88%EB%A7%88-be05b0c7ddc1
http://happinessoncode.com/2017/07/29/cap-theorem-and-pacelc-theorem/