완전 검색(Exhaustive Search)
- 완전 검색 방법은 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법
- Brute-force 혹은 generate-and-test기법이라고도 불린다.
- 모든 경우의 수를 테스트 한 후 최종 해법을 도출
- 일반적으로 경우의 수가 상대적으로 적을 때 유용
- 상대적으로 빠른 시간에 알고리즘을 설계할 수 있다.
- 모든 경우의 수를 생성하고 테스트하기 때문에 수행 속도는 느리지만, 해답을 찾아내지 못할 확률이 적다.
- 검정 등에서 주어진 문제를 풀 때, 우선 완전 검색으로 접근하여 해답을 도출한 후, 성능 개선을 위해 다른 알고리즘을 사용하고 해답을 확인하는 것이 바람
직하다. - 전형적으로 순열(Permutation), 조합(Combination), 그리고 부분집합(subsets)과 같은 조합적 문제들(Combinational Problems)과 연관된다.
1. 순열(Permutation)
- 서로 다른 것들 중 몇 개를 뽑아서 한 줄로 나열하는 것
- 서로 다른 n개 중 r개를 택하는 순열 nPr로 나타낸다.
- 순열을 구성하는 방법으로는 아래 5가지가 존재한다.
- iterative한 방법
- swap을 통한 방법
- 방문처리를 통한 방법
- 비트마스킹을 통한 방법
- NextPermutation을 통한 방법(사전순)
- 아래 사진과 같이 nPn을 구한다고 했을 때, N이 10의 크기만 되어도 순열의 크기가 매우 커지기 때문에 N이 큰 경우에는 불가능한 경우도 있다.
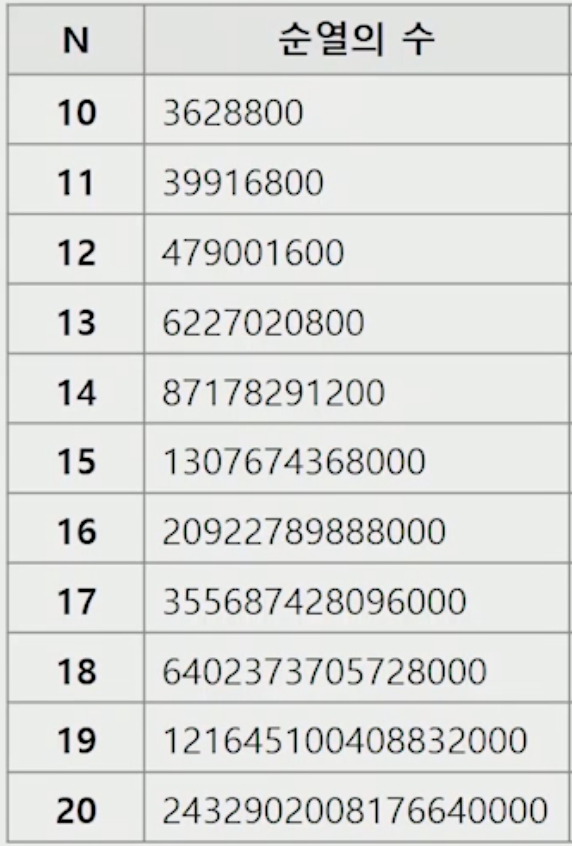
방법 1 - iterative
- 반복문을 통한 순열 생성
방법 2 - swap
- swap 함수를 만들어서 배열들의 값을 직접 바꾸는 방법
- 알고리즘
- 배열의 첫 값부터 순서대로 하나씩 바꾸며 모든 값을 한번씩 swap
- depth 를 기준 인덱스로 하여 depth 보다 인덱스가 작은 값들은 그대로 고정하고 depth 보다 인덱스가 큰 값들만 가지고 다시 swap 을 진행
- 간단하고 코드도 깔끔하게 나오지만 순열들의 순서가 보장되지 않음
// 사용 예시: permutation(arr, 0, n, 4);
static void permutation(int[] arr, int depth, int n, int r) {
if (depth == r) {
print(arr, r);
return;
}
for (int i = depth; i < n; i++) {
swap(arr, depth, i);
permutation(arr, depth + 1, n, r);
swap(arr, depth, i);
}
}
static void swap(int[] arr, int depth, int i) {
int temp = arr[depth];
arr[depth] = arr[i];
arr[i] = temp;
}
// 배열 출력
static void print(int[] arr, int r) {
for (int i = 0; i < r; i++)
System.out.print(arr[i] + " ");
System.out.println();
}방법 3 - 방문처리
- boolean[] 사용
- 재귀적으로!
| 코드
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int N;
static int[] input, numbers;
static boolean[] isSelected;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
input = new int[N];
numbers = new int[N];
isSelected = new boolean[N];
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
permutation(0);
}
public static void permutation(int cnt) {
if(cnt == N){
System.out.println(Arrays.toString(numbers));
return;
}
for (int i = 0; i < N; i++) {// 모든 수를 한 번씩 체크할 것이기 때문에!
if (isSelected[i])
continue;
numbers[cnt] = input[i];
isSelected[i] = true;
permutation(cnt + 1);
isSelected[i] = false;
}
}
}
방법 4 - 비트마스킹
- 비트연산자 사용
- 비트연산자
- &: 비트 단위로 AND 연산
- &연산에서 얻고자 하는 것은 내가 보는 위치의 비트가 1인지 여부를 확인하기 위함임
- |: 비트 단위로 OR 연산
- 상대비트랑 상관없이 내가 만들고 싶은 자리에 1로 마킹할 수 있음
- ^: 비트 단위로 XOR 연산(같으면 0, 다르면 1)
- ~: 단항 연산자로서 피연산자의 모든 비트를 반전시킴
- <<: 피연산자의 비트 열을 왼쪽으로 이동
- 비는 오른쪽 비트를 0으로 채움
- 2배씩 커짐
- >>: 피연산자의 비트 열을 오른쪽으로 이동
- 비는 왼쪽 비트를 부호비트로 채움
- >>>: 피연산자의 비트 열을 오른쪽으로 이동
- 비는 왼쪽 비트를 0으로 채움
- &: 비트 단위로 AND 연산
- flag: boolean[ ]을 대체
- if(flag & 1 << i): 조건판단(사용여부), &연산을 사용하여 i번째에 해당하는 수가 사용 중인지 아닌지 확인함.
- flag | 1 << i: 상태추가, i번째 값을 사용했다고 표시하기, 배열이 아니라 변수이기 때문에 flag값은 함수 내에서 변화 없음. 그렇기 때문에 매개변수 보낼 때만 변환된 값을 주면 됨.
코드
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int N;
static int[] input, numbers;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
input = new int[N];
numbers = new int[N];
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
permutation(0, 0);
}
public static void permutation(int cnt, int flag) {
if (cnt == N) {
System.out.println(Arrays.toString(numbers));
return;
}
for (int i = 0; i < N; i++) { // 모든 수를 한 번씩 체크할 것이기 때문에!
if ((flag & 1 << i) != 0)
continue;
numbers[cnt] = input[i];
permutation(cnt + 1, (flag | 1 << i));
}
}
}방법 5 - swap, NextPermutation
- nPn에서만 사용 가능
- 현 순열에서 사전 순으로 다음 순열 생성
- 알고리즘
- 아래 과정을 반복하여 사전식으로 다음으로 큰 순열 생성(가장 큰 내림차순 순열을 만들깨짜기 반복)
- 뒤쪽부터 탐색하며 교환위치(i-1) 찾기 (i: 꼭대기)
- 큰 수로 교환 해야하는 위치를 찾음
- 꼭대기가 없다는 말은 가장 큰 내림차순 순열을 의미하기 때문에 false return(종료!)
- 큰 수로 교환 해야하는 위치를 찾음
- 뒤쪽부터 탐색하며 교환위치(i-1)와 교환할 큰 값 위치(j)찾기
- 교환할 큰 값 위치: 자신보다 다음으로 큰 수(한 단계만 더 큰 수)
- i-1 교환위치값 보다 큰 값은 항상 존재
- 교환할 큰 값 위치: 자신보다 다음으로 큰 수(한 단계만 더 큰 수)
- 두 위치 값(i-1, j) 교환
- 꼭대기위치(i)부터 맨 뒤까지 오름차순 정렬
- 아래 사진처럼 swap
- 3번에서 값을 교환해도 i번째부터 맨 뒤까지는 내림차순을 유지하고 있다.
- 3번에서 값을 교환해도 i번째부터 맨 뒤까지는 내림차순을 유지하고 있다.
- 아래 사진처럼 swap
- 뒤쪽부터 탐색하며 교환위치(i-1) 찾기 (i: 꼭대기)
- 아래 과정을 반복하여 사전식으로 다음으로 큰 순열 생성(가장 큰 내림차순 순열을 만들깨짜기 반복)
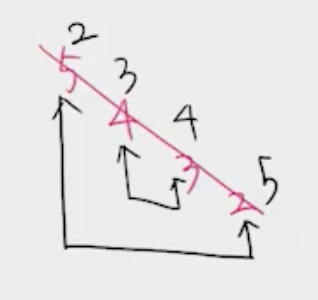
- NextPermutation 사용 전에 숫자 배열을 오름차순으로 정렬하여 가장 작은 순열 한 번 처리
코드
import java.util.Arrays;
import java.util.Scanner;
public class P4_PermutationNPTest {
static int N;
static int[] input;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
input = new int[N];
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
Arrays.sort(input); // 오름차순 정렬하여 가장 작은 순열의 상태로 만듦
do {
System.out.println(Arrays.toString(input));
} while (np());
}
public static boolean np() {
// 1. 꼭대기를 찾는 과정
int i = N - 1; // 뒤에서부터 search
while (i > 0 && input[i - 1] >= input[i]) --i;
// 더이상 앞자리가 없는 상황: 현 순열의 상태가 가장 큰순열(마지막 순열)
if (i == 0)
return false;
// 2. 꼭대기 앞자리(i-1)보다 한단계 큰 값을 찾는 과정
int j = N - 1;
while (input[i - 1] >= input[j]) --j;
// 3. 교환
swap(i - 1, j);
// 4. i부터 맨뒤까지 오름차순으로 정렬하는데 대칭구조로 정렬!
int k = N - 1;
while (i < k) {
swap(i++, k--); // 대칭으로 swap할 때, i는 뒤로가고, k는 앞으로 와야한다.
}
return true;
}
private static void swap(int i, int j) {
int temp = input[i];
input[i] = input[j];
input[j] = temp;
}
}
/*
3
2 4 5
혹은
4
1 2 3 4
*/
2. 조합(Combination)
- 조합이란 n 개의 숫자 중에서 r 개의 수를 순서 없이 뽑는 경우
- 예를 들어 [1, 2, 3] 이란 숫자 배열에서 2개의 수를 순서 없이 뽑으면
[1, 2]
[1, 3]
[2, 3]
이렇게 3 개가 나온다.
방법 1 - iterator
방법 2 - 재귀 recursion
코드
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int N, R;
static int[] input, numbers;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
R = sc.nextInt();
input = new int[N];
numbers = new int[R];
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
comb(0, 0);
}
public static void comb(int cnt, int start) {
if (cnt == R) {
System.out.println(Arrays.toString(numbers));
return;
}
for (int i = start; i < N; i++) {
numbers[cnt] = i;
comb(cnt + 1, i + 1);
}
}
}
/*
4 3
1 2 3 4
*/
방법 3 - NP
- Next Permutation으로 사전순 나열한 조합 생성
- 알고리즘
- 원소 크기와 같은 크기의 int 배열 P를 생성한다.
- 배열 Pdp r개 크기만큼 뒤에서 0이 아닌 값(ex. 1)으로 초기화
- nextPermutation 알고리즘 활용
- 이 알고리즘은 nextPermutation 알고리즘 한 번 수행할 때마다 조합이 만들어진다.
- P 배열에서 0이 아닌 값을 갖고 있는 위치에 해당하는 원소가 조합에 선택된 것을 의미한다.
- 원소를 직접적으로 다루지 않고 사용여부를 담은 배열 P를 사용하여 조작하는 것이다.
코드
import java.util.Scanner;
public class Main {
static int N, R;
static int[] input, P;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
R = sc.nextInt();
input = new int[N];
P = new int[N]; // N 크기의 flag 배열
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
int cnt = 0;
while (++cnt <= R)
P[N - cnt] = 1; // 전치연산을 했기 때문에 조건문에 등호를 포함함.
do {
for (int i = 0; i < N; i++)
if (P[i] == 1) System.out.print(input[i] + " ");
System.out.println();
} while (np());
}
public static boolean np() {
// 1. 꼭대기를 찾는 과정
int i = N - 1; // 뒤에서부터 search
while (i > 0 && P[i - 1] >= P[i])
--i;
// 더이상 앞자리가 없는 상황: 현 순열의 상태가 가장 큰순열(마지막 순열)
if (i == 0)
return false;
// 2. 꼭대기 앞자리(i-1)보다 한단계 큰 값을 찾는 과정
int j = N - 1;
while (P[i - 1] >= P[j])
--j;
// 3. 교환
swap(i - 1, j);
// 4. i부터 맨뒤까지 오름차순으로 정렬하는데 대칭구조로 정렬!
int k = N - 1;
while (i < k) {
swap(i++, k--); // 대칭으로 swap할 때, i는 뒤로가고, k는 앞으로 와야한다.
}
return true;
}
private static void swap(int i, int j) {
int temp = P[i];
P[i] = P[j];
P[j] = temp;
}
}
/*
* 4 3 1 2 3 4
*/
3. 부분집합(Subset)
방법 1 - iterative
- 반복문을 통해 부분집합 생성
- ex) {1,2,3} 집합의 모든 부분집합 (Power Set) 생성
방법 2 - 재귀 recursion
- 각 원소를 부분집합에 포함 여부의 형태로 재귀적으로 구현함
코드
import java.util.Scanner;
public class Main {
static int N, totalCnt;
static int[] input;
static boolean[] isSelected;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
input = new int[N];
isSelected = new boolean[N];
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
generateSubset(0);
}
private static void generateSubset(int cnt) {
if (cnt == N) {
++totalCnt;
for (int i = 0; i < N; i++) {
System.out.print((isSelected[i] ? input[i] : "X") + "\t");
}
System.out.println();
return;
}
// select
isSelected[cnt] = true;
generateSubset(cnt + 1);
// no select
isSelected[cnt] = false;
generateSubset(cnt + 1);
}
}
/*
3
1 2 3
*/
방법 3 - Binary Counting
- 원소 수에 해당하는 N개의 비트열 이용
- 비트값은 사용여부를 의미. 0이면 사용X, 1이면 사용O
코드
import java.util.Scanner;
public class Main {
static int N;
static int[] input;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
input = new int[N];
for (int i = 0; i < N; i++) {
input[i] = sc.nextInt();
}
generateSubset(1 << N);
}
// caseCount: 총 부분집합의 수
private static void generateSubset(int caseCount) {
for (int flag = 0; flag < caseCount; flag++) { // i: 비트마스크 되어 있는 수
for (int j = 0; j < N; j++) { // 맨뒤부터 N개의 비트열을 확인
if ((flag & 1 << j) != 0) {
System.out.print(input[j] + " ");
} else {
System.out.print("X ");
}
}
System.out.println();
}
}
}
/*
3
1 2 3
*/
나의 '개발'자국 🐾 | [이전 블로그] https://blog.naver.com/yoonjy1106