
시간복잡도란?
알고리즘이 문제를 해결하는 데 필요한 연산 횟수를 입력 크기의 함수로 표현한 것
계산하는 법
3x^2+5x+6 이면 최고차항 3x^2 만 생각하면 된다. 따라서 O(N^2)
x + logx 이면 로그함수는 증가폭이 훨씬 작으므로 O(N) 이다.
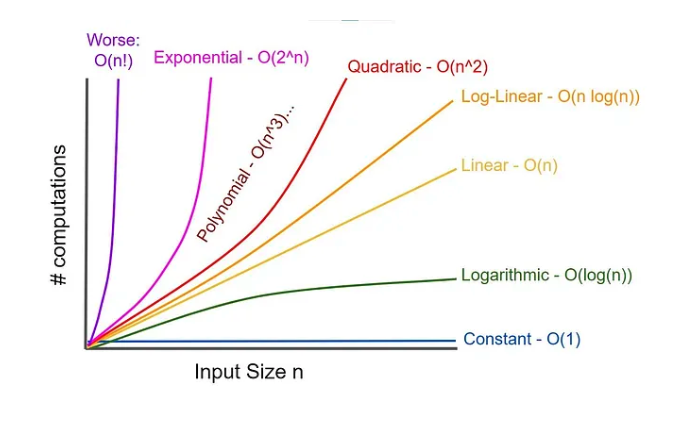
시간복잡도 그래프
함수마다 차이가 기하급수적으로 커지기 때문에 위에 계산식에서 최고차항이 아닌 나머지 함수들은 제거하는게 가능했던 것이다.
시간복잡도와 그에 따른 연산횟수 정리
| 시간 복잡도 | 최대 연산 횟수 |
|---|---|
| O(N!) | 10 |
| O(2^N) | 20~25 |
| O(N^3) | 200~300 |
| O(N^2) | 3,000~5,000 |
| O(NlogN) | 100만 |
| O(N) | 1,000~2,000만 |
| O(logN) | 10억 |
참고) 트리와 같이 탐색할 떄마다 탐색 대상이 반으로 줄어드는 경우는 시간복잡도가 O(logN) 이다.
실제 문제에서 적용하는법
코딩테스트 연습 - 짝지어 제거하기
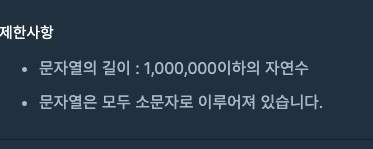
문자열의 길이가 백만 이하인데 이중 반복문인 n제곱 시간복잡도로 계산하면 무조건 시간초과가 난다.
따라서, 더 효율적인 스택과 같은 자료구조를 이용해야 한다.
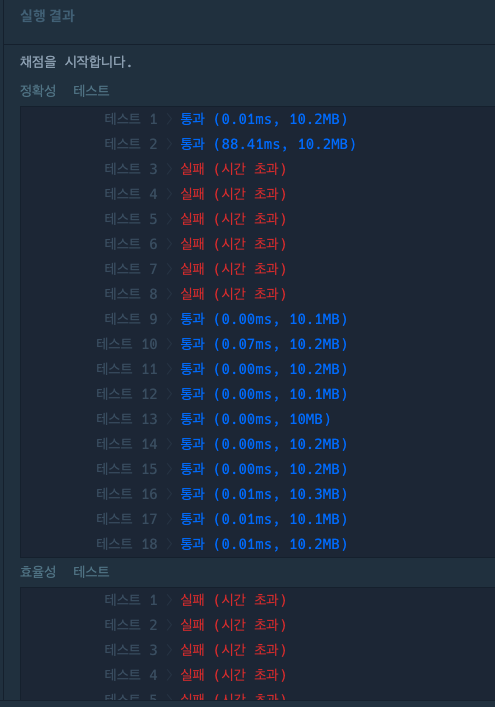
2중 반복문으로 짠 코드
def solution(s):
while len(s) > 0:
found_pair = False
for i in range(len(s) - 1):
if s[i] == s[i+1]:
s = s[:i] + s[i+2:]
found_pair = True
break
if not found_pair:
return 0
return 1논리구조는 맞지만 시간초과로 인한 오답이 된다.
스택구조 사용한 코드
def solution(s):
tmp = []
for a in s:
if not tmp: #예외처리
tmp.append(a)
else:
if tmp[-1] == a:
tmp.pop()
else:
tmp.append(a)
if not tmp:
return 1
return 0
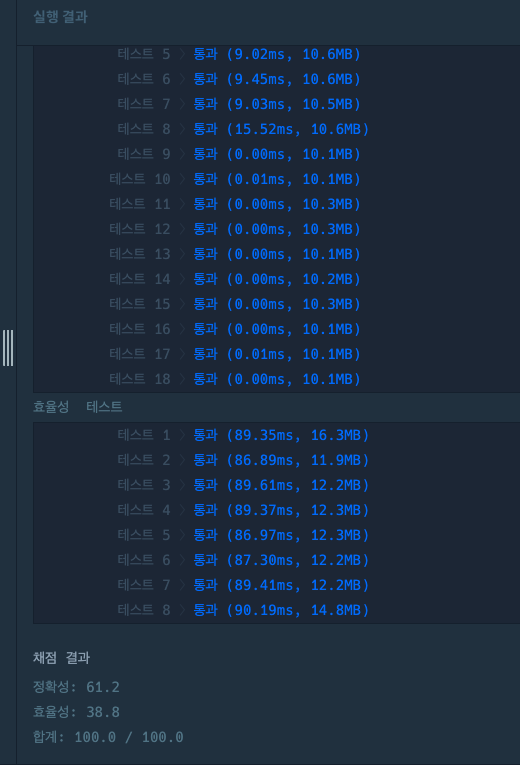
결론
코딩테스트 문제가 정답이 되려면 결국 정확성과 효율성 둘다를 만족시켜야 하는데, 논리적 구조뿐만이 아닌 적절한 자료구조와 알고리즘을 택해야 한다.
참고 자료
인프런 - 코딩 테스트 합격자 되기 - C++
코딩 테스트 합격자 되기 - 파이썬 편
https://medium.com/@buketsenturk/time-complexity-202eb4f1db40

