트리(Tree) 자료구조의 개념과 응용

1. 트리의 정의

트리는 계층적 관계를 나타내는 비선형 자료구조입니다. 노드(node)들과 이 노드들을 연결하는 간선(edge)들로 구성되어 있습니다. 트리는 다음과 같은 특징을 가집니다:

• 하나의 루트 노드를 가집니다.
• 각 노드는 0개 이상의 자식 노드를 가질 수 있습니다.
• 사이클(순환)이 존재하지 않습니다.

2. 트리의 주요 용어

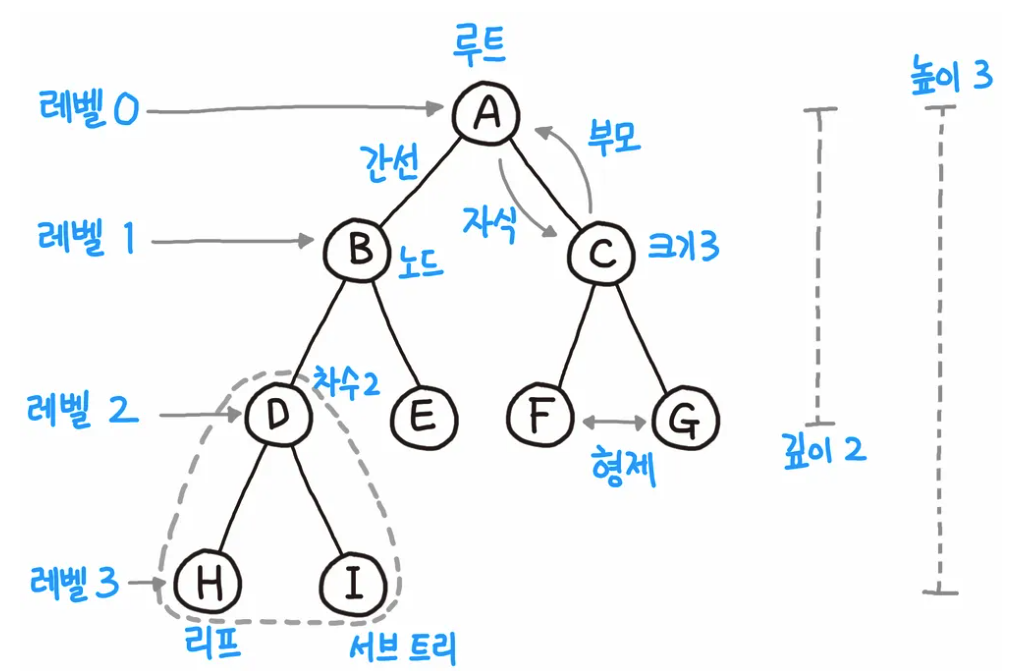
• 루트(Root): 트리의 최상위 노드
• 부모 노드(Parent Node): 직접 연결된 하위 노드를 가진 노드
• 자식 노드(Child Node): 부모 노드의 하위 노드
• 리프 노드(Leaf Node): 자식이 없는 노드
• 깊이(Depth): 루트에서 특정 노드까지의 경로 길이
• 높이(Height): 루트에서 가장 깊은 리프 노드까지의 경로 길이
• 레벨(Level): 같은 깊이를 가진 노드들의 집합

3. 트리의 종류

3.1 이진 트리(Binary Tree)

각 노드가 최대 두 개의 자식을 가질 수 있는 트리입니다.

3.1.1 완전 이진 트리(Complete Binary Tree)

마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있고, 마지막 레벨의 모든 노드는 가능한 한 왼쪽에 있는 이진 트리입니다.

3.1.2 포화 이진 트리(Full Binary Tree)

모든 내부 노드가 두 개의 자식을 가지고, 모든 리프 노드가 같은 레벨에 있는 이진 트리입니다.

3.1.3 균형 이진 트리(Balanced Binary Tree)

왼쪽과 오른쪽 서브트리의 높이 차이가 1 이하인 이진 트리입니다.

3.2 이진 탐색 트리(Binary Search Tree)

왼쪽 서브트리의 모든 노드 값이 현재 노드보다 작고, 오른쪽 서브트리의 모든 노드 값이 현재 노드보다 큰 이진 트리입니다.

3.3 AVL 트리

자가 균형 이진 탐색 트리로, 삽입과 삭제 후에 트리의 균형을 자동으로 맞춥니다.

3.4 레드-블랙 트리

자가 균형 이진 탐색 트리의 한 종류로, 각 노드에 색깔 속성을 추가하여 균형을 유지합니다.

3.5 B-트리

데이터베이스와 파일 시스템에서 널리 사용되는 자가 균형 트리입니다.

4. 트리의 구현

트리 기본구조

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.children = []

    def add_child(self, child_node):
        self.children.append(child_node)

이진 트리의 경우:

class BinaryTreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

5. 트리의 순회

트리 순회는 트리의 모든 노드를 체계적으로 방문하는 과정

1. 전위 순회(Preorder): 루트 -> 왼쪽 서브트리 -> 오른쪽 서브트리
2. 중위 순회(Inorder): 왼쪽 서브트리 -> 루트 -> 오른쪽 서브트리
3. 후위 순회(Postorder): 왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트

6. 트리의 응용

트리 구조는 다양한 분야에서 활용됩니다:

1. 파일 시스템 구조
2. 조직도
3. 계층적 데이터 표현 (XML, JSON)
4. 데이터베이스 인덱싱 (B-트리, B+트리)
5. 컴파일러에서의 구문 분석 트리
6. 결정 트리 알고리즘 (기계 학습)
7. 게임 AI의 의사결정 트리

7. 트리의 장단점

장점:

• 계층적 데이터를 효율적으로 저장하고 검색할 수 있습니다.
• 삽입과 삭제 연산이 비교적 빠릅니다.
• 일부 유형의 트리는 자동으로 정렬된 상태를 유지합니다.

단점:

• 일부 트리 유형은 구현과 유지가 복잡할 수 있습니다.
• 불균형한 트리는 성능이 저하될 수 있습니다.
• 순차적 접근에는 비효율적일 수 있습니다.

8. 결론

트리는 다양한 분야에서 널리 사용되는 중요한 자료구조입니다. 계층적 관계를 표현하는 데 탁월하며, 효율적인 검색과 정렬을 제공합니다. 다양한 변형과 응용이 존재하므로, 문제의 특성에 맞는 적절한 트리 구조를 선택하는 것이 중요합니다.

참고 자료
인프런 - 코딩 테스트 합격자 되기 - C++
코딩 테스트 합격자 되기 - 파이썬 편
트리(그래프)