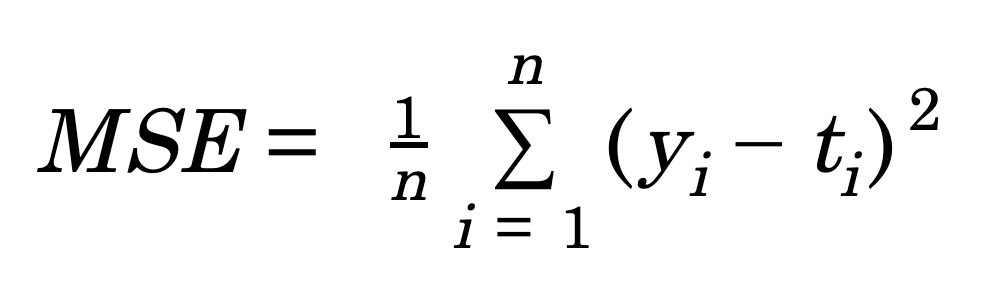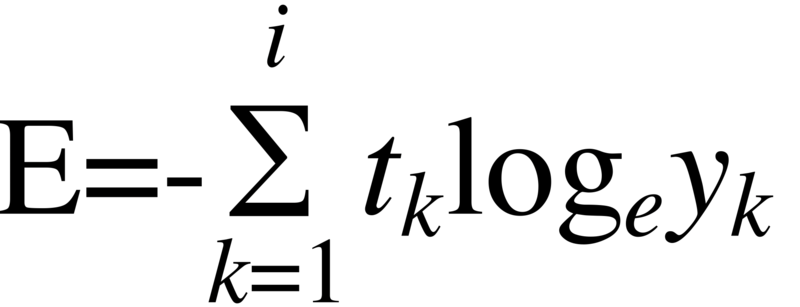손실, optimizer
손실함수 (Loss Function)
손실 함수는 실제값과 예측값의 차이(loss, cost)를 수치화해주는 함수
오차가 클수록 손실 함수의 값이 크고, 오차가 작을 수록 손실 함수의 값이 작아진다.
손실 함수의 값을 최소화 하는 W, b를 찾아가는 것이 학습 목표
회귀 : 평균제곱오차, 분류 : 크로스 엔트로피
평균제곱오차 (Mean Squared Error, MSE)
- 연속형 변수를 예측할 때 사용
def MSE(y, t): return (1/2) * np.sum((y-t)**2)
크로스 엔트로피(Cross- Entropy)
- 낮은 확률로 예측해서 맞추거나, 높은 확률로 예측해서 틀리는 경우 loss가 더 큼.
- 이진 분류 : binary_crossentropy
- 다중 분류: categorical_crossentropy
def cross_entrpy_error(y, t): delta = le - 7 return -np.sum(t * np.log(y + delta)) # y: 실제값(0혹은1), y^ : 예측값(확률)
최적화(Optimizer, 옵티마이저)
2-1: 경사하강법
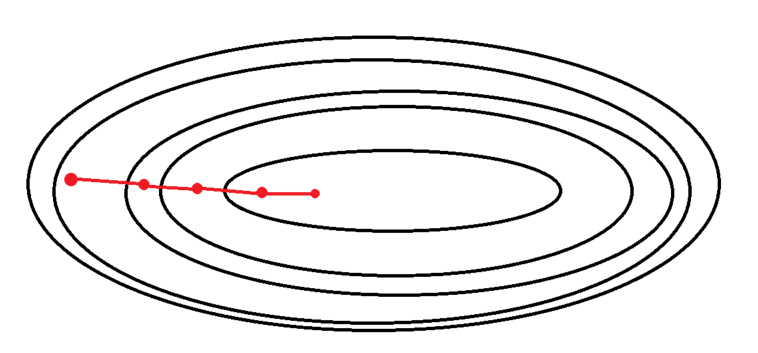
- 가장 기본적인 optimizer 알고리즘
- 경사를 따라 내려가면서 가중치를 업데이트
- 손실함수를 최소화하기 위하여 반복적으로 파라미터를 조정해나가는 방법
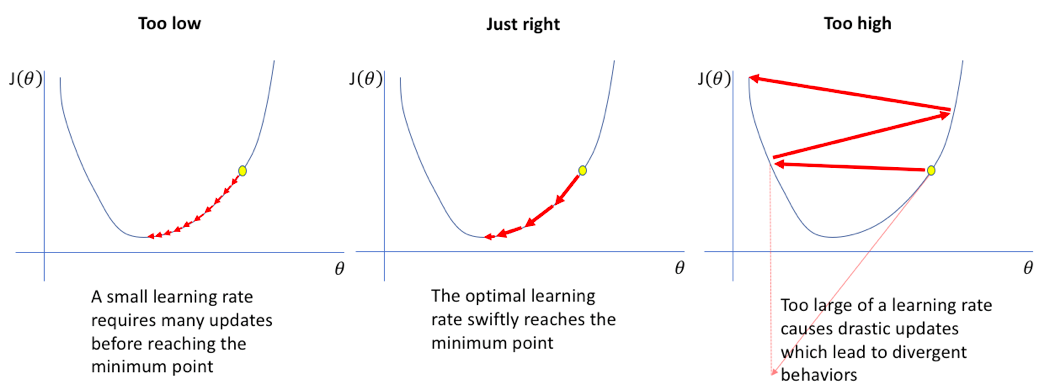
- 학습률이 너무크면 학습시간이 짧아지나 전역 최소값에서 멀어질 수 있음
- 학습률이 너무 작으면 학습 시간이 오래걸리고 지역 최솟값에 수렴할 수 있음
2-2: 배치 경사 하강법
- 전체 데이터를 통해 학습시키기 때문에, 가장 업데이트 횟수가 적다.
(1 Epoch 당 1회 업데이트)- 전체 데이터를 모두 한 번에 처리하기 때문에, 메모리가 가장 많이 필요하다.
- 항상 같은 데이터 (전체 데이터)에 대해 경사를 구하기 때문에, 수렴이 안정적이다.
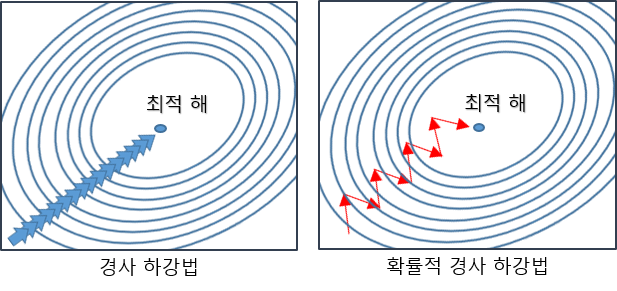
2-3: 확률적 경사 하강법(SGD)
- 매개변수 값을 조정 시 전체 데이터가 아니라 랜덤으로 선택한 하나의 데이터에 대해서만 계산하는 방법
- 더 적은 데이터를 사용하므로 더 빠르게 계산할 수 있다.
- 때로는 배치 경사 하강법 보다 정확도가 낮을 수 있다.
- 다른 기법들에 비해 비효율적
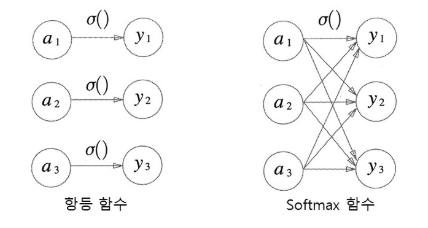
출력층의 활성화 함수
- 신경망은 분류와 회귀 모두에 이용할 수 있다.
- 일반적으로 회귀 문제에는 항등 함수를, 분류 문제에는 소프트 맥스 함수를 사용한다.
-
항등함수:
- 입력을 그대로 출력한다.
- 회귀 문제에 사용된다.
- 회귀 문제의 특성상 데이터 간의 연속적인 관계가 있어야하기 때문에 다른 활성화 함수가 필요 없다.
-
소프트 맥스 함수:
- 0과 1사이의 실수를 출력한다. 이때 출력값들의 합은 1이다.
- 분류 문제에서 사용된다.(두 종류로 분류하는 문제는 시그모이드 함수가 사용된다.)
- 활성화되기 전의 출력값들을 전체와의 비율(확률)로 나타내주는 활성화 함수
- 지수함수 때문에 오버플로우가 생길 수 있음.
-
tanh 함수:
- tanh 함수는 함수의 중심점을 0으로 옮겨 sigmoid가 갖고 있던 최적화 과정에서 느려지는 문제를 해결했다.
하지만 여전히 미분함수에 대해서 일정한 값이 지나면 vanishing gradient가 소실되는 단점을 지니고 있다.
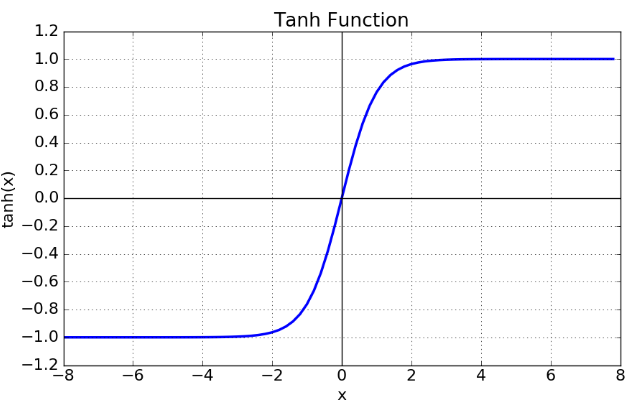
- tanh 함수는 함수의 중심점을 0으로 옮겨 sigmoid가 갖고 있던 최적화 과정에서 느려지는 문제를 해결했다.
-
Relu 함수:
- sigmoid, tanh함수보다 연산속도가 빠름.
- 0보다 작은 음수에 대해서는 함수 값이 0으로 나오므로 뉴런이 죽을 수도 있다는 단점이 있음.
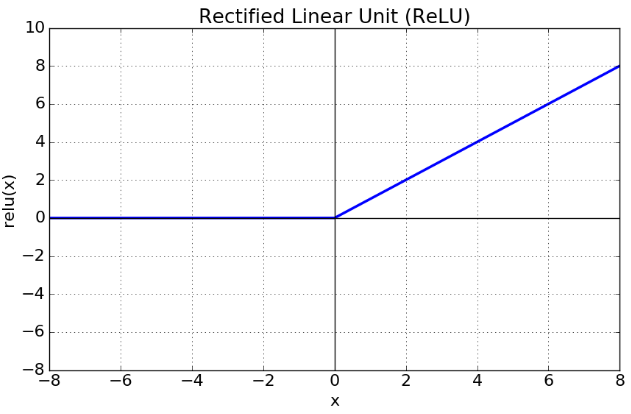
-
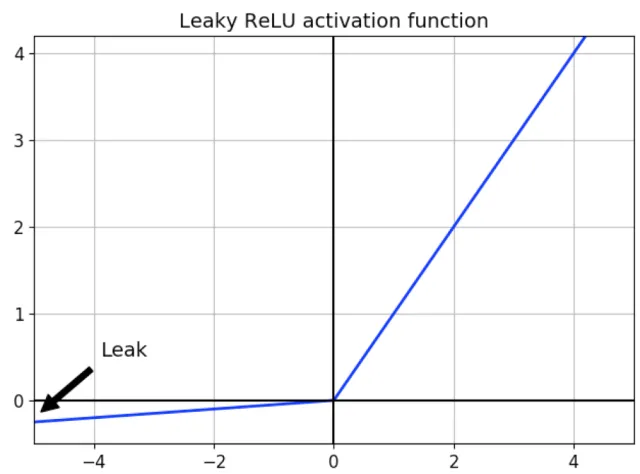
Leaky Relu 함수:
- Relu 함수에서 뉴런이 죽을수도 있다는 단점을 보완하기 위해 만듦.
- 리키렐루는 음수값을 0.01배를 하여 Dying relu를 방지함