Queue

1. First-In-First-Out

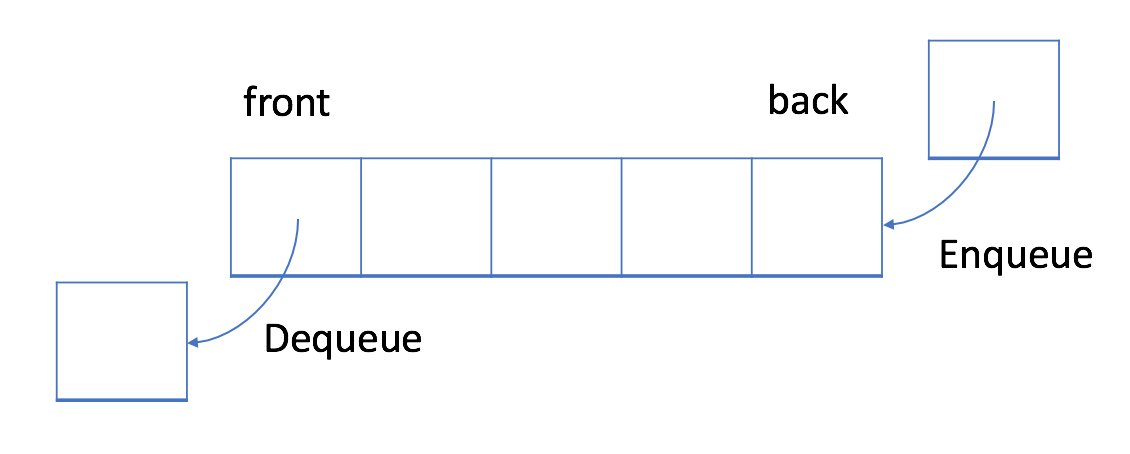
Queue is a linear structure with a FIFO characteristic
In FIFO structure - First element added to the queue will be processed first

Operations on queue

• Enqueue : Add items into end of queue
• Dequeue : Remove the first element of queue
• isEmpty : Check if queue is empty
• isFull : Check if queue is full
• Peek : Get front value of queue without removing it

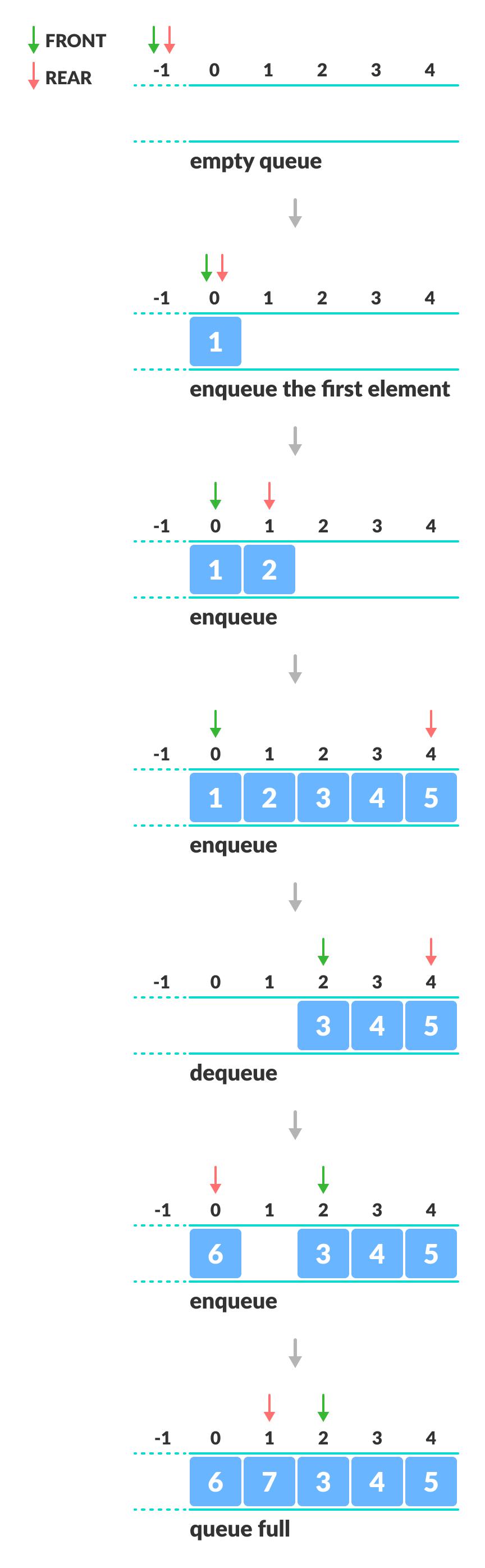
Linear Queue

For the linear queue, array was used and 2 pointers to track the start and end of queue

Working of queue

• Two pointers : front and rear
• front : track the first element of queue
• rear : track the last element of queue
• Initially set front and rear value to -1

Enqueue operation

• Check if queue is full
• For first element (if front==-1), set front to 0
• increase rear by 1
• Add new element to position pointed by rear

Dequeue operation

• Check if queue is empty
• Return value pointed by front
• Increase front index by 1
• For last element, set front and rear to -1

class Queue {
   private:
  int items[SIZE], front, rear;

   public:
  Queue() {
    front = -1;
    rear = -1;
  }

  bool isFull() {
    if (front == 0 && rear == SIZE - 1) {
      return true;
    }
    return false;
  }

  bool isEmpty() {
    if (front == -1)
      return true;
    else
      return false;
  }

  void enQueue(int element) {
    if (isFull()) {
      cout << "Queue is full";
    } else {
      if (front == -1) front = 0;
      rear++;
      items[rear] = element;
      cout << endl
         << "Inserted " << element << endl;
    }
  }

  int deQueue() {
    int element;
    if (isEmpty()) {
      cout << "Queue is empty" << endl;
      return (-1);
    } else {
      element = items[front];
      if (front >= rear) {
        front = -1;
        rear = -1;
      } /* Q has only one element, so we reset the queue after deleting it. */
      else {
        front++;
      }
      cout << endl
         << "Deleted -> " << element << endl;
      return (element);
    }
  }

The implementation is easy to understand however is highly inefficient. With the movement of the front pointer, there will be more and more wasted space as front pointer moves to next array.

Therefore to solve problem, circular queue is introduced

Circular Queue

Circular Queue is a linear data structure in which we use a fixed-size array and two pointers to indicate the starting position and the ending position. And the goal is to reuse the wasted storage we mentioned previously.

Circular Queue works by the process of circular increment

When we try to increment the pointer and we reach the end of the queue, we start from the beginning of the queue.

Circular queue operations

• Two pointers : front and rear
• front : track the first element of queue
• rear : track the last element of queue
• Initially set front and rear value to -1

Enqueue operation

• Check if queue is full
• For first element (if front==-1), set front to 0
• increase rear by 1 (i.e. if the rear reaches the end, next it would be at the start of the queue)
• Add new element to position pointed by rear

Dequeue operation

• Check if queue is empty
• Return value pointed by front
• Increase front index by 1
• For last element, set front and rear to -1

Difference of linear queue : Check whether queue is full

• Case 1 : front==0 && rear==size-1
• Case 2 : front == rear+1 -> When rear starts from 0 due to circular increment and when its value is just 1 less thatn front

// Check if the queue is full
  bool isFull() {
    if (front == 0 && rear == SIZE - 1) {
      return true;
    }
    if (front == rear + 1) {
      return true;
    }
    return false;
  }
  // Check if the queue is empty
  bool isEmpty() {
    if (front == -1)
      return true;
    else
      return false;
  }
  // Adding an element
  void enQueue(int element) {
    if (isFull()) {
      cout << "Queue is full";
    } else {
      if (front == -1) front = 0;
      rear = (rear + 1) % SIZE;
      items[rear] = element;
      cout << endl
         << "Inserted " << element << endl;
    }
  }
  // Removing an element
  int deQueue() {
    int element;
    if (isEmpty()) {
      cout << "Queue is empty" << endl;
      return (-1);
    } else {
      element = items[front];
      if (front == rear) {
        front = -1;
        rear = -1;
      }
      // Q has only one element,
      // so we reset the queue after deleting it.
      else {
        front = (front + 1) % SIZE;
      }
      return (element);
    }
  }