오늘의 한 마디
원형 dp 문제는, 케이스를 나누어서 INF로 고정해야 한다.
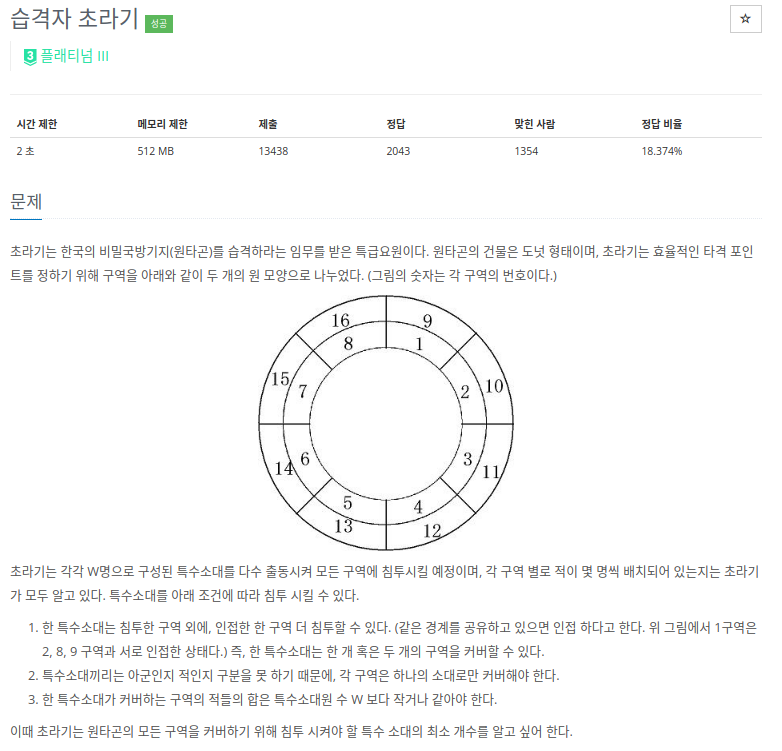
문제
1000번부터 깨던 유저들을 좌절하게 만든 그 문제다.
사실 플래티넘 3이었다는거...

발상
Try #1: dp로 푼줄 알았는데, 사실 그리디. 틀렸습니다
import sys
input = lambda: sys.stdin.readline().rstrip()
miis = lambda: map(int, input().split())
OUTER, INNER = 0, 1
NONE, HORIZONTAL, VERTICAL = 0, 1, 2
T = int(input())
for _ in range(T):
N, W = miis()
enemies = []
for _ in range(2):
enemies.append(list(miis()))
ans = 2*N
connected = [[NONE]*N for _ in range(2)]
# Step 1: 바깥 가로, 안쪽 가로 검사하기
for i in range(1, N):
if not connected[OUTER][i-1] and enemies[OUTER][i-1] + enemies[OUTER][i] <= W:
connected[OUTER][i-1], connected[OUTER][i] = HORIZONTAL, HORIZONTAL
ans -= 1
if not connected[INNER][i-1] and enemies[INNER][i-1] + enemies[INNER][i] <= W:
connected[INNER][i-1], connected[INNER][i] = HORIZONTAL, HORIZONTAL
ans -= 1
# Step 2: 세로 검사하기
# 가로들을 최대한 많이 만드는게 중요
for i in range(N):
if not connected[OUTER][i] and not connected[INNER][i] and \
enemies[OUTER][i] + enemies[INNER][i] <= W:
connected[OUTER][i], connected[INNER][i] = VERTICAL, VERTICAL
ans -= 1
# Step 3: 원형으로 만들기
if N == 1:
print(ans)
continue
if not connected[OUTER][N-1] and not connected[OUTER][0] and \
enemies[OUTER][N-1] + enemies[OUTER][0] <= W:
connected[OUTER][N-1], connected[OUTER][0] = HORIZONTAL, HORIZONTAL
ans -= 1
if not connected[INNER][N-1] and not connected[INNER][0] and \
enemies[INNER][N-1] + enemies[INNER][0] <= W:
connected[INNER][N-1], connected[INNER][0] = HORIZONTAL, HORIZONTAL
ans -= 1
if connected[OUTER][N-1] == VERTICAL and not connected[OUTER][0] and \
enemies[OUTER][N-1] + enemies[OUTER][0] <= W and \
enemies[INNER][N-1] + enemies[INNER][0] <= W:
enemies[OUTER][N-1], enemies[OUTER][0] = HORIZONTAL, HORIZONTAL
enemies[INNER][N-1], enemies[INNER][0] = HORIZONTAL, HORIZONTAL
ans += 1 # verti임에도 불구하고 깨고 두개를 이어주는게 낫다.
ans -= 2
print(ans)틀린 코드를 장황하게 써놓은 것 같다...
Try #1의 발상은,
세로로 연결하면, 가로 두쌍을 연결할 수 있는 걸 막기 때문에 최대한 가로를 만드는게 좋겠다는 생각에서 비롯된 것이었다.
그래서 앞에서부터 최대한 되는대로 가로 페어를 만들고, 그 남은 공간 중에 세로 페어가 되는 곳에 끼워넣는 방식으로 코딩했다.
그런데 이 풀이는 dp가 아니라 그리디다. 단단히 착각했다.
대표적인 반례를 하나 들자면,
3 3
1 2 1
3 1 3이 있겠다.
가로를 앞에서부터 만들려면, 왼쪽 위의 1 2를 페어로 만들어야겠지만,
사실 왼쪽 위의 1은 오른쪽 위의 1과 페어를 만들고 가운데 세로 2 1을 페어로 또 만드는게 최솟값이다.
해설을 보기 전에...
사실 문제를 읽고 나면, 정해를 생각해내긴 어려워도 다음과 같은 생각은 떠올릴 수 있다.
2xn 타일링에 원형 dp 문제를 합쳐놓은 것 같은데?
위 문제들과 차이점을 비교해보면,
이 문제는 원형 2xn 타일링(하지만 1x1 블럭도 쓸 수 있는...) 이라고 할 수 있겠다.
2xn 타일링의 풀이법
- dp 정의 :
dp[i]는, 2xi에서 채울 수 있는 직사각형의 경우의 수 - 초기값 설정 : dp[1] = 1, dp[2] = 2
- 점화식 생각해내기 = dp[N-1], dp[N-2]를 이용해서 어떻게 해서든 dp[N]을 구해봐야지.
- dp[N-1]에서 dp[N]으로 가는 경우는, 세로 직사각형을 넣는 경우의 수 하나밖에 없다.
- dp[N-2]에서 dp[N]으로 바로 가는 경우는, 가로 직사각형을 두개 넣는 경우의 수 하나밖에 없다. (세로 직사각형 두개는, dp[N-1]에서 이미 셈.)
- 그러니, dp[N] = dp[N-1] + dp[N-2] 이겠네.
RGB거리 2의 풀이법
RGB거리 1의 내용 : 각 집을 R,G,B로 칠하는 비용이 각각 주어졌을 때, 옆집과 다른 색으로 칠하는 방법 중 가장 싼 방법 구하기
for i in range(2, N+1): dp[i][R] = min(dp[i-1][G], dp[i-1][B]) + houses[i][R] dp[i][G] = min(dp[i-1][R], dp[i-1][B]) + houses[i][G] dp[i][B] = min(dp[i-1][R], dp[i-1][G]) + houses[i][B]
RGB거리 2는, 마지막 집과 첫 집이 연결되어있다는 점만 다르다.
소위 원형 dp 문제를 어떻게 풀어냈을까?
for color in [R,G,B]:
dp[1] = [INF, INF, INF]
dp[1][color] = cost[1][color]
# RGB거리 1의 코드
# for i in range(2, N+1):
# dp[i][R] = min(dp[i-1][G], dp[i-1][B]) + cost[i][R]
# dp[i][G] = min(dp[i-1][R], dp[i-1][B]) + cost[i][G]
# dp[i][B] = min(dp[i-1][R], dp[i-1][G]) + cost[i][B]
dp[N][color] = INF
answer = min(answer, min(dp[N]))-
case를 세개로 나눈다. (첫 집이 이미 R/G/B인 경우)
-
첫 집에 반드시 R/G/B를 택하도록 하기 위해서,
그것을 제외한 색깔에는 비용을 INF로 둔다. -
마지막 집이 R/G/B를 택한 비용은 제외하여,
반드시 마지막 집이 R/G/B가 아닐 경우만 센다.
해설
https://kibbomi.tistory.com/128
위 링크의 해설에서는,
2xn 타일링의 풀이법과 RGB거리 2의 풀이법이 모두, 그리고 훨씬 응용되어 들어가 있다.
풀이
해설 링크의 풀이를 Pythonic하게 다시 짜보았다.
import sys
input = lambda: sys.stdin.readline().rstrip()
miis = lambda: map(int, input().split())
INF = int(1e9)
OUT, IN, BOTH = 0, 1, 2
def f(dp, outer, inner):
for i in range(1, N):
outer_squad = 1 if outer[i-1] + outer[i] <= W else 2
inner_squad = 1 if inner[i-1] + inner[i] <= W else 2
verti_squad = 1 if outer[i] + inner[i] <= W else 2
dp[i][OUT] = min(dp[i-1][IN] + outer_squad, dp[i-1][BOTH] + 1)
dp[i][IN] = min(dp[i-1][OUT] + inner_squad, dp[i-1][BOTH] + 1)
dp[i][BOTH] = min(dp[i-1][BOTH] + verti_squad, \
dp[i-2][BOTH] + outer_squad + inner_squad, \
dp[i-1][IN] + outer_squad + 1, \
dp[i-1][OUT] + inner_squad + 1)
def case1(): # outer, inner 둘다 연결 안됨(default)
dp = [[0]*3 for _ in range(N)]
dp[0][OUT] = dp[0][IN] = 1
dp[0][BOTH] = 1 if outer[0] + inner[0] <= W else 2
outer_cpy, inner_cpy = outer[:], inner[:]
f(dp, outer_cpy, inner_cpy)
return dp[N-1][BOTH]
def case2(): # outer만 연결된다면?
if outer[0] + outer[N-1] > W:
return INF
dp = [[0]*3 for _ in range(N)]
dp[0][OUT] = dp[0][IN] = 1
dp[0][BOTH] = 2
outer_cpy, inner_cpy = outer[:], inner[:]
outer_cpy[0] = outer_cpy[N-1] = INF
f(dp, outer_cpy, inner_cpy)
return dp[N-1][IN]
def case3(): # inner만 연결된다면?
if inner[0] + inner[N-1] > W:
return INF
dp = [[0]*3 for _ in range(N)]
dp[0][OUT] = dp[0][IN] = 1
dp[0][BOTH] = 2
outer_cpy, inner_cpy = outer[:], inner[:]
inner_cpy[0] = inner_cpy[N-1] = INF
f(dp, outer_cpy, inner_cpy)
return dp[N-1][OUT]
def case4(): # outer, inner 둘다 연결된다면?
if outer[0] + outer[N-1] > W:
return INF
if inner[0] + inner[N-1] > W:
return INF
dp = [[0]*3 for _ in range(N)]
dp[0][OUT] = dp[0][IN] = 1
dp[0][BOTH] = 2
outer_cpy, inner_cpy = outer[:], inner[:]
outer_cpy[0] = outer_cpy[N-1] = INF
inner_cpy[0] = inner_cpy[N-1] = INF
f(dp, outer_cpy, inner_cpy)
return dp[N-2][BOTH]
T = int(input())
for _ in range(T):
N, W = miis()
outer = list(miis())
inner = list(miis())
if N == 1:
print(1 if outer[0] + inner[0] <= W else 2)
continue
ans1 = case1()
ans2 = case2()
ans3 = case3()
ans4 = case4()
print(min(ans1, ans2, ans3, ans4))