오늘의 한 마디
이걸 어떻게 알아?

• Baekjoon 문제 링크
• 현재 백준 문제집: 단기간 성장을 풀고 있습니다.

문제

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

입력

트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.

먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

예제 입력 1

5
1 3 2 -1
2 4 4 -1
3 1 2 4 3 -1
4 2 4 3 3 5 6 -1
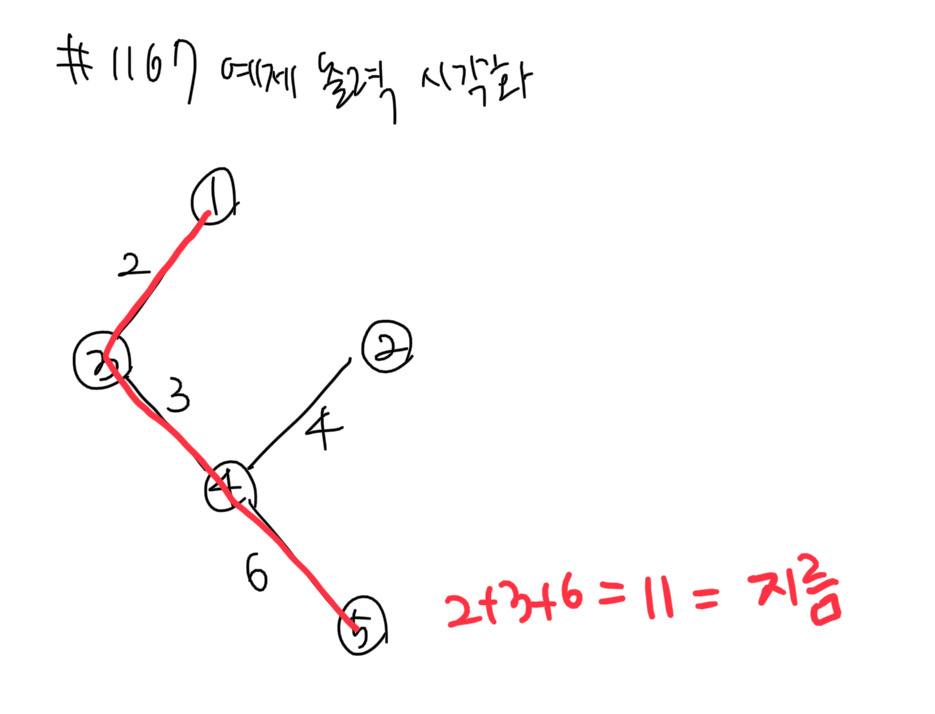
5 4 6 -1

예제 출력 1

11

발상

어디가 부모이고, 어디가 왼쪽 자식, 오른쪽 자식인지 궁금한가?

트리의 정의(조건)

잠시 트리의 정의 글의 내용을 빌려오자면,

트리의 정의는 다음과 같다.

트리란 사이클이 없이 모든 정점이 연결되어있는 그래프다. 사이클이 없는 그래프이므로 정점의 개수가 V개이면 간선의 개수는 V-1개이다.

여기서 한 가지 주목해야 할 점은, 왼쪽 자식이 어쩌구, 오른쪽 자식이 어쩌구 이딴 얘기는 트리의 정의에 포함되지 않는다는 점이다.

또한, 루트가 있어야 한다는 조건 이런것도 없다. 보통 트리에서 하도 루트를 언급하다 보니 루트가 당연히 있어야 한다고 생각할 수 있는데, 루트가 없는 트리도 존재한다.

트리는 그저 사이클이 없이 모든 정점이 연결되어있는 그래프이므로, 하나의 노드에 자식 노드가 여러개일 수 있다.

트리의 정의에는 왼쪽 자식, 오른쪽 자식은 커녕 자식이라는 용어 자체가 없다.
왼쪽 자식, 오른쪽 자식이라는 말은 트리 중에서도 이진 트리(Binary Tree)에만 적용되는 용어다.

이진 트리는, 루트 있는 트리 중에서도 자식을 최대 2개만 가지고 있는 트리이다.

항상 2개가 아니라는 점을 명심할 것!

자식을 항상 2개 가지고 있는 트리는 완전 이진 트리(Complete Binary Tree)이다.

트리의 지름 찾는 법

솔직히 구글링 없이 스스로 알아냈다면 천재다.

이 링크에 트리의 지름 찾는 법이 나와있다.

선형 시간안에 트리에서 지름을 구하는 방법은 다음과 같다:

1. 트리에서 임의의 정점 x를 잡는다.
2. 정점 x에서 가장 먼 정점 y를 찾는다.
3. 정점 y에서 가장 먼 정점 z를 찾는다.

이때, 트리의 지름은 정점 y와 정점 z를 연결하는 경로다.

여기서 핵심은,
1. 트리에서 아무 정점이나 잡고
2. dfs/bfs를 통해 가장 먼 비용을 갖는 정점을 찾아낸다면,
3. 그 정점은 반드시 트리의 지름을 이루는 정점 중 하나가 된다는 사실이다!

풀이

import sys
from collections import defaultdict

V = int(sys.stdin.readline().rstrip())
tree = defaultdict(list)

for _ in range(V):
    raw_str = list(map(int, sys.stdin.readline().rstrip().split()))
    num_from = raw_str[0]
    for i in range(1, len(raw_str)-1, 2):
        num_to = raw_str[i]
        cost_to = raw_str[i+1]
        tree[num_from].append((num_to, cost_to))

costs = [-1] * (V+1)

def dfs(num_from): # 사이클이 없는 그래프이므로 다시 돌아오지 않아, visited가 필요 없다. 
    for num_to, cost_to in tree[num_from]:
        if costs[num_to] == -1:
            costs[num_to] = costs[num_from] + cost_to
            dfs(num_to)

costs[1] = 0
dfs(1)
idx = costs.index(max(costs))

costs = [-1] * (V+1)
costs[idx] = 0
dfs(idx)
print(max(costs))

dfs(1)을 통해 트리의 지름을 이루는 정점 중 하나를 찾아내고,
(dfs(idx))를 통해 다른 하나의 정점까지 찾아낸다.