백준 #2042 구간 합 구하기 (파이썬) : 세그먼트 트리, 펜윅 트리 두가지 풀이

Yongjun Park·2022년 7월 11일

PS(Problem Solving)

목록 보기

28/31

오늘의 한 마디
드디어 세그먼트 트리를 알게 되었다.

Baekjoon 문제 링크

문제

어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 만약에 1,2,3,4,5 라는 수가 있고, 3번째 수를 6으로 바꾸고 2번째부터 5번째까지 합을 구하라고 한다면 17을 출력하면 되는 것이다. 그리고 그 상태에서 다섯 번째 수를 2로 바꾸고 3번째부터 5번째까지 합을 구하라고 한다면 12가 될 것이다.

입력

첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄까지 N개의 수가 주어진다. 그리고 N+2번째 줄부터 N+M+K+1번째 줄까지 세 개의 정수 a, b, c가 주어지는데, a가 1인 경우 b(1 ≤ b ≤ N)번째 수를 c로 바꾸고 a가 2인 경우에는 b(1 ≤ b ≤ N)번째 수부터 c(b ≤ c ≤ N)번째 수까지의 합을 구하여 출력하면 된다.

입력으로 주어지는 모든 수는 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.

출력

첫째 줄부터 K줄에 걸쳐 구한 구간의 합을 출력한다. 단, 정답은 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.

예제 입력 1

예제 출력 1

17
12

세그먼트 트리로 풀어보기

자주 바뀌는 누적 합 = 세그먼트 트리

중간에 수의 변경이 빈번히 일어나는 누적 합을 구하려고 고안된 것이 바로 세그먼트 트리다.

기존에는 누적 합 문제를 위 그림의 방식대로 풀었다.

하지만 이번 문제의 경우에는 중간에 수의 변경이 빈번하다는 점이 큰 걸림돌이다.
매번 그 인덱스 뒤에 있는 누적 합 배열을 모두 갱신해야 하므로, O(N)의 연산을 수행해야 한다.
(물론 찾을 때는 O(1)이지만)

하지만 오늘 소개할 세그먼트 트리나 펜윅 트리 풀이법을 이용하면,
변경할 때 O(logN), 찾을 때 O(logN)만에 찾을 수 있기 때문에 수행 시간을 줄일 수 있다!

세그먼트 트리의 기본 발상

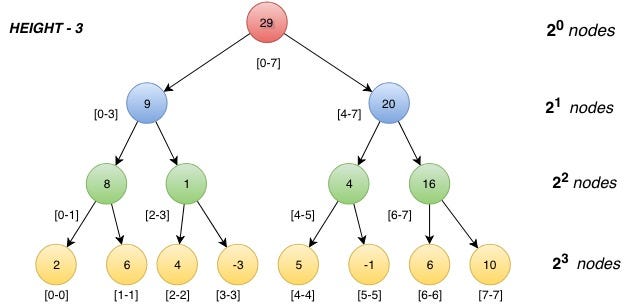
어떻게 변경할 때 O(logN), 찾을 때 O(logN)밖에 안 걸리는가?

변경할 때

위 그림을 보면 아주 쉽게 이해할 수 있다.
예를 들어, 2번 값을 4에서 10으로 변경한다고 하자.

그렇다면, [2-2] 정보를 저장하는 노드에 +6을 해서 10으로 만든다.
그 다음에는 거슬러 올라가면서 자신의 부모 노드만 갱신해주면 된다.
(트리를 어떻게 거슬러 올라가는지는 추후 설명하도록 하겠다.)

[2-3]에 +6을 해서 7로 만든다.
[0-3]에 +6을 해서 16으로 만든다.
[0-7]에 +6을 해서 35로 만든다.

# arr[IDX]를 DIFF만큼 변경했을 때의 tree 변경
def update(l, r, node, IDX, DIFF):
    if not (l <= IDX <= r):
        return
    tree[node] += DIFF
    if l == r:
        return
    mid = (l+r) // 2
    update(l, mid, node*2, IDX, DIFF)
    update(mid+1, r, node*2+1, IDX, DIFF)

tree[node]에 들어있는 값이 구간 [l, r]의 합이 될 것이다.

찾을 때

예를 들어, [1-5]의 구간 합을 구하고 싶다고 가정하자.
([2]를 +6 했던 예시는 잊어버리도록 하자.)

이때는 거꾸로 위에서부터 아래로 내려온다.
재귀적으로 내려가면서, [1-5]에 완전히 포함되는 노드가 있다면 sum에 추가하는 것이다!

[0-7]은 [1-5]에 포함되지 않는다. 그러니 sum에 29를 더하지 않고 계속 탐색한다.
[0-3]은 [1-5]에 포함되지 않는다. 그러니 sum에 9를 더하지 않고 계속 탐색한다.
[2-3]은 [1-5]에 완전히 포함된다. sum에 1을 더한다. 더 깊이 들어가지 않는다.

뭐.. 이런 식으로 진행하다보면
[0-0] [1-1] [2-2] [3-3] [4-4] [5-5]가 선택되는 게 아니라,
[1-1] [2-3] [4-5] 세 노드 값의 합으로 구간 합이 계산된다!

# [LEFT, RIGHT]의 구간 합을 구함.
def interval_sum(l, r, node, LEFT, RIGHT):
    if r < LEFT or RIGHT < l: # [l, r]이 [LEFT, RIGHT]를 완전히 벗어남. 
        return 0
    if LEFT <= l and r <= RIGHT: # [l, r]이 [LEFT, RIGHT] 안에 완전히 포함됨. 
        return tree[node]
    mid = (l+r) // 2
    return interval_sum(l, mid, node*2, LEFT, RIGHT) + interval_sum(mid+1, r, node*2+1, LEFT, RIGHT)

이진트리를 배열로 표현하기

놀랍게도 이진트리는 배열로 표현될 수 있고, 공간을 매우 아낄 수 있다.

1-indexed를 기준으로 설명하면,

왼쪽 자식은 2*i, 오른쪽 자식은 2*i+1로 접근할 수 있다.
부모는 i//2로 접근할 수 있다.

# node가 지칭하고 있는 구간이 [l, r]이다. 
def init(l, r, node):
    if l == r:
        tree[node] = arr[l]
        return
    mid = (l+r) // 2
    init(l, mid, node*2)
    init(mid+1, r, node*2+1)
    tree[node] = tree[node*2] + tree[node*2+1]

init(0, N-1, 1)

1-indexed이므로, node의 초깃값은 1이다!

세그먼트 트리는 완전 이진트리로 만들 수 있다

위의 트리는 0~7번, 8개의 수를 표현한다.
만약 9개의 수를 표현하려면 어떻게 할까?

7번 노드를 갈라서 [7-7을 [7-8]로 만들고 그 자식에 7, 8번 노드를 놓을 수도 있겠다.
하지만 0번 노드를 갈라서 [0-0]을 [0-1]로 만들고 그 자식에 0, 1번 노드를 놓을 수도 있다.

후자의 방법처럼 왼쪽부터 자식을 채워넣는 트리를 완전 이진트리(Complete Binary Tree)라고 한다.
(포화 이진트리(Perfect Binary Tree)는 한 층의 자식이 모두 차있어야 하므로 개념이 다르다.)

구현

# Using Segment Tree

import sys
input = lambda: sys.stdin.readline().rstrip()
from math import ceil, log

N, M, K = map(int, input().split())
arr = []
for _ in range(N):
    arr.append(int(input()))

H = ceil(log(N, 2)+1)
tree = [0] * (2**H)

# node가 지칭하고 있는 구간이 [l, r]이다. 
def init(l, r, node):
    if l == r:
        tree[node] = arr[l]
        return
    mid = (l+r) // 2
    init(l, mid, node*2)
    init(mid+1, r, node*2+1)
    tree[node] = tree[node*2] + tree[node*2+1]

init(0, N-1, 1)

# arr[IDX]를 DIFF만큼 변경했을 때의 tree 변경
def update(l, r, node, IDX, DIFF):
    if not (l <= IDX <= r):
        return
    tree[node] += DIFF
    if l == r:
        return
    mid = (l+r) // 2
    update(l, mid, node*2, IDX, DIFF)
    update(mid+1, r, node*2+1, IDX, DIFF)

# [LEFT, RIGHT]의 구간 합을 구함.
def interval_sum(l, r, node, LEFT, RIGHT):
    if r < LEFT or RIGHT < l: # [l, r]이 [LEFT, RIGHT]를 완전히 벗어남. 
        return 0
    if LEFT <= l and r <= RIGHT: # [l, r]이 [LEFT, RIGHT] 안에 완전히 포함됨. 
        return tree[node]
    mid = (l+r) // 2
    return interval_sum(l, mid, node*2, LEFT, RIGHT) + interval_sum(mid+1, r, node*2+1, LEFT, RIGHT)

for _ in range(M+K):
    a, b, c = map(int, input().split())
    if a == 1:
        b -= 1
        update(0, N-1, 1, b, c-arr[b])
        arr[b] = c # arr도 갱신해주는 이유는... 오로지 diff 계산할 때 필요해서
    else:
        b -= 1
        c -= 1
        print(interval_sum(0, N-1, 1, b, c))

펜윅 트리로 풀어보기

그냥 이 영상을 봐라...

세그먼트 트리보다 더 최적화된 누적 합 구하기 기법이다.
16개 숫자를 저장하려면, 세그먼트 트리는 16+8+4+2+1 = 31개의 인덱스가 필요한데,
펜윅 트리는 그냥 16개면 된다!

보다보면 굉장한 의문이 든다.

변경할 때는 뭐 세그먼트 트리랑 똑같다지만, 정보를 빼먹으면 누적 합은 어떻게 구할 건데?

1부터 B까지의 누적합 - 1부터 A-1까지의 누적합으로
[A,B]의 누적합을 구한다는 발상을 보고서는 정말 깜짝 놀랐다.

이렇게 하면 정보를 빼먹어도 되는구나!

그리고 그 연산이 0이 아닌 마지막 비트(K & -K)를 더하거나 빼면서 진행된다는 세련됨에 한번 더 놀랐다.

# Using Fenwick Tree

import sys
input = lambda: sys.stdin.readline().rstrip()

N, M, K = map(int, input().split())
arr = [0] * (N+1)
fenwick_tree = [0] * (N+1) # 1-indexed 여야 함. 

# [1, i]의 누적합
def prefix_sum(i):
    answer = 0
    while i > 0:
        answer += fenwick_tree[i]
        i -= (i & -i)
    return answer

def update(i, diff):
    while i <= N:
        fenwick_tree[i] += diff
        i += (i & -i)

def interval_sum(start, end):
    return prefix_sum(end) - prefix_sum(start-1)

for i in range(1, N+1):
    x = int(input())
    arr[i] = x
    update(i, x)
    
for i in range(M+K):
    a, b, c = map(int, input().split())
    if a == 1:
        update(b, c-arr[b])
        arr[b] = c
    else:
        print(interval_sum(b, c))