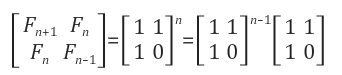
이 글은 Baekjoon, 피보나치 수를 구하는 여러가지 방법 게시글을 공부하는 용도로 작성하였습니다. 원 게시글이 C/C++로 작성되어 있어서, 필자의 코딩테스트 주력 언어인 Python으로 바꾸어보았습니다.

1단계. 일일이 호출

백준 10870. 피보나치 수 5를 풀 수 있으며, 이 문제에서는 n <= 20 이다.

n = int(input())

def fibo(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return fibo(n-1) + fibo(n-2)

print(fibo(n))

• 시간 복잡도 : O(2^N) 거의 두배씩 늘어나니까.

2단계. DP(메모이제이션)

백준 2747. 피보나치 수를 풀 수 있으며, 이 문제에서는 n <= 45 이다.

n = int(input())
dp = [0] * (45+1)

def fibo(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    if dp[n]:
        return dp[n]
    dp[n] = fibo(n-1) + fibo(n-2)
    return dp[n]

print(fibo(n))

• 시간 복잡도 : O(N) 실제 dp 계산은 한번만 하니까. 나머지는 가져다 쓴다.

3단계. DP(타뷸레이션)

백준 2748. 피보나치 수 2를 풀 수 있으며, 이 문제에서는 n <= 90 이다.

n = int(input())
dp = [0] * (90+1)
dp[1] = 1

for i in range(2, n+1):
    dp[i] = dp[i-1] + dp[i-2]
print(dp[n])

원 게시글에서는 n 값이 커지면서 자료형을 long long으로 변경해야 했지만, C와 달리 파이썬은 BigInt도 지원하기 때문에 다른 자료형을 선언할 필요 없다.

• 2단계와 3단계의 시간 복잡도는 O(N)으로 동일하기 때문에, 사실상 무슨 알고리즘을 사용하든지 통과할 수 있다.

메모이제이션과 타뷸레이션은 DP(Dynamic Programming)의 대표적인 두 기법이다.

코드를 보면 직관적으로 이해할 수 있듯이, 메모이제이션은 기존 하향식 재귀 코드(1단계)에서 중복으로 계산되는 값만 제거한 하향식 다이나믹 프로그래밍 기법이며, 타뷸레이션은 for문을 사용하여 작은 값부터 계산하면서 올라가는 상향식 다이나믹 프로그래밍 기법이다.

4단계. 피사노 주기

백준 2749. 피보나치 수 3를 풀 수 있으며, 이 문제에서는 n <= 1,000,000,000,000,000,000이지만 1,000,000으로 나눈 나머지라는 조건이 있다.

n = int(input())
dp = [0] * (1500000)
dp[1] = 1

for i in range(2, 1500000):
    dp[i] = dp[i-1] + dp[i-2]
    dp[i] %= 1000000

print(dp[n%1500000])

피보나치 수를 K로 나눈 나머지는 항상 주기를 가지게 됩니다. 이를 피사노 주기(Pisano Period)라고 합니다.

나머지 = 10^k 일 때, k > 2 라면, 주기는 항상 15 × 10^(k-1) 입니다. 이 사실을 모른다고 해도, 주기를 구하는 코드를 이용해서 문제를 풀 수 있습니다.

위 문제에 피사노 주기를 적용하면 다음과 같다.

1. 피보나치 수를 10^6으로 나눈 나머지는 주기가 15*(10^5) = 1500000이다.

2. 주기의 길이가 1500000이므로,
   N번째 피보나치 수 % 1000000 == N%1500000번째 피보나치 수 % 1000000이다.

5단계. 행렬과 분할정복

나머지가 커지면 dp 배열의 len도 커져야 하기 때문에, 피사노 주기에도 한계가 있다.

백준 11444. 피보나치 수 6를 풀 수 있으며, 이 문제에서는 n <= 1,000,000,000,000,000,000로 위 문제와 같지만, 1,000,000,007으로 나눈 나머지라는 조건에서 위의 dp 배열보다 1,000배 더 긴 배열을 선언해야 하며, 메모리 제한에 걸리기 때문에 피사노 주기를 사용할 수 없다.

이런 식이 나오게 된 과정은 다음과 같다.

1) iteration으로 분할 정복

원 게시글의 코딩 방식이 이 방식이다.

import copy

n = int(input())

def matrix_mul(A, B):
    C = [[0] * len(B[0]) for _ in range(len(A))]
    for i in range(len(C)):
        for j in range(len(C[0])):
            for k in range(len(A[0])):
                C[i][j] += A[i][k] * B[k][j]
            C[i][j] %= 1_000_000_007
    return C

if n == 0:
    print(0)
    exit()

rv = [[1, 0], [0, 1]]
a = [[1, 1], [1, 0]]
while n:
    if n%2 == 1:
        rv = matrix_mul(rv, a)
    a = matrix_mul(a, a)
    n //= 2

print(rv[0][1])

2) recursion으로 분할 정복

분할 정복은 보통 recursion을 이용하여 짜기 마련이기 때문에,
recursion을 이용하여 가독성을 높인 코드를 짜보았다.

# "분할 정복을 이용한 거듭제곱"의 의미
# 2**10 == 2**5 * 2**5
# 2**11 == 2**5 * 2**5 * 2 느낌

n = int(input())

def mmul(A, B):
    C = [[0] * len(B[0]) for _ in range(len(A))]
    for i in range(len(C)):
        for j in range(len(C[0])):
            for k in range(len(A[0])):
                C[i][j] += A[i][k] * B[k][j]
            C[i][j] %= 1_000_000_007
    return C

if n == 0:
    print(0)
    exit()

def mpow(a, n):
    if n == 1:
        return a
    a = mpow(a, n//2)
    a = mmul(a, a)
    if n%2 == 1:
        return mmul(a, [[1, 1], [1, 0]])
    return a

rv = mpow([[1, 1], [1, 0]], n)
print(rv[0][1])