최단 경로 알고리즘 : 다익스트라 VS 벨만-포드 VS 플로이드-워셜

Yongjun Park·2022년 3월 27일
Shortest Pathpython백준
0

PS(Problem Solving)

목록 보기
13/31

들어가며

솔브닥 CLASS 3에서는 그리디 알고리즘, DFS & BFS, 초급 다이나믹 프로그래밍이 핵심 알고리즘으로 사용되었으며, 이 알고리즘들은 나동빈님의 유명한 영상인 <대기업 IT직군 코딩테스트 합격을 위한 현실적이고 직관적인 공부 순서>의 중반부에서도 코딩테스트를 본격적으로 준비하는 사람에게 위의 세 알고리즘부터 풀 것을 추천하고 있다.

현재 CLASS 3의 문제들을 다 풀고 나서, 특히 상대적으로 부족하다고 생각이 들었던 초급 다이나믹 프로그래밍 카테고리의 문제들과 CLASS 4의 문제들을 병행해서 풀고 있는 상태다. CLASS 4에는 비교적 알고리즘을 떠올리기 쉬운 CLASS 3의 연장선 격의 문제들도 있는 반면, 아예 알고리즘 구현 자체가 어색해서 풀지 못하는 문제들도 있는데, 아무래도 가장 큰 난관은 최단 경로 알고리즘이었다.

이전에 자료구조와 알고리즘을 공부했을 때의 최단 경로 알고리즘은 단순히 코드를 눈으로 이해하고 넘어가봤자 빡코딩 시작하면 머리를 백지 상태로 만드는 대표적인 유형이었다. 지금 시점에서 최단 경로 알고리즘을 확실히 정리하고, 구체적인 적용 방식을 한번에 비교하면서 짚고 넘어가는 것이 앞으로 알고리즘 문제 풀이 실력을 향상하는 데 있어 꼭 필요하다는 생각에서 이 글을 쓰게 되었다.

알고리즘 별 문제 유형 예시

다익스트라 : 1753. 최단경로

방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.

예제 입력

5 6			# 정점 개수, 간선 개수
1			# 시작 정점 번호
5 1 1		# 5->1을 1의 비용으로 가는 간선 존재
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6

예제 출력

0			# 1->1 자기 자신
2			# 2->1
3			# 3->1
7			# 4->1
INF			# 5->1 이동 불가

벨만-포드 : 1865. 웜홀

때는 2020년, 백준이는 월드나라의 한 국민이다. 월드나라에는 N개의 지점이 있고 N개의 지점 사이에는 M개의 도로와 W개의 웜홀이 있다. (단 도로는 방향이 없으며 웜홀은 방향이 있다.) 웜홀은 시작 위치에서 도착 위치로 가는 하나의 경로인데, 특이하게도 도착을 하게 되면 시작을 하였을 때보다 시간이 뒤로 가게 된다. 웜홀 내에서는 시계가 거꾸로 간다고 생각하여도 좋다.

시간 여행을 매우 좋아하는 백준이는 한 가지 궁금증에 빠졌다. 한 지점에서 출발을 하여서 시간여행을 하기 시작하여 다시 출발을 하였던 위치로 돌아왔을 때, 출발을 하였을 때보다 시간이 되돌아가 있는 경우가 있는지 없는지 궁금해졌다. 여러분은 백준이를 도와 이런 일이 가능한지 불가능한지 구하는 프로그램을 작성하여라.

예제 입력

2			# 테스트케이스 개수
3 3 1		# 지점의 수, 도로의 수, 웜홀의 수
1 2 2		# 1<->2를 2의 비용으로 가는 도로
1 3 4
2 3 1
3 1 3		# 3->1을 -3의 비용으로 가는 웜홀
3 2 1		# 두번째 테스트 케이스의 지점의 수, 도로의 수, 웜홀의 수
1 2 3
2 3 4
3 1 8

예제 출력

NO
YES

플로이드-워셜 : 11403. 경로 찾기

가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.

예제 입력 1, 2

3
0 1 0
0 0 1
1 0 0
7
0 0 0 1 0 0 0
0 0 0 0 0 0 1
0 0 0 0 0 0 0
0 0 0 0 1 1 0
1 0 0 0 0 0 0
0 0 0 0 0 0 1
0 0 1 0 0 0 0

예제 출력 1, 2

1 1 1
1 1 1
1 1 1
1 0 1 1 1 1 1
0 0 1 0 0 0 1
0 0 0 0 0 0 0
1 0 1 1 1 1 1
1 0 1 1 1 1 1
0 0 1 0 0 0 1
0 0 1 0 0 0 0

한번 정리해보자.
어떤 상황에서 어떤 알고리즘을 써야 할까?

  1. 한 정점에서 다른 모든 정점까지의 최단 경로를 알고 싶다.
    1. 가중치(비용) 중에 음수는 없다. -> 다익스트라
    2. 가중치(비용) 중에 음수가 있다. -> 벨만-포드
  2. 모든 정점에서 다른 모든 정점까지의 최단 경로를 알고 싶다. -> 플로이드-워셜

그런데 가만히 생각해보면, 우리 생활에서의 문제는 보통 출발지부터 목적지까지 가는 데 걸리는 최소비용에 대하여 발생한다.

그리고 음수 비용이 있다는 말은, 위의 벨만-포드 알고리즘 예시에서도 나왔지만 웜홀과 같이, 드는 시간을 오히려 역행해주는 뭔 말도 안되는 예시가 나와야 된다.

따라서, 대부분의 최단경로 문제는 다익스트라 알고리즘으로 푸는 것이 default라고 생각해두고 있으면 된다.

1. 다익스트라(Dijkstra)

설명

한 단계를 거칠 때마다 최단 거리 하나, 즉 특정 정점 하나까지의 최단거리는 확정되어 미래에도 절대 바뀌지 않는다.

(최솟값 또는 최댓값 하나만을 확정하면서 정렬해나가는 선택 정렬Selection sort 이 주는 느낌과 매우 흡사하다.)

(또한, 현재 상태에서 그나마 최단거리인 걸 하나씩 정복해나간다는 점에서 그리디 알고리즘의 성질을 가진다.)

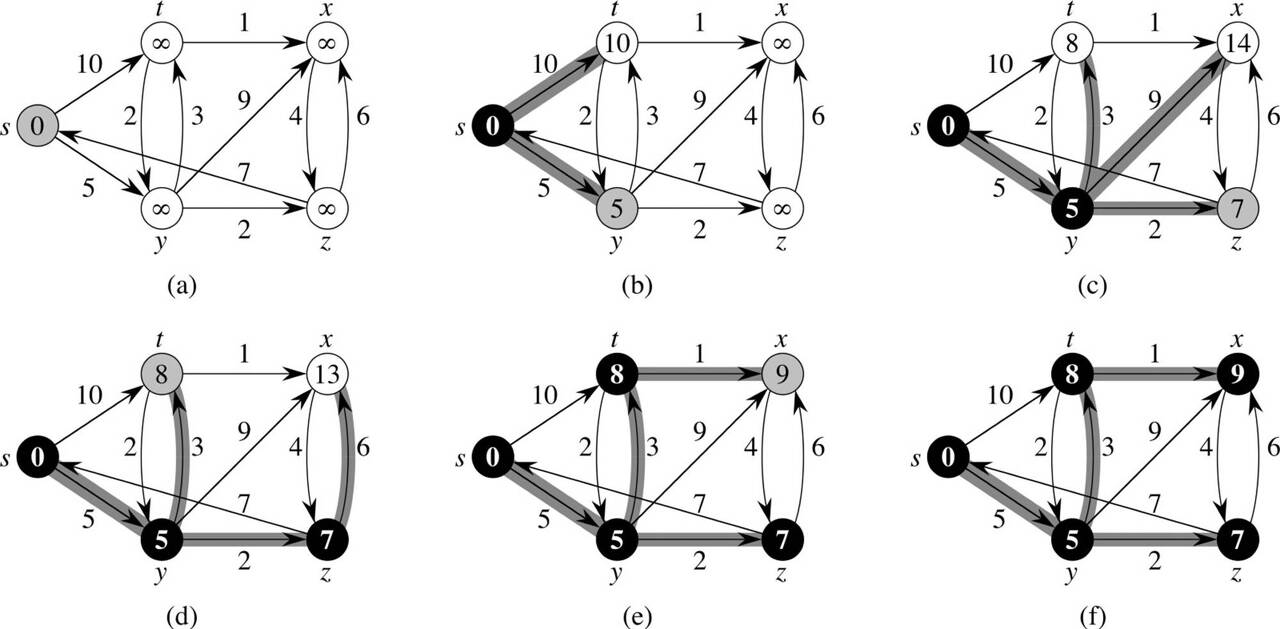
(a)에서 (f)에 이르는 과정을 꽤 시간을 들여 살펴보자.

  • 하얀색은 아직 도달해보지도 못한 정점
  • 회색은 인접 노드 덕분에 도달할 수 있게 되어 리스트에 들어간 정점
  • 검은색은 리스트에 있는 정점 중 가장 비용이 적어 현재 방문하고 있거나, 이미 방문한 정점이다.

동작 과정

  1. 현재 선택한 정점(처음엔 시작점)에 곧장 연결되고, 아직 방문하지 않은 정점들을 모두 본다.
  2. 시작 정점과 선택한 정점까지의 최단거리와 선택한 정점과 보고있는 정점 사이의 거리의 합이 현재까지 구한 시작 정점과 보고 있는 정점 사이의 거리보다 짧을 경우, 이를 갱신해준다.
  3. 1, 2번 수행이 모두 끝난 이후, 아직 방문하지 않은 정점들 중 시작점과의 거리가 가장 짧은 정점을 선택한다.
  4. 방문하지 않은 정점이 존재하여 정점을 선택했다면, 현재 구한 시작점으로부터의 현재 선택한 정점 사이의 거리는 최단거리이다.
  5. 방문하지 않은 정점이 존재하지 않는다면, 수행을 종료한다. 그렇지 않으면 1번으로 돌아가 수행을 반복한다.

시간 복잡도

  • 기본적으로 O(n^2)이다. not visited 상태인 정점을 순회하므로 기본적으로 O(n)이고, 그 정점을 고르는 과정 중에 리스트 내에 있는 간선들 중 최소 비용인 것을 순회 비교하면서 골라야하기 때문에 여기서 또 O(n)이 든다.
    (뭐 엄밀히 말하면, 정점의 개수를 E(Edge), 간선의 개수를 V(Vertex)라고 했을 때 O(E*V)가 든다고 할 수 있겠다.)

  • 하지만 최소 비용을 매번 고르는게 비효율적이라는 생각이 들지 않는가? (같은 일을 여러번 하고 있다는 생각이 들어야 한다...)

  • 그 리스트를 힙(Heap)으로 만들면 매우 파격적으로 시간복잡도를 줄일 수 있다. 해당 정점까지 걸리는 비용을 기준으로 python의 heapq.heappush를 이용하면 삽입하는데 O(logn), 찾는데는 O(1)(추출하는 데는 힙을 재배치하는 비용이 들기 때문에 O(logn))이 들게 만들 수 있다.
    따라서 리스트를 힙으로 구현한다면 시간복잡도는 O(nlogn)으로 줄어든다. 이것 역시 엄밀히 말하면 O(ElogV)겠지만...

구현(Python)

Method 1. O(n^2) 방식

Method 1은 이해 안 되면 대충 보고 넘어가도 된다.
어차피 중요한건 힙을 사용하는 Method 2니까. 

import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 방문한 적이 있는지 체크하는 목적의 리스트를 만들기
visited = [False] * (n + 1)
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)

# 모든 간선 정보를 입력받기
for _ in range(m):
    a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미
    graph[a].append((b, c))

# 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
def get_smallest_node():
    min_value = INF
    index = 0 # 가장 최단 거리가 짧은 노드(인덱스)
    for i in range(1, n + 1):
        if distance[i] < min_value and not visited[i]:
            min_value = distance[i]
            index = i
    return index

def dijkstra(start):
    # 시작 노드에 대해서 초기화
    distance[start] = 0
    visited[start] = True
    for j in graph[start]:
        distance[j[0]] = j[1]
    # 시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
    for i in range(n - 1):
        # 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
        now = get_smallest_node()
        visited[now] = True
        # 현재 노드와 연결된 다른 노드를 확인
        for j in graph[now]:
            cost = distance[now] + j[1]
            # 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[j[0]]:
                distance[j[0]] = cost

# 다익스트라 알고리즘을 수행
dijkstra(start)

# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
    # 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
    if distance[i] == INF:
        print("INFINITY")
    # 도달할 수 있는 경우 거리를 출력
    else:
        print(distance[i])

Method 2. O(nlogn) 방식

아래 코드의 dijkstra 함수 부분은 진짜 의식의 흐름대로 칠 정도로 달달 외워라.

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)

n, m = map(int, input().split())
start = int(input())
graph = [[] for i in range(n + 1)]
visited = [False] * (n + 1)
distance = [INF] * (n + 1)

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))

def dijkstra(start):
    q = []
    # 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
    heapq.heappush(q, (0, start))
    distance[start] = 0
    while q: # 큐가 비어있지 않다면
        # 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
        dist, now = heapq.heappop(q)
        # 현재 노드가 이미 처리된 적이 있는 노드라면 무시
        if distance[now] < dist:
            continue
        # 현재 노드와 연결된 다른 인접한 노드들을 확인
        for i in graph[now]:
            cost = dist + i[1]
            # 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))

dijkstra(start)

for i in range(1, n + 1):
    if distance[i] == INF:
        print("INFINITY")
    else:
        print(distance[i])

참고로, graph는 (정점 번호, 비용) 순으로 입력이 들어가는 반면, heap에는 (비용, 정점 번호) 순으로 들어가는 것을 주의해야 한다. 따라서

  1. 예전에 heap에 들어왔던 간선이라도 최근에 들어온 간선이 더 비용이 적어 먼저 선택되는 것이 가능하며,
  2. 계속 도태되는 비용을 가진 간선은 계속 밀려나다가 나중에 다 최적화되고 나서야 heap에서 선택이 되는데, 그때는 이미 distance[now] < dist 상태일 것이다. 해당 조건은 이런 도태된 간선들을 위해 존재한다.

2. 벨만-포드(Bellman-Ford)

Q. 다익스트라에 음수 비용이 들어가면 뭐가 문젠데?

어차피 비용 최솟값 갱신하는 건 마찬가지고 heapq가 지원하는 최소 힙이 음수를 받지 않는 것도 아니고, 음수를 문제시할 필요가 없지 않은가...라는 생각이 분명히 들 수 있다.

하지만 위의 다익스트라 알고리즘에 다음 두 개의 테스트 케이스를 넣어보자.

예제 입력 1

5 8
1
1 2 -1
1 3 4
2 3 3
2 4 2
2 5 2
4 2 1
4 3 5
5 4 -3

예제 입력 2

5 9
1
1 2 -1
1 3 4
2 3 3
2 4 2
2 5 2
3 1 -5
4 2 1
4 3 5
5 4 -3

예제 입력 1, 2는 다음과 같은 출력을 내보낸다.

예제 출력 1

0
-1
2
-2
1

오, 뭔가 음수도 되는거 같은데?

하지만 예제 입력 2를 넣으면 무한루프에 빠져 프로그램이 종료되지 않는다.

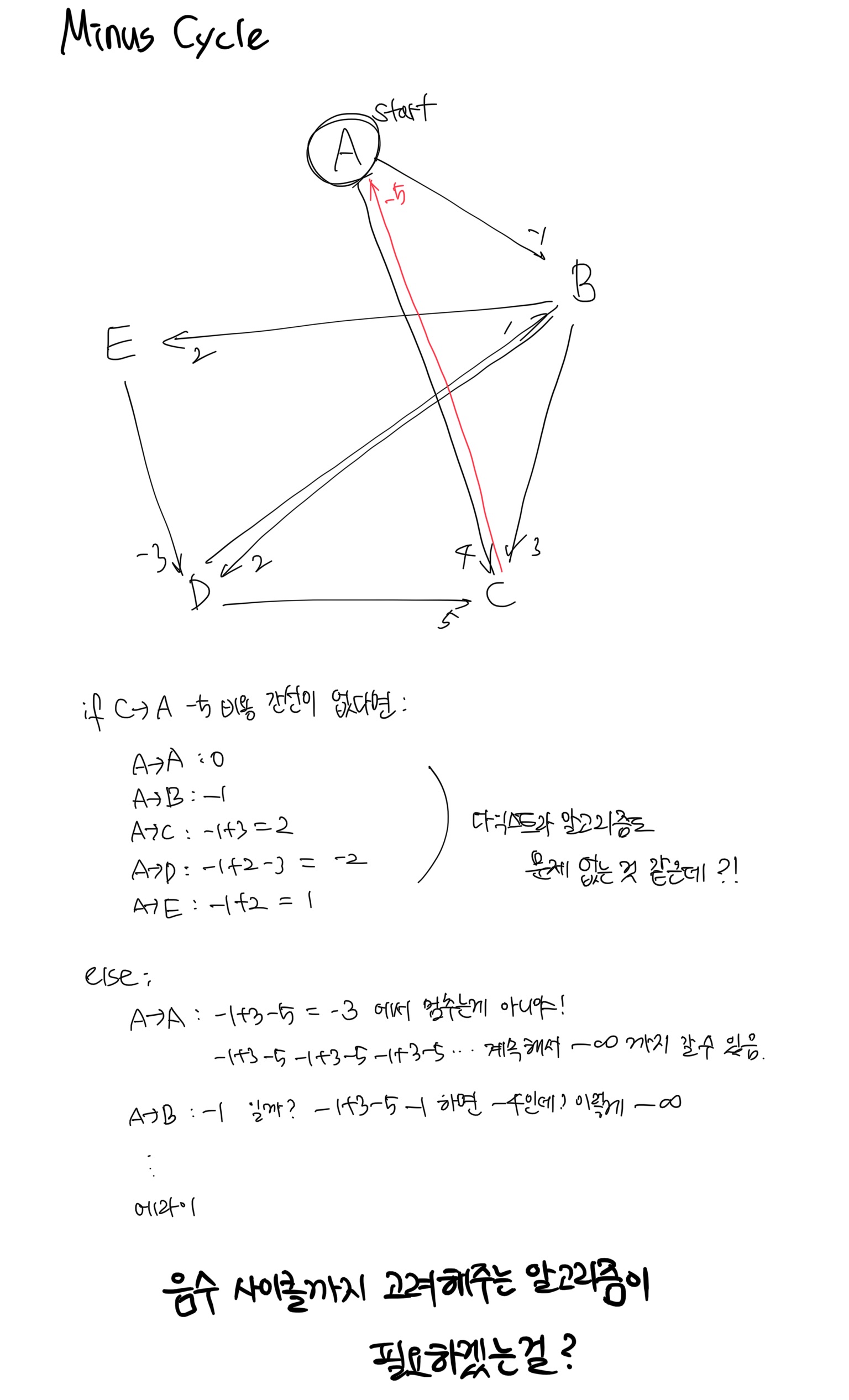
와! 정말 필요하겠는걸?

한 마디로 표현하자면, 벨만-포드 알고리즘은 다익스트라 알고리즘보다 시간은 오래 걸릴지언정 음수 간선 순환은 탐지할 수 있는 알고리즘이다.

동작 과정

편의를 위해 graph는 dictionary를 담은 dictionary로 설정한다.
(이후 tuple을 담은 dictionary로 코드 개선 요망)

  1. 모든 정점으로 가는 비용을 INF로 설정한다.
  2. 시작점은 비용을 0으로 설정한다.
  3. 그래프의 모든 정점을 순회하면서 for node in graph
    1. 나의 모든 인접 정점에 대하여 for neighbour in graph[node]
    2. 지금 인접 정점에 써있는 비용보다 나를 거쳐가는게 더 싸다면
    3. 인접 정점의 비용을 개선한다.
  4. 3번의 행동을 정점의 개수(V) - 1만큼 반복한다.
  5. 그 다음 3번의 행동을 한번 더하는데, 아직도 그래프가 개선되는 상황이 발생한다면 그건 진짜 개선이 아니라 음수 사이클로 판별하고 함수를 종료한다. 바뀌지 않는다면 이미 최단 경로를 구한 것이므로 그대로 반환한다.

왜 V가 아니라 V-1번이지?

처음에 시작점의 비용을 0으로 설정하면,
이미 하나가 확정된 상황이기 때문에 한번 덜 해도 된다는 것이다.

예를 들어, a->b->c->d->e->f인 그래프를 보도록 하자.
모든 가중치가 1이라고 한다면, 시작했을 땐 [0, INF, INF, INF, INF, INF]일 것이다.

그 다음에는 다음과 같이 변한다.

  • 1회차 : [0, 1, INF, INF, INF, INF]
  • 2회차 : [0, 1, 2, INF, INF, INF]
  • 3회차 : [0, 1, 2, 3, INF, INF]
  • 4회차 : [0, 1, 2, 3, 4, INF]
  • 5회차 : [0, 1, 2, 3, 4, 5]

음수 사이클이 없는 상황이라면, 굳이 6회차를 할 필요가 없다.

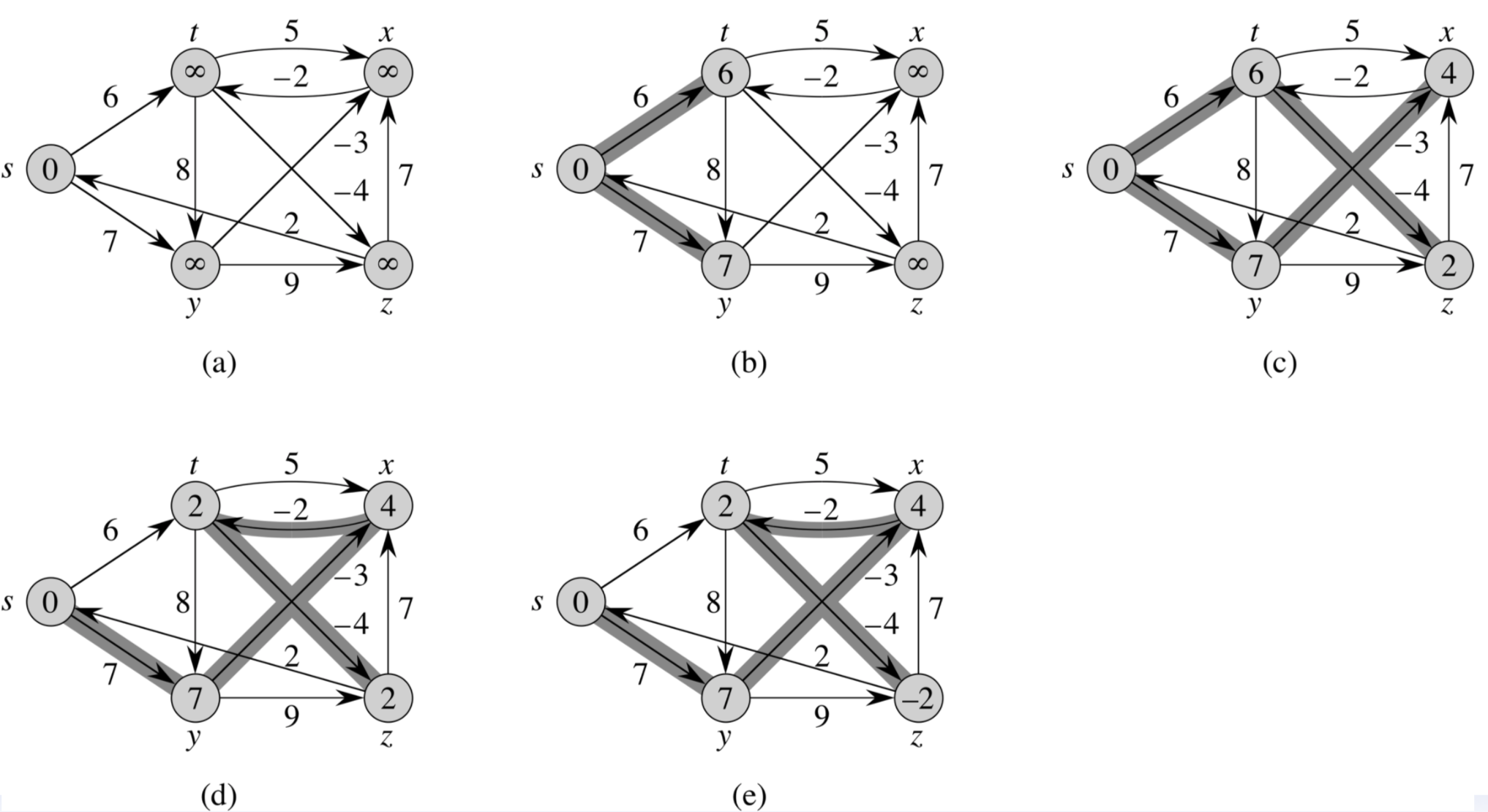
아니, 음수 가중치가 있다면 위의 상황처럼 정점이 재갱신되는 듯한 상황도 있는 거 같은데?

라는 생각이 들 수도 있겠지만, 다시 침착하게 생각해보면 이 역시 V-1번 이상으로 나올 수가 없다는 것을 알 수 있다.

위에서 z 정점까지의 최단거리는 s->y->x->t->z라는 매우 복잡한 경로로 결정되는데, 이것 역시 4번이면 확정된다.

이왜진

재갱신에 대하여

  1. 음수 사이클인 경우의 재갱신
    만약 s와 붙어있는 정점인 t나 y가 6과 7보다 더 낮은 최단거리를 갖는 것으로 재갱신된다면, 다시 그 상태로 V-1번을 또 돌려야 되는, 즉 수포로 돌아가는 것이 아닐까 생각할 수도 있다.
    하지만 이런 경우는 음수 사이클이기 때문에 무시해도 된다.

  2. 음수 사이클이 아닌 경우의 재갱신
    (d)번에서 t가 6에서 2로 재갱신되고, (e)번에서 z가 2에서 -2로 재갱신된 이유는, 음수 사이클이 존재해서가 아니라 x->t -2 간선이 (d)번에서 처음 발견되었기 때문이며(x=4가 (c)에서 처음 확정되었기에 (d)에서 해당 간선을 처음 보게 되는 것이다), 덕분에 t로 가는게 s->t 경로보다 s->y->x->t 경로가 더 싸다는 것을 알게 되었고, 그래서 재갱신되는 것뿐이다.

구현(Python)

이 구현은 대충 보고 넘어가도 된다.
어차피 중요한건 아래 구현이다. 

def bellman_ford(graph, start):
    distance, predecessor = dict(), dict()  # 거리 값, 각 정점의 이전 정점을 저장할 딕셔너리
    # 거리 값을 모두 무한대로 초기화 / 이전 정점은 None으로 초기화
    for node in graph:  
        distance[node], predecessor[node] = float('inf'), None
    distance[start] = 0  # 시작 정점 거리는 0

    # V-1만큼 반복
    for _ in range(len(graph) - 1):
        for node in graph:
            for neighbour in graph[node]:  # 각 정점마다 모든 인접 정점들을 탐색
                # (기존 인접 정점까지의 거리 > 기존 현재 정점까지 거리 + 현재 정점부터 인접 정점까지 거리)인 경우 갱신
                if distance[neighbour] > distance[node] + graph[node][neighbour]:
                    distance[neighbour] = distance[node] + graph[node][neighbour]
                    predecessor[neighbour] = node

    # 음수 사이클 존재 여부 검사 : V-1번 반복 이후에도 갱신할 거리 값이 존재한다면 음수 사이클 존재
    for node in graph:
        for neighbour in graph[node]:
            if distance[neighbour] > distance[node] + graph[node][neighbour]:
                return -1, "그래프에 음수 사이클이 존재합니다."

    return distance, predecessor


# 음수 사이클이 존재하지 않는 그래프
graph = {
    'A': {'B': -1, 'C':  4},
    'B': {'C':  3, 'D':  2, 'E':  2},
    'C': {},
    'D': {'B':  1, 'C':  5},
    'E': {'D': -3}
}

# 그래프 정보와 시작 정점을 넘김
distance, predecessor = bellman_ford(graph, start='A')

print(distance)
print(predecessor)


# 음수 사이클이 존재하는 그래프
graph = {
    'A': {'B': -1, 'C':  4},
    'B': {'C':  3, 'D':  2, 'E':  2},
    'C': {'A': -5},
    'D': {'B':  1, 'C':  5},
    'E': {'D': -3}
}

print('----------')

distance, predecessor = bellman_ford(graph, start='A')

print(distance)
print(predecessor)

distance와 predecessor에는 각각 무엇이 들어가는가?

위의 코드의 출력을 보면 알 수 있다.

distance는 다익스트라에서와 마찬가지로 최소비용 값이 들어가 있고,
predecessor에는 최소비용으로 갈 때의 자신의 이전 정점이 들어가 있다.

덕분에 최소비용으로 가는 경로를 역추적해나갈 수 있겠다.
예를 들어, E로 가는 최단 경로를 알고 싶다면 E <- B <- A라고 깨달을 수 있다.

구현(2022.03.28. 추가)

자료구조의 통일성을 위해 기존 사용하던 defaultdict(list)에 (도착점, 가중치) 튜플을 담아 사용하는 예시를 직접 구현하여 추가한다.

아래 코드의 bellman_ford 함수 부분은 진짜 의식의 흐름대로 칠 정도로 달달 외워라. 

import sys
from collections import defaultdict
INF = int(1e9)

# V = Vertex(정점), E = Edge(간선)
V, E = map(int, sys.stdin.readline().rstrip().split())
start = int(sys.stdin.readline().rstrip())
graph = defaultdict(list)
for _ in range(E):
    a, b, c = map(int, sys.stdin.readline().rstrip().split())
    graph[a].append((b, c))

dist = [INF] * (V+1) # dist[0]은 안 씀

def bellman_ford(start):
    dist[start] = 0
    for _ in range(V-1):
        for i in range(1, V+1):
            for node, weight in graph[i]:
                dist[node] = min(dist[node], dist[i]+weight)

    for i in range(1, V+1):
        if dist[node] > dist[i]+weight:
            return False
    return True
            
have_minus_cycle = bellman_ford(start)
if have_minus_cycle:
    print('음수 사이클이 있습니다.')
else:
    print(dist[1:])

3. 플로이드-워셜(Floyd-Warshall)

설명

필자가 쓴 [오답노트] 백준 #11403 경로 찾기 (파이썬)
 글을 읽어보면 플로이드-워셜 알고리즘의 느낌을 이해할 수 있다.

위 글의 결론부에서도 이미 말했지만, 

for k in range(N):
    for i in range(N):
        for j in range(N):
            if graph[i][k] and graph[k][j]:
                graph[i][j] = 1
for k in range(N):
    for i in range(N):
        for j in range(N):
            if graph[i][k] + graph[k][j] < graph[i][j]:
                graph[i][j] = graph[i][j] + graph[k][j]

위의 코드를 아래의 코드처럼 조건문만 바꾸면,
모든 정점과 모든 정점 사이의 최단 경로를 구해준다.

시간 복잡도

아... for문 3개에서 이미 짐작하셨다시피 O(n^3)이다.

그래서 정점의 개수가 500개 이하인 경우가 대부분이다.
(1000개만 되도 1000*1000*1000 = 10억이기 때문에)

문제를 풀 때, 정점의 개수가 100개와 같이 티날 정도로 적다면 플로이드 워셜을 의심해보자.

구현(Python)

INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0

# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
    # A에서 B로 가는 비용은 C라고 설정
    a, b, c = map(int, input().split())
    graph[a][b] = c

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

# 수행된 결과를 출력
for a in range(1, n + 1):
    for b in range(1, n + 1):
        # 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
        if graph[a][b] == 1e9:
            print("INFINITY", end=" ")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(graph[a][b], end=" ")
    print()

눈으로 보고만 넘기지 말고,
반드시 직접 한번 자신의 언어로 구현해보고,
가능하면 외울 정도로 반복하자.

Reference

profile
Yongjun Park
추상화되었던 기술을 밑단까지 이해했을 때의 쾌감을 잊지 못합니다
이전 포스트

[오답노트] 백준 #1629 곱셈 (파이썬) : 나머지 연산의 분배법칙

다음 포스트

다익스트라, 벨만-포드, 플로이드-워셜 함수 핵심부만 모아보기

0개의 댓글