
📎벡터가 뭐예요?
벡터란?
숫자를 원소로 가지는 리스트(list) 또는 배열(array)
또는
공간에서 한 점으로, 원점으로부터의 상대적 위치
특징
- 벡터에 숫자를 곱하면 길이만 변한다.
- 같은 모양을 가지면 덧셈, 뺄셈과 성분곱을 계산할 수 있다.
벡터의 노름
원점에서부터의 거리
L1-norm
각 성분의 변화량의 절대값을 모두 더한다.
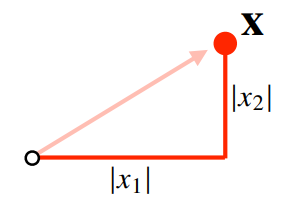
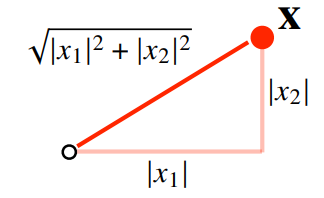
L2-norm
피타고라스 정리를 이용해 유클리드 거리를 계산한다.
파이썬 코드
def l1_norm(x):
x_norm = np.abs(x)
x_norm = np.sum(x_norm)
return x_norm
def l2_norm(x):
x_norm = x*x
x_norm = np.sum(x_norm)
x_norm = np.sqrt(x_norm)
return x_norm백터의 내적
벡터 x의 정사영 길이를 백터 y의 길이만큼 조정한 값
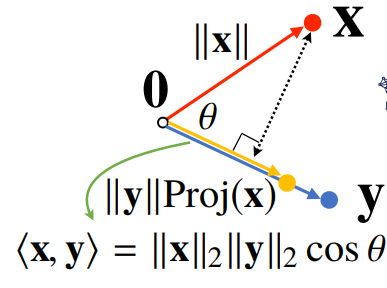
두 벡터의 유사도(similarity)를 측정하는데 사용 가능하다
📐행렬이 뭐예요?
행렬이란?
벡터를 원소로 가지는 2차원 배열
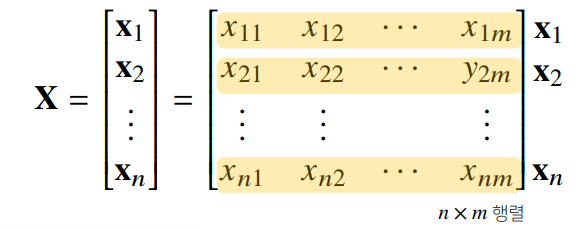
특징
- 행(row)과 열(column)이라는 인덱스(index)를 가진다.
- 행렬은 대문자 X, 벡터는 소문자 x로 표현한다.
벡터가 공간에서 한 점을 의미한다면 행령은 여러 점들을 나타낸다.
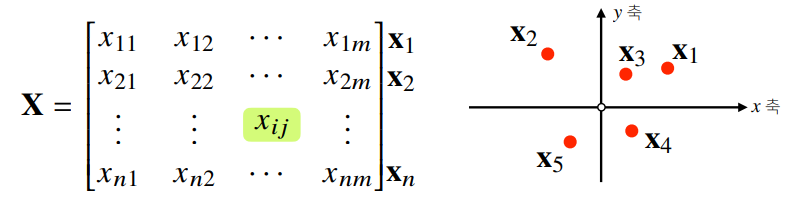
행렬의 는 번째 데이터의 번째 변수의 값을 말한다
- 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다.
- 성분곱과 스칼라곱도 벡터와 차이가 없다.
행렬의 곱셈(matrix multiplication)
번째 행벡터와 번째 열벡터 사이의 내적을 성분으로 가지는 행렬 계산
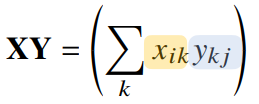
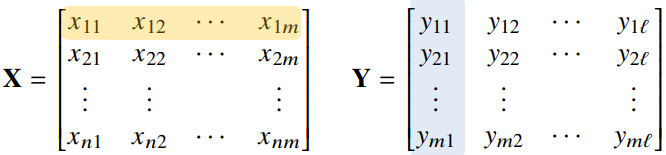
X의 열의 개수와 Y의 행의 개수가 같아야 한다.
행렬도 내적이 있을까?
- numpy의 np.innner는 번째 행벡터와 번째 행벡터 사이의 내적
- 수학에서 말하는 내적과는 다르다!
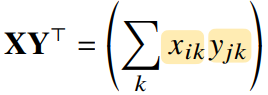
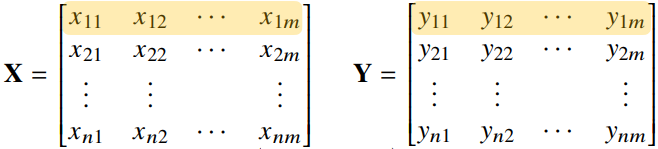
※ 전치행렬이란?
행과 열의 인덱스가 바뀐 행렬

파이썬 코드
X = np.array([])
Y = np.array([])
# numpy에서 @ 연산을 사용한다
X @ Y
# 내적
np.inner(X,Y)행렬을 이해하기
벡터공간에서 사용되는 연산자(operator)로 이해
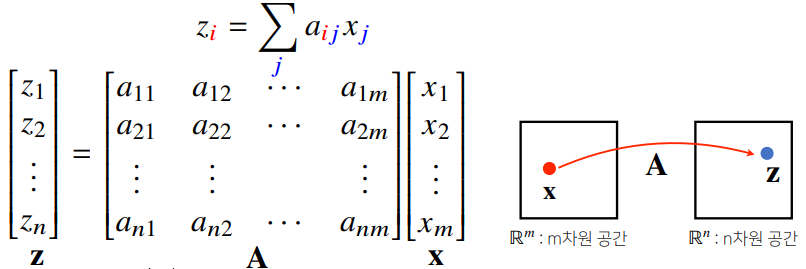
행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다 → 패턴 추출, 데이터 압축 가능!
역행렬
어떤 행렬의 연산을 거꾸로 되돌리는 행렬
- 계산 조건
1. 행과 열 숫자가 같다.
2. 행렬식이 0이 아니다.
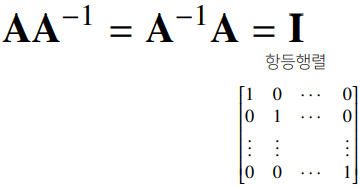
파이썬 코드
X = np.array([])
np.linalg.inv(X)
# 항등행렬이 나오는데 0은 아니지만 가까운 숫자로 나온다
X @ np.linalg.inv(X) 역행렬을 계산할 수 없다면?
유사역생렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose)역행렬을 이용
행의 개수(n)가 많을 경우와 열의 개수(m)가 많을 경우 다르게 계산
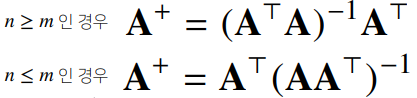
※ 는 역행렬이 계산이 되는 행렬!
Y = np.array([])
np.linalg.pinv(Y)응용1: 연립방정식 풀기
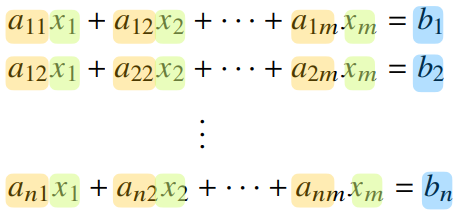
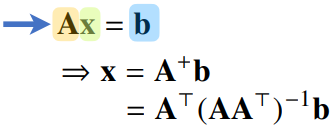
응용2: 선형회귀분석
데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있다
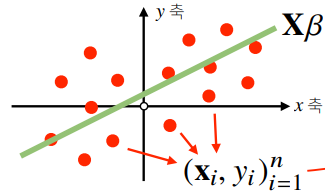
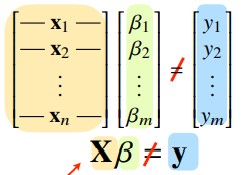
선형회귀분석은 연립방정식과 달리 행이 더 크므로 방정식으로 푸는건 불가능
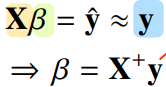
에 근접한 를 찾는다!
L2-노름을 최소화! →
- sklearn의 LinearRegression을 사용
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X,y)
y_test = model.predict(x_test)moore-penrose을 사용하려면 y절편항을 더해줘야된다.
