문제 요약
문제 요약
골드바흐 파티션의 개수를 찾는 문제이다.
골드바흐 파티션 : 짝수 N을 두 소수의 합으로 나타내는 표현
입력
첫째줄 : Testcase 수
2 ~ T+1번째 줄 : 각 Testcase
출력
각 Testcase의 골드바흐 파티션 수
풀이
여러 Testcase의 짝수의 모든 골드바흐 파티션을 구해야 한다.
골드바흐 파티션은 소수의 합으로 표현하는 것이므로 소수들을 미리 구할 필요가 있다.
한 소수를 찾는 방법은 N을 입력 받고 root(N)까지 나눠지는지 확인하는 방식이 있지만 우리는 골드바흐 파티션을 구하기 위해 수 많은 소수를 찾아야 한다.
여러개의 소수를 구하려면?
에라토스테네스의 체 방식을 쓰면 된다.
prime = [True] * (N+1)
prime[0] = False; prime[1] = False
for i in range(2, max_N+1):
if prime[i] == True:
j = 2
while i*j <= max_N:
prime[i*j] = False
j += 1이 방식으로 N 이하의 모든 소수를 빠르게 구할 수 있다.
골드바흐 파티션 수는 어떻게 구할까?
Testcase마다 소수 목록을 for문으로 돌리면서 Testcase - 소수가 소수인지 확인하고 count를 +1 해주면 된다.
for num in N:
cnt = 0
for a in prime_list:
if prime[num-a] == True:
cnt += 1
print(cnt)시간 초과가 되지 않으려면 신경써야 할 부분
- 소수를 구할 때 에라토스테네스의 체 방식을 써야한다.
- 소수만 따로 모아둔 리스트를 활용하여 'Testcase - 소수'가 소수인지 판별해야 한다.
결과 코드
import sys
input = sys.stdin.readline
T = int(input()); N = []
for i in range(T):
N.append(int(input()))
max_N = max(N)
prime = [True] * (max_N+1)
prime[0] = False; prime[1] = False
prime_list = []
for i in range(2, max_N+1):
if prime[i] == True:
prime_list.append(i)
j = 2
while i*j <= max_N:
prime[i*j] = False
j += 1
for num in N:
cnt = 0
for a in prime_list:
if prime[num-a] == True and num - a >= a:
cnt += 1
print(cnt)마치며
생각보다 시간 초과로 애를 먹었다.
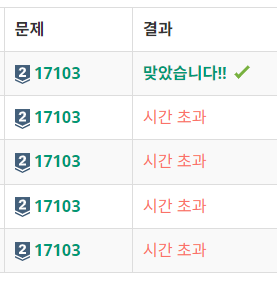
언제든 3중 for문은 피해야 하는 표현이 맞는 것 같다...
