[Python] 그리디 - 2

sliver gun·2025년 6월 1일

알고리즘 파이썬

알고리즘

목록 보기

22/30

1️⃣ BOJ 2885 - 초콜릿 식사

문제 링크

https://www.acmicpc.net/problem/2885

문제 설명

학교 근처 편의점에 새 초콜릿이 들어왔다. 이 초콜릿은 막대 모양이고, 각 막대는 정사각형 N개로 이루어져 있다. 초콜릿의 크기(정사각형의 개수)는 항상 2의 제곱 형태이다. 즉, 1, 2, 4, 8, 16, ...개의 정사각형으로 이루어져 있다.
상근이는 점심식사로 초콜릿을 먹는다. 이때, 적어도 K개 정사각형을 먹어야 남은 수업을 졸지 않고 버틸 수 있다. 상근이의 친구 선영이도 초콜릿을 좋아한다. 선영이는 초콜릿은 돈을 주고 사기 아깝다고 생각하기 때문에, 상근이가 주는 초콜릿만 먹는다.
상근이는 막대 초콜릿를 하나 산 다음에, 정확하게 K개 정사각형이 되도록 초콜릿을 쪼갠다. K개는 자신이 먹고 남는 것은 선영이에게 준다.
막대 초콜릿은 나누기 조금 어렵게 되어 있어서, 항상 가운데로만 쪼개진다. 즉, 정사각형이 D개 있는 막대는 D/2개 막대 두 조각으로 쪼개진다.
K개 정사각형을 만들기 위해서, 최소 몇 번 초콜릿을 쪼개야 하는지와 사야하는 가장 작은 초콜릿의 크기를 구하는 프로그램을 작성하시오. 상근이는 초콜릿을 하나만 살 수 있다. 꼭 한 조각이 K개일 필요는 없고, 여러 조각에 있는 정사각형을 합쳤을 때 K개이면 된다.

6칸의 정사각형을 위해선 8개 크기의 막대를 1번(4+4), 2번(4+2+2) 쪼개서 4+2를 만들어 최소 2번 쪼개면 된다.

입력

첫째 줄에 K가 주어진다. (1 ≤ K ≤ 1,000,000)

출력

첫째 줄에는 상근이가 구매해야하는 가장 작은 초콜릿의 크기와 최소 몇 번 쪼개야 하는지를 출력한다.

예시

정답

K = int(input())
i = 1
while i < K:
    i <<= 1
res = i

cnt = 0
while K > 0:
    if i > K:
        i >>= 1
        cnt += 1
    else:
        K -= i

print(res, cnt)

목표로하는 정사각형 개수 K보다 크거나 같은 최소의 2의 제곱 형태의 수 i 를 구해주고

i를 2로 나누면서 K개의 정사각형을 모아가면 된다.

i > K 일 때는 반으로 쪼개야 하므로 cnt를 1 늘리고 i를 2로 나눈다.
i ≤ K 일 때는 안 쪼개도 되므로 K에서 i 개의 정사각형만 제한다.

이런식으로 반복하면 최소 몇번 쪼개지는지 알 수 있다.

2️⃣ BOJ 3061 - 사다리

문제 링크

https://www.acmicpc.net/problem/3061

문제 설명

상덕이는 매일 점심시간마다 무엇을 먹어야 할 지 매우 고민에 빠진다. 결국 상덕이는 사다리게임을 하기로 했다. 밥을 같이 먹는 희원이는 상덕이를 놀리고 싶은 마음에, 희원이가 원하는 대로 사다리를 그리고 싶어한다.

희원이는 상덕이를 잘 속이기 위해서, 가장 적은 가로줄로 사다리를 빨리 그리려고 한다.

예를 들어, 아래와 같은 사다리를 보자. 희원이는 이 사다리의 1번 시작점은 2번째 도착점으로, 2번 시작점은 3번째 도착점으로, 3번 시작점은 1번째 도착점으로 도착하게 가로줄을 그리려고 한다. 이때, 아래 그림과 같이 두 개의 가로줄을 그리면, 희원이가 원하는 대로 사다리를 그릴 수 있고, 이것이 최솟값이 된다.

단, 희원이가 그리는 가로줄 중 같은 높이에 그리는 가로줄은 없다.

희원이가 원하는 대로 사다리를 그리는데 필요한 가로줄 개수의 최솟값을 구하는 프로그램을 작성하시오.

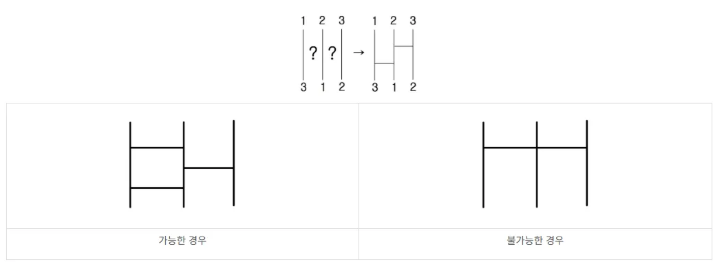
순서대로 있는 숫자를 사다리타기를 통해 특정 배열로 배치하기 위해 필요한 최소 사다리(가로줄) 수를 구하는 것!

입력

입력은 T개의 테스트 데이터로 구성된다.

입력의 첫 번째 줄에는 입력 데이터의 수를 나타내는 정수 T가 주어진다. 각 테스트 데이터는 두 줄로 구성되어 있다.

첫 번째 줄에는 사다리 세로줄의 개수 N이 주어진다.

둘째 줄에는 1번 도착점으로 도착하는 시작점의 번호, 2번 도착점으로 도착하는 시작점의 번호, …, N번 도착점으로 도착하는 시작점의 번호가 공백으로 구분되어 주어진다.

N은 1,000보다 작거나 같은 자연수이다.

출력

각 테스트 데이터에 대해, 가장 적은 가로줄의 개수를 출력한다.

예시

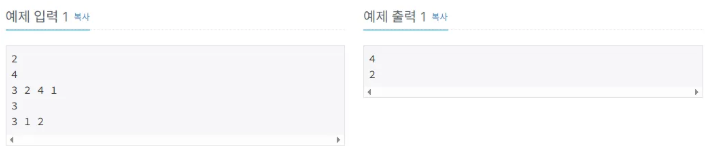
정답

def solve(l):
    cnt = 0
    for i in range(len(l)-1):
        for j in range(len(l)-1-i):
            if l[j] > l[j+1]:
                cnt += 1
                (l[j], l[j+1]) = (l[j+1], l[j])
    return cnt

for i in range(int(input())):
    n = int(input())
    l = list(map(int, input().split()))
    print(solve(l))